Khoảng cách giữa 2 đường thẳng trong không gian Oxyz là 1 dạng gây khó khăn cho nhiều học sinh khi làm bài tập. Tuy nhiên, nếu nhớ chính xác các công thức thì dạng toán này lại trở lên dễ dàng hơn

Cơ sở lý thuyết

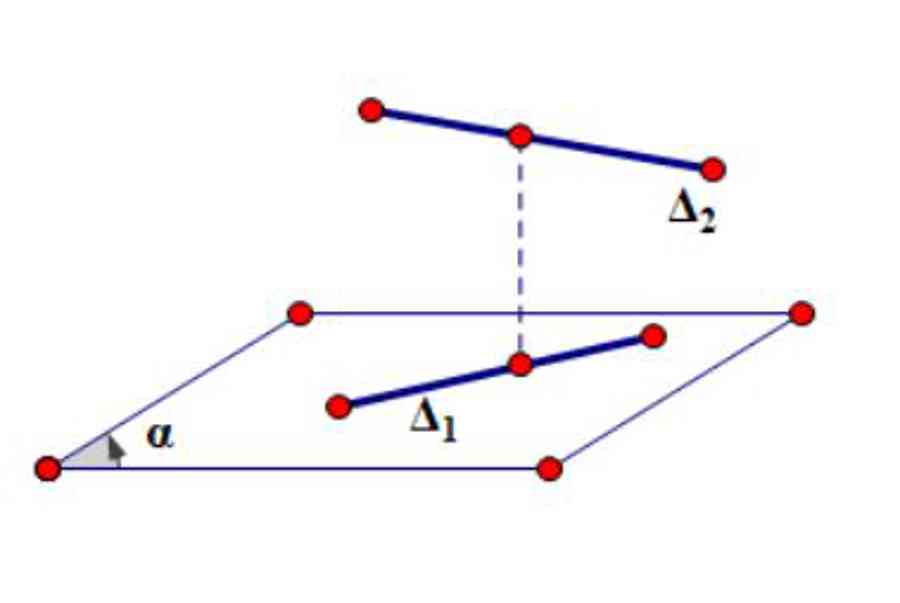
Bài toán. Trong không gian Oxyz, cho hai đường thẳng Δ1, Δ2. Hãy xác định khoảng cách giữa 2 đường thẳng này?

Hướng dẫn
Khi tính khoảng cách giữa 2 đường thẳng trong khoảng trống, ta phân làm 2 trường hợp riêng không liên quan gì đến nhau

Trường hợp 1: Nếu Δ1 //  Δ2, nghĩa là Δ1: $\left\{ \begin{array}{l} x = {x_1} + a{t_1}\\ y = {y_1} + b{t_1}\\ z = {z_1} + c{t_1} \end{array} \right.,\,\left( {{t_1} \in R} \right)$ và Δ2: $\left\{ \begin{array}{l} x = {x_2} + ka{t_2}\\ y = {y_2} + kb{t_2}\\ z = {z_2} + kc{t_2} \end{array} \right.,\,\left( {{t_2} \in R} \right)$

Từ phương trình của đường thẳng ta suy ra

• M1(x1, y1, z1) và M2(x2, y2, z2)
• Vecto chỉ phương $\overrightarrow u $ = (a; b; c)

Lúc này, công thức tính khoảng cách :
d ( Δ1, Δ2 ) = $ \ frac { { \ left | { \ overrightarrow { { M_1 } { M_2 } } \ wedge \ overrightarrow u } \ right | } } { { \ left | { \ overrightarrow u } \ right | } } $

Trường hợp 2: Nếu Δ1, Δ2 chéo nhau thì Δ1: $\left\{ {\begin{array}{*{20}{l}} {x = {x_1} + {a_1}{t_1}}\\ {y = {y_1} + {b_1}{t_1}}\\ {z = {z_1} + {c_1}{t_1}} \end{array}} \right.,{\mkern 1mu} {\kern 1pt} \left( {{t_1} \in R} \right)$ và Δ2: $\left\{ {\begin{array}{*{20}{l}} {x = {x_2} + {a_2}{t_2}}\\ {y = {y_2} + {b_2}{t_2}}\\ {z = {z_2} + {c_2}{t_2}} \end{array}} \right.,{\mkern 1mu} {\kern 1pt} \left( {{t_2} \in R} \right)$

Từ phương trình của 2 đường thẳng ta suy ra

• Hai điểm bất kì M1(x1, y1, z1) ∈ Δ1 và M2(x2, y2, z2) ∈ Δ2
• Vecto chỉ phương của Δ1: $\overrightarrow {{u_1}} = ({a_1};{b_1};{c_1})$ và Δ2: $\overrightarrow {{u_2}} = ({a_2};{b_1};{c_2})$

Lúc này, công thức tính khoảng cách : d ( Δ1, Δ2 ) = $ \ frac { { \ left | { \ left ( { \ overrightarrow { { u_1 } } \ wedge \ overrightarrow { { u_2 } } } \ right ). \ overrightarrow { { M_1 } { M_2 } } } \ right | } } { { \ left | { \ overrightarrow { { u_1 } } \ wedge \ overrightarrow { { u_2 } } } \ right | } } $

Bài tập có lời giải

Nếu bạn còn vướng mắc về cách về cách tính khoảng cách giữa hai đường thẳng song song hay cách tính khoảng cách giữa 2 đường thẳng chéo nhau thì vui mắt để lại phần phản hồi bên dưới, để toanhoc.org giải đáp giúp bạn .

Source: http://139.180.218.5
Category: tản mạn