Nội dung chính
Phương trình bậc 2 là gì?
Trước khi khám phá công thức nghiệm của phương trình bậc 2, tất cả chúng ta cần hiểu phương trình bậc 2 là gì, có dạng thế nào. Phương trình bậc hai hay còn được gọi là phương trình bậc hai 1 ẩn. Đây là phương trình gồm 1 ẩn số, được tổng quát dưới dạng :
ax2 + bx + c = 0 ( a ≠ 0 )
Trong đó: a, b, c là các số thực được cho trước, x là ẩn số phải đi tìm và a phải là một số khác 0. Bởi nếu a = 0 thì phương trình trên sẽ trở về phương trình bậc 1 có một ẩn số.
Với dạng phương trình này sẽ có nhiều dạng bài tập khác nhau. Tuy nhiên, nhìn chung, những dạng bài tập đều quy về việc tìm nghiệm của phương trình cho trước. Tập nghiệm hoàn toàn có thể gồm 1 hoặc nhiều nghiệm, miễn sao thỏa mãn nhu cầu phương trình .

Công thức nghiệm của phương trình bậc 2
Sau khi đã tìm hiểu và khám phá về phương trình bậc 2, chắc rằng bạn đang vướng mắc công thức nghiệm của phương trình bậc 2 thế nào. Công thức giải phương trình bậc 2 dạng ax2 + bx + c = 0 ( a ≠ 0 ) có Δ = b2 – 4 ac sẽ có 3 trường hợp :
- Δ = 0 : khi đó phương trình sẽ có nghiệm kép hay còn gọi là 2 nghiệm .
- Δ > 0 thì có 2 nghiệm khác nhau là x1 và x2, được tính theo công thức (−b+ / – √Δ ) /2a.
- Trường hợp Δ < 0 thì phương trình bậc 2 kể trên vô nghiệm, tức là phương trình không có số nào thỏa mãn nhu cầu để 2 vế bằng nhau .
Trong trường hợp 2 số thực a, c trái dấu thì phương trình sẽ luôn có 2 nghiệm phân biệt nhau, tức là Δ > 0 .

Định lý Viet trong phương trình bậc 2
Nhắc tới phương trình bậc 2 và công thức giải phương trình bậc 2, tất cả chúng ta không hề không nhắc tới định lý Viet. Đây là một định lý quan trọng, tương quan tới nhiều dạng bài tập của phương trình bậc 2 .
Như đã trình làng ở trên, phương trình bậc 2 có dạng : ax2 + bx + c = 0 ( a ≠ 0 ) sẽ có tối đa 2 nghiệm, gọi là x1 và x2. Khi đó, x1 và x2 sẽ thỏa mãn nhu cầu đồng thời cả 2 điều kiện kèm theo, đó là :
- x1+ x2= – b / a
- x1
x
Xem thêm: Cuộc sống vốn luôn chứa đựng những muộn phiền, cũng may còn có bầu trời luôn cho ta niềm tin!
2= c / a
Khi làm bài tập về phương trình bậc 2, bạn hoàn toàn có thể vận dụng định lý viet bằng cách biến hóa biểu thức để Open x1 + x2 và x1x2 .
Bạn cũng hoàn toàn có thể vận dụng định lý Viet hòn đảo với 2 số x1 và x2 thỏa mãn nhu cầu 2 điều kiện kèm theo :
- x1+ x2= S
- x1x2= P
Trong đó : cả x1 và x2 đều là nghiệm của phương trình x2 – Sx + P = 0 .
Nhắc tới định lý Viet, tất cả chúng ta không hề bỏ lỡ ứng dụng của định lý này. Với phương trình bậc 2, bạn hoàn toàn có thể thuận tiện tính được nghiệm của phương trình mà không cần vận dụng công thức tính nghiệm với 1 số ít trường hợp đặc biệt quan trọng :
- Trường hợp 1 : a + b + c = 0 thì phương trình có 2 nghiệm là x1 = 1 và x2 = c / a .
- Trường hợp 2 : a-b+c = 0 thì phương trình có 2 nghiệm là x1 = – 1 và x2 = – c / a. ( Đây là trường hợp ngược lại của trường hợp 1, bạn cần nhìn kỹ dấu để tránh nhầm lẫn ) .

Dạng bài tập ứng dụng công thức nghiệm của phương trình bậc 2
Sau khi tìm hiểu và khám phá công thức nghiệm của phương trình bậc 2, bạn cần chú ý quan tâm tới những dạng bài tập. Mỗi dạng bài tập sẽ có một chiêu thức giải khác nhau. Áp dụng đúng giải pháp sẽ giúp bạn tiết kiệm chi phí thời hạn và giải bài tập đúng mực hơn .
Cụ thể, lúc bấy giờ phương trình bậc 2 có những dạng bài tập đa phần như :
Dạng 1: phương trình bậc 2 một ẩn không có tham số
Để giải dạng bài tập này, bạn cần vận dụng công thức Δ và Δ ’ rồi vận dụng những công thức tính phương trình bậc 2 đã được ra mắt ở trên. Qua đó tìm được nghiệm của phương trình .
Ví dụ : ta có phương trình : x2-3x+2 = 0. Áp dụng công thức tính Δ, ta sẽ có Δ = 1. Vậy 2 nghiệm của phương trình sẽ lần lượt là :
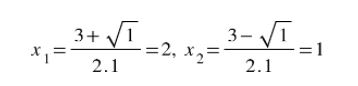
Dạng 2: phương trình bậc 2 một ẩn có tham số
Bên cạnh dạng không chứa tham số, phương trình bậc 2 một ẩn có tham số cũng là một dạng bài tập quan trọng. Để giải dạng bài tập này, bạn cũng cần sử dụng công thức tính Δ. Từ đó, dựa vào 3 trường hợp của Δ đã được lý giải ở trên, bạn hoàn toàn có thể xác lập được phương trình có nghiệm kép, có 2 nghiệm phân biệt hay vô nghiệm. Từ đó vận dụng công thức để tính được những giá trị nghiệm đơn cử .
Trên đây là công thức nghiệm của phương trình bậc 2 và cách giải một số ít dạng bài tập của phương trình bậc 2. Hãy ghi nhớ những công thức, dạng bài tập để hoàn toàn có thể vận dụng khi gặp dạng bài tập này nhé .
Xem thêm:
Source: http://139.180.218.5
Category: tản mạn