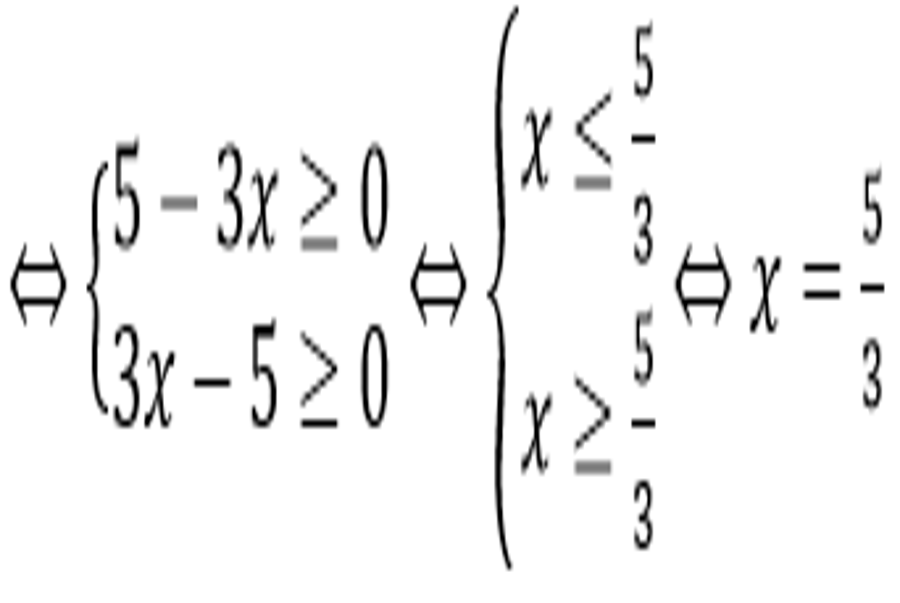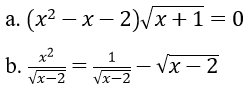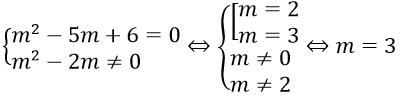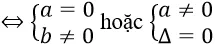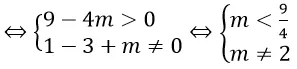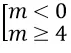Các dạng bài tập chương Phương trình, Hệ phương trình cực hay, có đáp án

Trang trước Trang sauNội dung chính

• Các dạng bài tập chương Phương trình, Hệ phương trình cực hay, có đáp án
• Cách giải phương trình bằng phương pháp biến đổi tương đương
• Cách giải và biện luận phương trình bậc nhất
• Phương pháp giải và biện luận phương trình bậc hai

Phần dưới là các dạng bài tập Toán 10 Đại số Chương 3: Phương trình, Hệ phương trình. Bạn vào tên bài hoặc Xem chi tiết để theo dõi các dạng bài Toán lớp 10 Đại số tương ứng.

Cách giải phương trình bằng phương pháp biến đổi tương đương

– Phương trình tương đương: Hai phương trình f1(x) = g1(x) và f2(x) = g2(x) được gọi là tương đương nếu chúng có cùng tập nghiệm

– Kí hiệu là f1 ( x ) = g1 ( x ) f2 ( x ) = g2 ( x )- Phép đổi khác không làm đổi khác tập nghiệm của phương trình gọi là phép biến hóa tương tự .- Phương trình hệ quả : f2 ( x ) = g2 ( x ) gọi là phương trình hệ quả của phương trình f1 ( x ) = g1 ( x ) nếu tập nghiệm của nó chứa tập nghiệm của phương trình f1 ( x ) = g1 ( x )- Kí hiệu là f1 ( x ) = g1 ( x ) f2 ( x ) = g2 ( x )- Để giải phương trình ta triển khai những phép biến hóa để đưa về phương trình tương tự với phương trình đã cho đơn thuần hơn trong việc giải nó. Một số phép đổi khác thường sử dụng :+ Cộng ( trừ ) cả hai vế của phương trình mà không làm biến hóa điều kiện kèm theo xác lập của phương trình ta thu được phương trình tương tự phương trình đã cho .+ Nhân ( chia ) vào hai vế với một biểu thức khác không và không làm biến hóa điều kiện kèm theo xác lập của phương trình ta thu được phương trình tương tự với phương trình đã cho .+ Bình phương hai vế của phương trình ta thu được phương trình hệ quả của phương trình đã cho .Bình phương hai vế của phương trình ( hai vế luôn cùng dấu ) ta thu được phương trình tương tự với phương trình đã cho .

Bài 1: Giải phương trình

Hướng dẫn:

Điều kiện :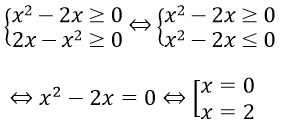Thử lại ta thấy cả x = 0 và x = 2 đều thỏa mãn nhu cầu phương trìnhVậy tập nghiệm của phương trình là S = { 0 ; 2 }

Bài 2: Giải phương trình

Hướng dẫn:

Điều kiện :Ta thấy x = 3 thỏa mãn nhu cầu điều kiện kèm theo ( * )Nếu x 3. thì ( * )Do đó điều kiện kèm theo xác lập của phương trình là x = 3 hoặc x = 5/3Thay x = 3 và x = 5/3 vào phương trình thấy chỉ có x = 3 thỏa mãn nhu cầuVậy phương trình đã cho có nghiệm duy nhất S = { 3 }

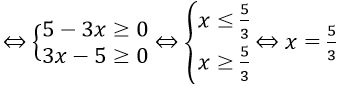
Bài 3: Giải phương trình

Hướng dẫn:

a. Điều kiện : x – 1 .Ta có x = – 1 là một nghiệm .Nếu x > – 1 thì ( x + 1 ) > 0. Do đó phương trình tương tựx2 – x – 2 = 0 x = – 1 hoặc x = 2 .Đối chiếu điều kiện kèm theo ta được nghiệm của phương trình là x = – 1, x = 2 .Vậy phương trình đã cho có hai nghiệm S = { – 1 ; 2 }b. ĐKXĐ : x > 2Với điều kiện kèm theo đó phương trình tương tự với phương trìnhx2 = 1 – ( x – 2 ) x2 + x – 3 = 0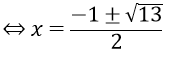Đối chiếu với điều kiện kèm theo ta thấy không có giá trị nào thỏa mãn nhu cầuVậy phương trình vô nghiệm

Cách giải và biện luận phương trình bậc nhất

Cách giải và biện luận phương trình dạng ax + b = 0 được tóm tắt trong bảng sau

Khi a 0 phương trình ax + b = 0 được gọi là phương trình bậc nhất một ẩn

Bài 1: Cho phương trình (m2 – 7m + 6)x + m2 – 1 = 0

a. Giải phương trình khi m = 0b. Biện luận theo m số nghiệm của phương trình

Hướng dẫn:

a. Với m = 0 phương trình trở thành 6 x – 1 = 0 x = 1/6

Phương trình có nghiệm duy nhất x = 1/6

b. Ta có ( mét vuông – 7 m + 6 ) x + mét vuông – 1 = 0 ( m-1 ) ( m-6 ) x + ( m-1 ) ( m + 1 ) = 0Nếu ( m-1 ) ( m-6 ) 0thì phương trình có nghiệm duy nhất x = – ( m + 1 ) / ( m-6 )Nếu m = 1 phương trình trở thành 0 = 0. Khi đó phương trình có vô số nghiệm .Nếu m = 6 thì phương trình trở thành 35 = 0 ( Vô lí ). Khi đó phương trình vô nghiệm .

Bài 2: Tìm tất cả các giá trị thực của tham số m để phương trình (2m – 4)x = m – 2 có nghiệm duy nhất.

Hướng dẫn:

Phương trình đã cho có nghiệm duy nhất khi 2 m – 4 0 m 2

Bài 3: Tìm tất cả các giá trị thực của tham số m để phương trình (m2 – 5m + 6)x = m2 – 2m vô nghiệm.

Hướng dẫn:

Phương trình đã cho vô nghiệm khi

Phương pháp giải và biện luận phương trình bậc hai

Giải và biện luận phương trình bậc hai ax2 + bx + c = 0Bước 1. Biến đổi phương trình về đúng dạng ax2 + bx + c = 0Bước 2. Nếu thông số a chứa tham số, ta xét 2 trường hợp :- Trường hợp 1 : a = 0, ta giải và biện luận ax + b = 0 .- Trường hợp 2 : a 0. Ta lập Δ = b2 – 4 ac. Khi đó :+ Nếu Δ > 0 thì phương trình có 2 nghiệm phân biệt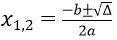+ Nếu Δ = 0 thì phương trình có 1 nghiệm ( kép ) : x = – b / 2 a+ Nếu Δ < 0 thì phương trình vô nghiệm .Bước 3. Kết luận .Lưu ý :- Phương trình ax2 + bx + c = 0 có nghiệm– Phương trình ax2 + bx + c = 0 có nghiệm duy nhất

Bài 1: Phương trình (m1)x2 + 3x  1 = 0. Phương trình có nghiệm khi:

Hướng dẫn:

Với m = 1, phương trình trở thành 3 x – 1 = 0 x = 1/3Do đó m = 1 thỏa mãn nhu cầu .Với m 1, ta có Δ = 9 + 4 ( m-1 ) = 4 m + 5Phương trình có nghiệm khi Δ 0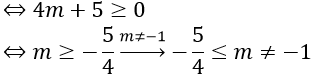Hợp hai trường hợp ta được m – 5/4 là giá trị cần tìm

Bài 2: Phương trình (x2 – 3x + m)(x – 1) = 0 có 3 nghiệm phân biệt khi:

Hướng dẫn:

Phương trình ( x2 – 3 x + m ) ( x – 1 ) = 0Phương trình ( 1 ) có 3 nghiệm phân biệtPhương trình ( 2 ) có hai nghiệm phân biệt khác 1

Bài 3: Có bao nhiêu giá trị nguyên của tham số m thuộc đoạn [-10; 10] để phương trình mx2 – mx + 1 = 0 có nghiệm.

Hướng dẫn:

Nếu m = 0 thì phương trình trở thành 1 = 0 : vô nghiệm .Khi m 0, phương trình đã cho có nghiệm khi và chỉ khiΔ = mét vuông – 4 m 0Kết hợp điều kiện kèm theo m 0, ta được

Vì  Z, m  [-10;10] m  {-10; -9; -8;…; -1}  {4; 5; 6;…; 10}

Vậy có tổng thể 17 giá trị nguyên m thỏa mãn nhu cầu bài toán

Giới thiệu kênh Youtube Tôi

Trang trước Trang sau