1. Định nghĩa về chu vi là gì?

Chu vi là độ dài đo được của một đường khép kín bao quanh một mặt phẳng 2 chiều, hoặc ta hoàn toàn có thể hiểu chu vi là độ dài đường bao quang diện tích quy hoạnh của một hình. Theo đó, ta có chu vi hình vuông vắn, chu vi hình chữ nhật, chu vi hình tròn trụ … với các cách tính tương ứng khác nhau.

2. Chu vi và cách tính chu vi của các hình trong toán học

Trong toán học, có rất nhiều loại hình khác nhau như hình tròn, hình chữ nhật, hình vuông, hình tam giác,hình thang… Trong đó, các hình này đều có chu vi của nó và cách tính theo công thức riêng mà học sinh cần phải nắm được. Sau đây là chi tiết về định nghĩa chu vi và cách tính chu vi của các hình trong toán học.

2.1. Chu vi và cách tính chu vi hình tròn

Chu vi hình tròn trụ chính là độ dài của đường biên giới của hình tròn trụ đó. Người ta sẽ tính chu vi hình tròn trụ theo công thức riêng. Cụ thể công thức tính chu vi hình tròn trụ là lấy pi ( lấy bằng 3,14 ) nhân với đường kính của đường tròn đó, hay chính là pi nhân với 2 lần nửa đường kính của đường tròn, vì đường kính bằng nửa đường kính nhân với 2. Theo đó, ta có công thức tính chu vi của hình tròn trụ là :

P = d x pi hoặc P = r x 2 x pi

Trong đó : + P. là kí hiệu của chu vi hình tròn trụ + d là đường kính của hình tròn trụ + r là nửa đường kính của hình tròn trụ. + pi có giá trị sấp sỉ với 3,14. Số pi được định nghĩa là tỷ suất của chu vi hình tròn trụ.

Ví dụ: Tính chu vi của một chiếc bánh xe có đường kinh là 0,75m.

Trả lời : Đây là bài toán đơn thuần, có một phép tính mà các bạn chỉ cần vận dụng công thức ở trên và thay số vào tính phép tính. Bởi đầu bài cho đường kính của hình tròn trụ, biết số pi. Vậy chu vi của bánh xe hình tròn trụ đó là : P = d.pi = 0,75 x 3,14 = 2,355 ( m ) Như vậy, chu vi của hình tròn trụ là 2,355 ( m )

2.2. Chu vi và cách tính chu vi hình chữ nhật

Tương tự như định nghĩa chung về chu vi, chu vi hình chữ nhật là độ dài của đường bao quanh một mặt phẳng hình chữ nhật. Trong khi đó, hình chữ nhật có bốn góc vuông nên cũng là một hình bình hành và hình thang cân nên có toàn bộ các đặc thù của một hình thang cân và hình bình hành. Theo đó, tổng chiều dài cộng chiều rộng nhân đôi chính là chu vi của hình chữ nhật. Ta có công thức tính chu vi hình chữ nhật như sau :

P = (A + B) x 2

Trong đó : + A là kí hiệu của chiều dài hình chữ nhật + B là kí hiệu của chiều rộng hình chữ nhật + P. là chu vi hình chữ nhật

Ví dụ: Tính chu vi chiếc bánh hình chữ nhật khi biết chiều dài các cạnh lần lượt là 6cm và 3cm.

Trả lời : Đầu bài cho biết độ dài của chiều rộng và chiều dài của chiếc bánh hình chữ nhật. Vì vậy, ta chỉ cần vận dụng công thức tính chu vi ở trên và thay số, tính phép tính là ra hiệu quả. Ta có công thức tính chu vi hình chữ nhật : P = ( a + b ) x 2 = ( 6 + 3 ) x 2 = 9 x 2 = 18 ( cm ) Như vậy chu vi của chiếc bánh hình chữ nhật là 18 cm.

2.3. Chu vi và cách tính chu vi hình vuông

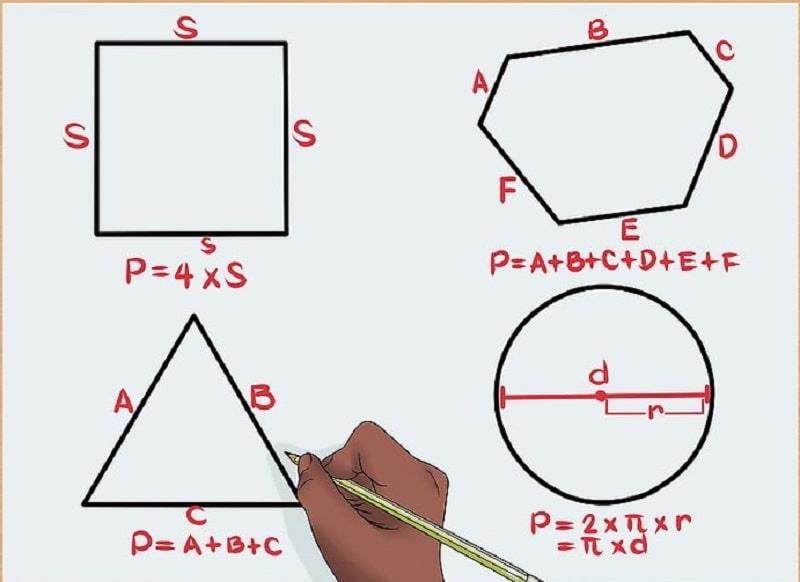
Chu vi hình huông là độ dài của đường bao quanh một hình hai chiều hay hình vuông vắn. Hình vuông là hình có 4 cạnh bằng nhau và 4 góc vuông 90 độ. Do đó, cách tính chu vi hình vuông vắn khá đơn thuần, theo công thức sau :

P = a x 4

Trong đó : + a là cạnh bấy kì của hình vuông vắn + P. là chu vi của hình vuông vắn. Tóm lại, chu vi của hình vuông vắn chính là tổng độ dài của 4 cạnh góc vuông đó hay bằng độ dài một cạnh nhân với 4.

Ví dụ: Cho độ dài cạnh góc vuông của cái bảng bằng 6 cm. Tính chu vi hình vuông của cái bảng đó.

Trả lời : Đề bài cho biết một cạnh góc vuông nên ta hoàn toàn có thể vận dụng công thức tính hình vuông vắn và thay số tính phép tính. Ta có công thức P = a x 4 = 6 x 4 = 24 ( cm ) Vậy chu vi của chiếc bảng đó bằng 24 cm.

2.4. Chu vi và cách tính chu vi hình tam giác

Hình tam giác là một hình gồm có 3 cạnh như tên gọi của nó. Ta có tam giác thường, tam giác vuông với 1 góc vuông 90 độ và tam giác đều có 3 cạnh bằng nhau hay tam giác cân, tam giác tù, tam giác nhọn và tam giác vuông cân. Dù là các hình tam giác khác nhau nhưng chu vi của hình tam giác vẫn là tổng của 3 cạnh cộng lại. Dựa vào đặc thù của từng hình, bạn sẽ có công thức tính có một chút ít độc lạ.

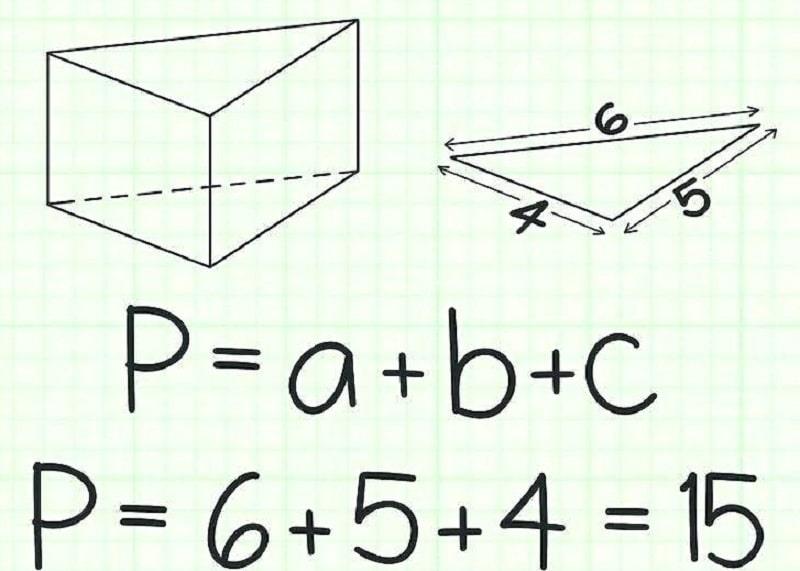
a. Cách tính chu vi của hình tam giác thường

Tam giác thường là hình tam giác có các cạnh và các góc khác nhau. Các hình tam giác thường có các cạnh khác nhau có chung cách tính chu vi, đó là tổng của 3 cạnh cộng lại. Chu vi hình tam giác thường bằng tổng ba cạnh cộng lại. Công thức tính chu vi hình tam giác thường là P = a + b + c. Trong đó : a, b, c là lần lượt 3 cạnh của hình tam giác.

Ví dụ: Tính chu vi hình tam giác thường ABC khi biết chiều dài các cạnh lần lượt là 2,3,4 cm.

Trả lời : Vì đề bài cho độ dài của 3 cạnh hình tam giác nên ta vận dụng công thức P = a + b + c = 2 + 3 + 4 = 9 ( cm ). Vậy chu vi của hình tam giác đã cho là 9 cm.

b. Tính chu vi của hình tam giác vuông

Hình có 3 cạnh và có góc vuông là một tam giác vuông. Cách tính chu vi của hình tam giác vuông dựa theo công thức sau :

P = a + b + h

Trong đó : + A và B là hai cạnh của hình tam giác vuông đó. + h là chiều cao của hình tam giác, nối từ đỉnh xuống đáy hình.

c. Công thức tính chu vi của hình tam giác cân

Chu vi hình tam giác cân tính theo công thức: P = a + b + c

Vì là hình vuông vắn cân nên sẽ tính bằng 2 a + c hoặc 2 b + c.

d. Công thức tính chu vi của hình tam giác đều

Tam giác đều là hình có 3 cạnh bằng nhau nên công thức tính chu vi sẽ là P = a x 3 = b x 3 = c x 3.

Như vậy, chu vi của hình tam giác nói Kết luận là tổng của 3 cạnh của hình cộng lại. Mặc dù mỗi hình tam giác có những đặc thù, đặc thù riêng nên tổng chu vi sẽ có những cách tính tổng tương ứng.

2.5. Tính chu vi hình bình hành

Tứ giác có 2 cặp cạnh đối song song và bằng nhau chính là hình bình hành. Đó là một dạng đặc biệt quan trọng của hình thang với các góc đối bằng nhau. Theo đó, chu vi hình bình hành bằng tổng một cặp cạnh kề nhau bất kể nhân với 2. Hay chi vi hình bình hành chính là tổng độ dài 4 cạnh của hình. Ta có công thức tính chu vi như sau : C = 2 ( a + b ). Trong đó : + a và b : là 2 cạnh kế nhau bất kể của hình bình hành. + C là kí hiệu chu vi của hình bình hành.

Ví dụ: Tính chu vi của một miếng bánh hình bình hành khi biết độ dài của các cạnh a = 4cm, b = 8cm.

Trả lời : Đề bài đã cho 2 cạnh kề nhau của miếng bánh hình bình hành nên ta vận dụng công thức tính chu vi hình bình hành là C = 2 ( a + b ) = 2 ( 4 x 8 ) = 2 x 12 = 24 ( cm ) Vậy chu vi của miếng bánh hình bình hành là 24 cm.

2.6. Chu vi và cách tính chu vi hình thang

Hình thang là một tứ giác lồi có 2 cạnh đáy song song với nhau và các cạnh bên còn lại. Trong đó, có hình thang vuông với một góc vuông 90 độ và hình thang cân có 2 góc kề một đáy bằng nhau. Theo đó, tổng độ dài của hai cạnh đáy và hai cạnh bên chính là chu vi của hình thang. Nghĩa là chu vi hình thang sẽ bằng tổng của tổng thể các cạnh cộng lại. Công thức tính chu vi hình thang như sau :

P = a + b + c + d

Trong đó : + P. là kí hiệu của chu vi hình thang + a, b, c, d là các cạnh của hình thoi.

Ví dụ: Tính chu vi hình thang khi biết độ dài của đáy lớn là 10 cm, đáy nhỏ là 8cm và độ dài 2 cạnh bên lần lượt là 6cm và 9cm.

Trả lời : Đề bài cho biết độ dài của 2 cạnh đáy và 2 cạnh bên nên vận dụng công thức tính chu vi hình thang ta có : P = a + b + c + d = 10 + 8 + 6 + 9 = 33 ( cm ) Vậy chu vi của hình thang đó là 33 cm.

Lưu ý: Tính chu vi hình thang bình thương hay hình thang cân, hình thang vuông đều giống nhau, bằng tổng của 2 cạnh đáy và 2 cạnh bên cộng lại.

Tóm lại, chu vi của các hình học trong toán sẽ là tổng của các cạnh cộng lại với nhau tương ứng. Nếu là hình tam giác sẽ là tổng của 3 cạnh cộng lại, nếu là hình chữ nhật, hình vuông vắn sẽ là tổng của 4 cạnh cộng lại … Tuy nhiên, mỗi hình sẽ có những đặc thù khác nhau mà chu vi cũng theo đó mà có các công thức tương ứng mà bạn cần ghi nhớ. Nhưng nhìn chung, bạn chỉ cần hiểu rằng chu vi chính là tổng của độ dài của đường xung quanh hình mặt phẳng đó để thuận tiện nắm kỹ năng và kiến thức hơn. Thêm vào đó, mỗi hình sẽ có các đặc thù đặc biệt quan trọng của nó phân biệt với các hình khác mà bạn cần nắm được sẽ dễ học chu vi của hình hơn cả, dễ tính chu vi hơn. Tóm lại, chu vi là gì và cách tính chu vi của các loại hình học trong toán ở trên là những kỹ năng và kiến thức quan trọng và được vận dụng nhiều trong chương trình học mà các bạn học viên cần ghi nhớ.

>> Xem thêm:

• Công thức tính chu vi, diện tích hình tròn
• Công thức tính chu vi, diện tích tam giác
• Công thức tính chu vi, diện tích hình thang cần nhớ

Source: http://139.180.218.5
Category: tản mạn