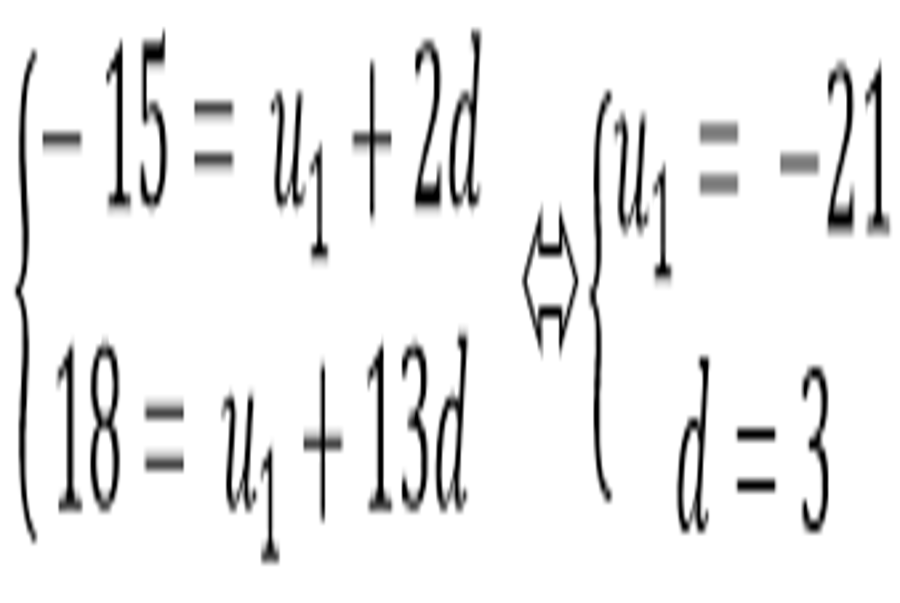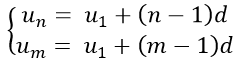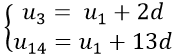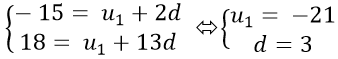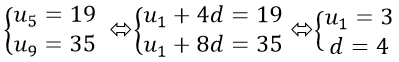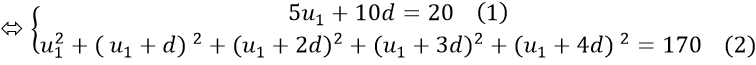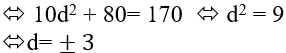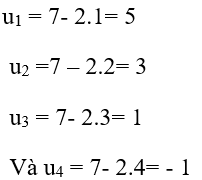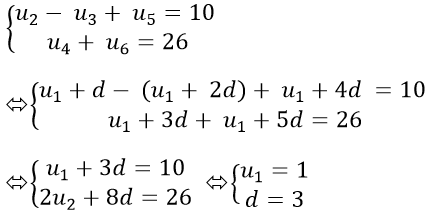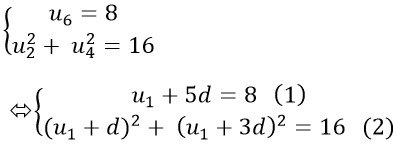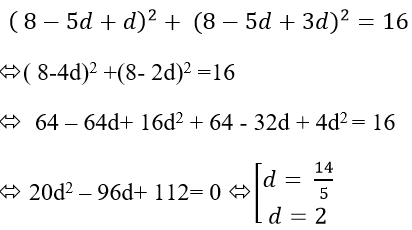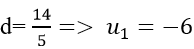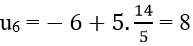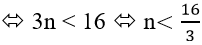Cách tìm số hạng đầu tiên, công sai, số hạng thứ k của cấp số cộng cực hay
A. Phương pháp giải
+ Dãy số ( un ) là cấp số cộng khi và chỉ khi un + 1 − un = d không phụ thuộc vào vào n và d là công sai .
+ Cho cấp số cộng có số hạng đầu là u1; công sai d. Khi đó; số hạng thứ n của cấp số cộng là: un = u1 + (n−1)d
+ Nếu biết số hạng thứ n và thứ m của dãy ta suy ra :
Giải hệ phương trình trên ta được u1 và công sai d .
B. Ví dụ minh họa
Ví dụ 1: Cho cấp số cộng (un) có u1 = 0,4 và công sai d = 1. Số hạng thứ 10 của cấp số cộng này là:
A. 1,6 B. 1,4 C. 10,4 D. 9,4
Hướng dẫn giải:
Số hạng tổng quát của cấp số cộng ( un ) là : un = u1 + ( n − 1 ) d
=> số hạng thứ 10 của cấp số cộng là :
u10 = 0,4 + ( 10 − 1 ). 1 = 9,4
Chọn D .
Ví dụ 2: Cho cấp số cộng (un) có u3 = −15 và u14 = 18. Tìm u1, d của cấp số cộng?
A. u1 = − 21 ; d = 3 B. u1 = − 20 ; d = 2
C. u1 = − 21 ; d = − 3 D. u1 = − 20 ; d = − 2
Hướng dẫn giải:
Ta có: 
Từ giả thiết suy ra: 
Chọn A .
Ví dụ 3: Cho cấp số cộng ( un) thỏa mãn :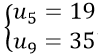 
. Tìm số hạng thứ 10 của cấp số.
A. 39 B. 27
C. 36 D. 42
Hướng dẫn giải:
Theo giả thiết ta có :
=> Số hạng thứ 10 của cấp số cộng là :
u10 = u1 + 9 d = 3 + 9. 4 = 39
Chọn A .
Ví dụ 4: Cho cấp số cộng (un) thỏa mãn điều kiện: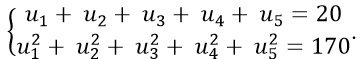 
. Tìm công sai của cấp số cộng đã cho.
A.d = ± 1 B.d = ± 2 C. d = ± 3 D. d = ± 4
Hướng dẫn giải:
Theo đề bài ta có :
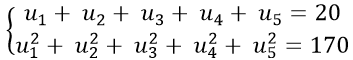
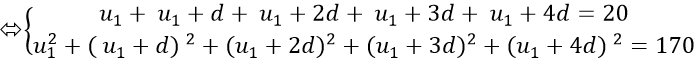
Từ ( 1 ) suy ra : u1 + 2 d = 4 ⇔ u1 = 4 − 2 d thế vào ( 2 ) ta được :
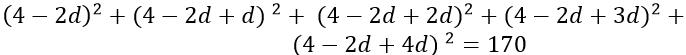
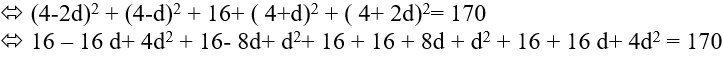
* Với d = 3 => u1 = 4 − 6 = − 2
* Với d = − 3 => u1 = 4 + 6 = 10
Chọn C .
Ví dụ 5: Cho dãy số (un) với un = 7 − 2n. Khẳng định nào sau đây là sai?
A. 3 số hạng đầu của dãy u1 = 5 ; u2 = 3 và u3 = 1 .
B. Số hạng thứ n + 1 là un + 1 = 8 − 2 n .
C. Là cấp số cộng có d = − 2 .
D. Số hạng thứ 4 : u4 = − 1 .
Hướng dẫn giải:
* Ta có :
=> đáp án A, D đúng .
* Số hạng thứ n + 1 là : un + 1 = 7 − 2 ( n + 1 ) = 5 − 2 n
=> B sai .
* Xét hiệu : un + 1 − un = ( 5 − 2 n ) − ( 7 − 2 n ) = − 2
=> ( un ) là cấp số cộng với công sai d = − 2 .
=> C đúng .
Ví dụ 6: Cho một cấp số cộng có u1 = −1 và u5 = 11. Tìm công sai của cấp số cộng ?
A. d = 3 B. d = 5 C. d = 4 D. d = 2
Hướng dẫn giải:
Ta có : u5 = u1 + ( 5 − 1 ) d
=> 11 = − 1 + 4 d ⇔ d = 3
Chọn A .
Ví dụ 7: Cho một cấp số cộng có u1 = 10; u7 = −8. Tìm d?
A. d = − 2 B. d = − 3 C. d = 2 D.d = 3
Hướng dẫn giải:
Ta có : u7 = u1 + ( 7 − 1 ) d
=> − 8 = 10 + 6 d
⇔ − 18 = 6 d nên d = − 3
Chọn B .
Ví dụ 8: Cho cấp số cộng (un) thỏa mãn :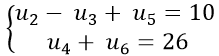 
. Hỏi 301 là số hạng thứ bao nhiêu của cấp số cộng.
A. 99 B. 100
C. 101 D. 103
Hướng dẫn giải:
Theo giả thiết ta có :
Ta có : 301 = 1 + ( n − 1 ). 3 ⇔ 300 = 3 ( n-1 )
⇔ n − 1 = 100 ⇔ n = 101
Vậy 301 là số hạng thứ 101 của cấp số cộng .
Chọn C .
Ví dụ 9: Cho cấp số cộng (un) thỏa mãn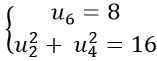 
. Tìm số hạng thứ 6 của cấp số cộng ?
A. 8 B. 10
C. 6 D. 12
Hướng dẫn giải:
Theo giả thiết ta có :
Từ (1) suy ra : u1 = 8 − 5d thay vào (2) ta được : 
Với 
Số hạng thứ 6 là: 
Với d = 2 => u1 = − 2
Số hạng thứ 6 : u6 = − 2 + 5. 2 = 8
Chọn A .
Ví dụ 10: Cho cấp số cộng (un) có u1 = −2 và công sai d = 3. Hỏi có bao nhiêu số hạng của cấp số thỏa mãn un < 11.
A. 3 B. 4 C. 5 D. 6
Hướng dẫn giải:
Cấp số cộng có u1 = − 2 và công sai d = 3 nên số hạng tổng quát của cấp số cộng là :
un = u1 + ( n − 1 ). d = − 2 + 3 ( n − 1 ) = 3 n − 5
Để un < 11 thì 3 n − 5 < 11
Mà n nguyên dương nên n ∈ { 1,2,3,4,5 }
Vậy có 5 số hạng của cấp số cộng thỏa mãn nhu cầu điều kiện kèm theo
Chọn C .
Ví dụ 11: Viết ba số xen giữa các số 2 và 22 để được cấp số cộng có 5 số hạng. Tính tổng của ba số hạng xen giữa đó.
A. 36 B. 28 C. 32 D. 30
Hướng dẫn giải:
Khi viết ba số xen giữa hai số 2 và 22 để được cấp số cộng có 5 số hạng thì :
u1 = 2 và u5 = 22 .
+ Lại có : u5 = u1 + ( 5 − 1 ) d nên 22 = 2 + 4 d
⇔ 20 = 4 d ⇔ d = 5
+ Suy ra : u2 = u1 + d = 2 + 5 = 7
u3 = u1 + 2 d = 2 + 2. 5 = 12
Và u4 = u1 + 3 d = 2 + 3. 5 = 17
=> u2 + u3 + u4 = 7 + 12 + 17 = 36
Chọn A .
C. Bài tập trắc nghiệm
Câu 1: Cho (un) là cấp số cộng thỏa mãn :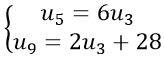 
. Tìm số hạng thứ 20 của cấp số cộng.
A. 67 B. 75
C. 87 D. 91
Câu 2: Tìm ba số hạng liên tiếp của một cấp số cộng biết tổng của chúng bằng −9 và tổng các bình phương của chúng bằng 29.
A. 0 ; − 3 ; − 6 B. − 2 ; − 3 ; − 4
C. − 1 ; − 2 ; − 3 D. − 3 ; − 2 ; − 1
Câu 3: Cho dãy số (un) là cấp số cộng thỏa mãn: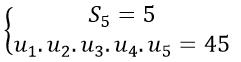 
Tính số hạng thứ 4 của cấp số cộng.
A. 3 hoặc − 1 B. 2 hoặc − 2 .
C. 2 hoặc − 3 D. − 2 hoặc 1 .
Câu 4: Cho 2 cấp số cộng : 5 ;8 ;11 ; …..và 3 ;7 ;11,…. Hỏi trong 100 số hạng đầu tiên của mỗi cấp số ; có bao nhiêu số hạng chung ?
A. 23 B. 24
C. 25 D. Tất cả sai
Câu 5: Cho cấp số cộng (un) có u2 + u3 = 20; u5 + u7 = −29. Tìm u1 ; d?
A. u1 = 20 ; d = 7 B. u1 = 20 ; d = 7
C. u1 = 20,5 ; d = − 7 D. u1 = − 20,5 ; d = 7
Câu 6: Cho cấp số cộng (un) thỏa mãn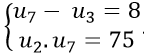 
. Tìm u1 ;d biết u1 > 0
A. u1 = 3 ; d = 1 B. u1 = 3 ; d = 2
C. u1 = 2 ; d = 3 D. u1 = 2 ; d = − 3
Câu 7: Cho cấp số cộng (un) có công sai d > 0 và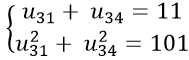 
. Hãy tìm số hạng tổng quát của cấp số cộng đó.
A. un = 3 n − 9 B. un = 3 n − 42
C. un = 3 n − 67 D. un = 3 n − 92
Câu 8: Tam giác ABC có ba góc A, B, C theo thứ tự đó lập thành cấp số cộng và C = 5A. Tính tổng số đo của góc có số đo lớn nhất và góc có số đo nhỏ nhất.
A. 1400 B. 1200
C. 1350 D. 1500
Câu 9: Cho (un) là cấp số cộng thỏa mãn :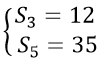 
. Tính tổng của số hạng đầu tiên và công sai d ?
A. 3 B. 4
C. 5 D. 6
Câu 10: Cho (un) là cấp số cộng, u1; u2; u3 là 3 số hạng của cấp số cộng thỏa mãn: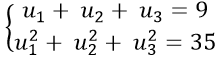 
. Tìm tích 3 số đó?
A. 15 B. 20
C. 21 D. 18
Câu 11: Cho cấp số cộng (un) có u4 = −20; u19 = 55. Tìm u1, d của cấp số cộng?
A. u1 = − 35 ; d = 5 B. u1 = − 35 ; d = − 5
C. u1 = 35 ; d = 5 D. u1 = 35 ; d = − 5
Câu 12: Cho (un) là cấp số cộng thỏa mãn :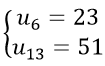 
. Tìm số hạng thứ 2 của cấp số cộng.
A. 6 B. 7
C. 8 D. 9
Source: http://139.180.218.5
Category: tản mạn