Nội dung chính [ẩn đi]
1. Tam giác đều là gì?
Trong hình học, tam giác đều là tam giác có ba cạnh bằng nhau hoặc tương tự bagócbằng nhau và bằng 60 °Tam giác ABC đều có AB = AC = BC .
2. Tính chất
Trong một tam giác đều, mỗi góc bằng 600.
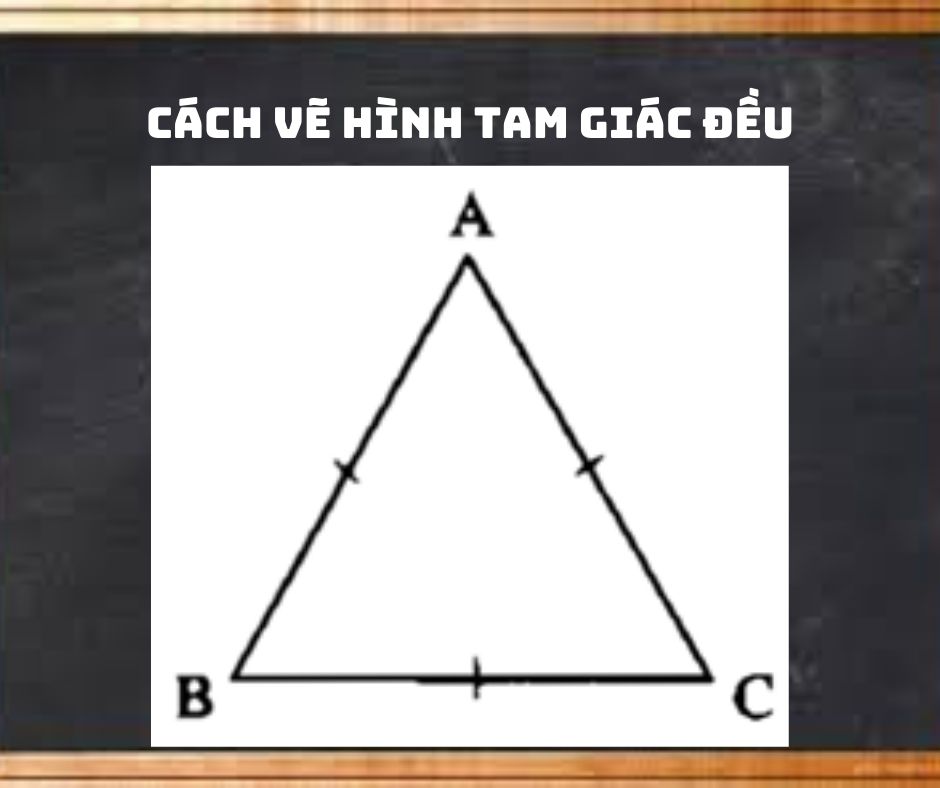
Bạn đang đọc: Cách vẽ hình tam giác đều
Tam giác ABC đều
Nếu một tam giác có ba góc bằng nhau thì tam giác đó là tam giác đều .
NếuA = B = C thì tam giác ABC đều
Nếu một tam giác cân có một góc bằng 600 thì tam giác đó là tam giác đều .
Tam giác ABC cân tại A. Nếu ta cóA = 600 hoặcB = 600 hoặcC = 600 thì tam giác ABC đều .
Trong tam giác đều, đường trung tuyến của tam giác đồng thời là đường cao và đường phân giác của tam giác đó .
Tam giác ABC đều có AD là đường trung tuyến kẻ từ đỉnh A. Khi đó, AD là đường cao và đường phân giác của tam giác ABC .
3. Làm sao để nhận biết đó là tam giác đều?
– Đó là tam giác đều khi tam giác đó có ba cạnh bằng nhau
– Tam giác có ba góc bằng nhau là tam giác đều
– Trong tam giác cân, nếu có một góc bằng 60 ° là tam giác đều
– Một tam giác có hai góc bằng 60 ° là tam giác đều .
4. Cách vẽ hình tam giác đềuvới độ dài cạnh đã cho trước
Tronghình học, tam giác đềulàtam giáccó ba cạnh bằng nhau hoặc tương tự ba góc bằng nhau, và bằng 60 °. Nó là mộtđa giác đềuvới số cạnh bằng 3 .
Để vẽ hình tam giác đều có độ dài cạnh cho trước ta triển khai như sau :
– Bước 1 : Gọi AB là 1 đoạn thẳng ( Giả sử dài 4 cm ). Sau đó, đo khoảng cách của compa bằng với đoạn thẳng AB .
– Bước 2 : Từ đầu mút A của đoạn thẳng, đặt kim compa và xoay một đường tròn ngắn. ( Tương tư với đầu mút B ) .
– Bước 3 : Giao điểm của 2 đường tròn là đỉnh của tam giác đều ( gọi là điểm C ). Ta nối 3 điểm C, A, B lại tạo thành tam giác đều CAB có đỉnh là C .
Vẽ hình tam giác đều
5. Cách vẽ tam giác đều bằng compa
– Bước 1 : Vẽ mộtvòng trònbằng compa có tâm là O. Bán kính OA .
– Bước 2 : Từ A, đặt kim compa sao cho điểm tiếp theo trên đường tròn có khoảng cách bằng với nửa đường kính OA. Tượng tự, ta có các điểm cách đều trên đường tròn lần lượt : M, B, D, C, N .
– Bước 3 : Dựng các đường thẳng đi qua các điểm lại với nhau. Ta được tam giác đều .
6. Chu vi tam giác đều
Trong đó, P. là chu vi tam giác ; a là độ dài ba cạnh của tam giác đó .
7. Diện tích tam giác đều
Vì tam giác ABC đều nên đường cao kẻ từ đỉnh A trùng với đường trung tuyến kẻ đỉnh A của tam giác ABC
Diện tích tam giác ABC là :
8. Công thức tính đường cao trong tam giác đều
Công thức tính đường cao trong tam giác đều :
Trong đó :
+ a : Độ dài các cạnh của tam giác đều .
+ h : Chiều cao của hình tam giác đều .
9. Ứng dụng của tam giác đều trong đời sống
Trong đời sống, tam giác đều ứng dụng vào rất nhiều đồ vật có thể kể đến như:
Xem thêm: Tam giác.
– Đồ gia dụng : Kệ treo tường, bàn, ghế, khung ảnh trang trí, dĩa, …
– Dụng cụ học tập : Thước, quy mô miêu tả hình tam giác đều, …
Video liên quan
Source: http://139.180.218.5
Category: tản mạn