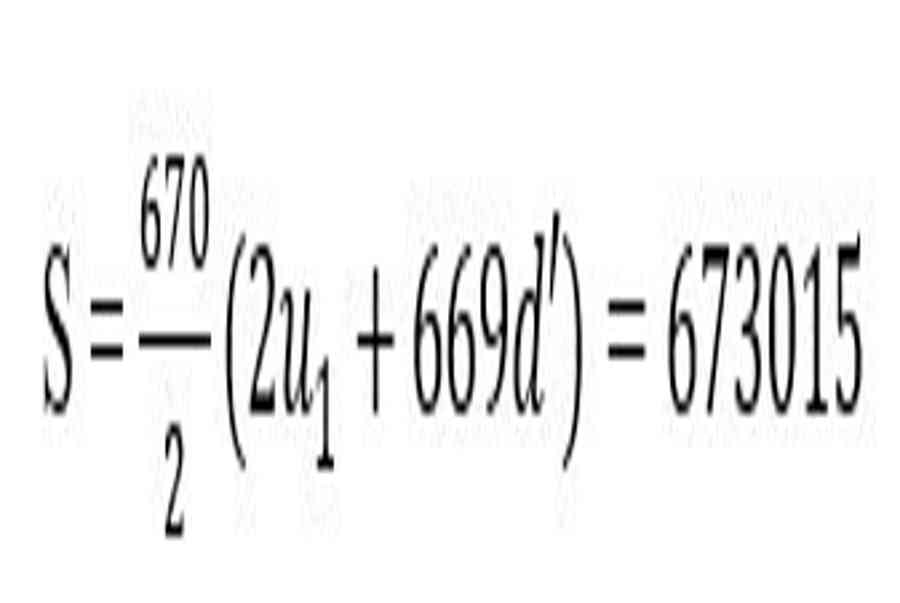Cấp số cộng và cấp số nhân là nội dung toán học quan trọng cần nắm rõ của lớp 11. Trong bài viết này chúng tôi sẽ giúp các bạn ôn tập lại kiến thức về cấp số cộng, cấp số nhân và các dạng bài tập để giúp các bạn có thể nắm rõ nền tảng kiến thức này. là nội dung toán học quan trọng cần nắm rõ của lớp 11. Trong bài viết này chúng tôi sẽ giúp những bạn ôn tập lại kiến thức và kỹ năng về, cấp số nhân và những dạng bài tập để giúp những bạn hoàn toàn có thể nắm rõ nền tảng kỹ năng và kiến thức này .
Nội dung chính
Cấp số cộng là gì?
Khái niệm cấp số cộng
Trong toán học, cấp số cộng là khái niệm được dùng để chỉ một dãy số thỏa mãn nhu cầu điều kiện kèm theo số đứng sau bằng tổng của số đứng trước nó với 1 số ít không đổi. Số không đổi này được gọi là công sai. Dãy số cấp số cộng hoàn toàn có thể là vô hạn hoặc hữu hạn .
Ví dụ : 3, 5, 7, 9, 11, 13, 15, 17, 19, 21, 23 …
Định nghĩa cấp số cộng:
Un là cấp số cộng nếu : un + 1 = un + d
Trong đó :
-
nN
-
d là công sai = un + 1– un
Số hạng tổng quát
Chúng ta hoàn toàn có thể tính được số hạng tổng quát trải qua số hạng đầu và công sai :
-
un= u1+ ( n – 1 ) d, ( trong đó n2 )
Ví dụ :
Cho cấp số cộng ( un ) biết được u1 = – 1 và d = 3. Hãy tìm u20 ?
Ta có :
u20 = u1 + ( 20 – 1 ) d
= u1 + 19 d
= – 1 + 19 × 3
= 65

Tính chất cấp số cộng
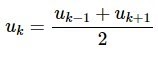
Trong đó : k2 hay uk + 1 + uk-1 = 2 uk
Ví du :
Cho 3 số lần lượt là 9 ; x ; 13 hãy lập một cấp số cộng và tìm X
Ta có ;
x = 9 + 132 = 11
Như vậy ra có x = 11 và cấp số cộng là 9, 11, 13
Tổng n số hạng đầu
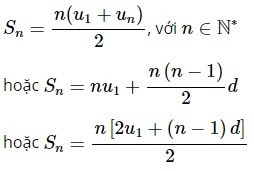
Ví dụ :
Cho cấp số cộng ( un ) thỏa mãn nhu cầu : u1 = – 1, d = 3. hãy triển khai tính S20
Ta có ;
S20 = 20 u1 + 20. ( 20-12 ). d
= 20. ( – 1 ) + 20.192. 3
= 550
Cấp số nhân là gì?
Khái niệm cấp số nhân
Trong toán học cấp số nhân được hiểu là một dãy số thỏa mãn nhu cầu điều kiện kèm theo đó là từ số thứ 2 của dãy số đó đều là tích của số đứng trước nó với 1 số không đổi. Số không đổi này được gọi là công bội của cấp số nhân .
Định nghĩa cấp số nhân
-
unlà cấp số nhân tương tự vớiun + 1=un. q, trong đó n ∈N
- q là công bội và bằng :
![]()
ví dụ : Cho cấp số nhân ( un ). Trong đó u1 = 5 ; q = 3. Thực hiện tính u2 .
Ta có :
u2 = qu1 = 3. 5 = 15

Số hạng tổng quát
Để tính số hạng tổng quát tất cả chúng ta vận dụng công thức sau :
un = u1. qn-1, trong đó n2
Ví dụ : Ta có cấp số nhân ( un ). Trong đó u1 = 5 ; q = 3. Thực hiện tính u5
Ta có : u5 = u1q4 = 5.34 = 405
Tính chất của cấp số nhân
![]()
Ví dụ :
Cho cấp 4 số lần lượt là x ; 5 ; 25 ; y. Theo thứ tự như vậy những bạn hãy thực thi lập một cấp số nhân và triển khai tìm x, y .
Ta có :
52 = x. 25 ⇔ x = 1
252 = 5 y ⇔ y = 125
Như vậy tất cả chúng ta có cấp số nhân là 1, 5, 25, 125
Tổng n số hạng đầu
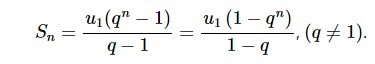
Ví dụ :
Cho cấp số nhân ( un ) với u1 = 5 và q = 3. Thực hiện tính S10 .
Ta có :
S10 = u1 ( 1 – q10 ) 1 – q
= 5. ( 1-310 ) 1-3
= 5 ( 310 – 1 ) 2
Bài tập luyện tập về cấp số cộng cấp số nhân
Bài tập về cấp số cộng
Bài 1: Hãy tìm 4 số hạng liên tiếp của một cấp số cộng biết được rằng:
- Tổng của chúng bằng 20 .
- Tổng những bình phương của chúng bằng 120 .
Lời giải:
Chúng ta giả sử 4 số hạng đó lần lượt là : a-3x, a-x, a + x, a + 3 x. Công sai là d = 2 x. Lúc này ta có :
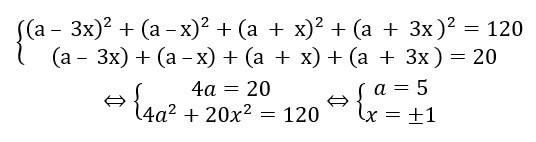
Như vậy bốn số tất cả chúng ta cần tìm lần lượt là 2, 4, 6, 8

Bài tập 2: Cho cấp số cộng sau
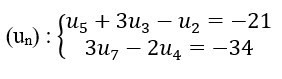
-
Hãy thực hiện tính số hạng thứ 100 của cấp số cộng trên
- Thực hiện tính tổng của 15 số hạng đầu của cấp số cộng
-
Tính S =u4+u5+u5+ … +U30
Lời giải:
Từ giải thiết đề bài đưa ra tất cả chúng ta có :
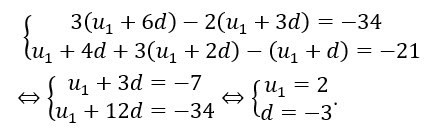
- Thực hiện tìm thứ hạng 100 của cấp số cộng trên ta có :
u100 = u1 + 99 d = – 295
- Tổng của 15 số hạng đầu cấp số cộng :
![]()
-
Tính S =u4+u5+u5+ … +U30
Ta có :
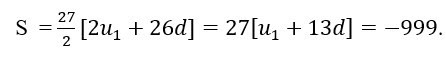
Bài 3: Cho cấp số cộng
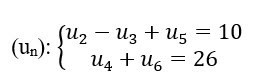
- Thực hiện xác lập công sai, công thức tổng quát cấp số
-
Tính S =u1+u4+u7+ … +u2011
Lời giải:
Ta gọi d là công sai của cấp số cộng đã cho, ta có :
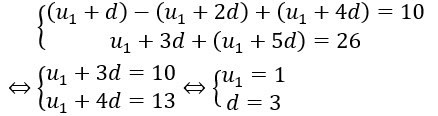
-
Ta có công sai của cấp số cộng trên là d = 3 ; số hạng tổng quát là :un=u1+ ( n-1 ) d = 3 n – 2
-
Từ đề bài ta có những số hạngu1,u4,u7, … ,u2011lập thành một cấp số cộng gồm có 670 số hạng và có công sai d ’ = 3 d. Do đó ta có :
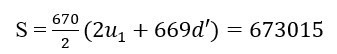
Bài tập về cấp số nhân

Bài tập 1: Cho cấp số nhân (un)có các số hạng khác 0 hãy tìm u1biết:
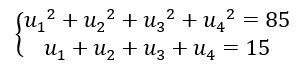
Lời giải:
Ta có :
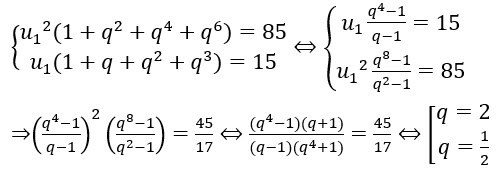
Như vậy ta tìm được u1 = 1, u1 = 8
Bài tập 2: Cho cấp số nhân sau:
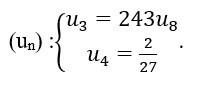
- Hãy tìm 5 số hạng đầu của cấp số nhân trên
- Thực hiện tính tổng của 10 số hạng đầu của cấp số nhân
Lời giải:
Gọi q là bội của cấp số. Theo giải thiết tất cả chúng ta có :
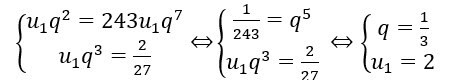
- Năm số hạng đầu của cấp số nhân cần tìm là
u1 = 2, u2 = 23, u3 = 29, u4 = 27, u5 = 281
- Tổng của 10 số hạng tiên phong của cấp số nhân trên :
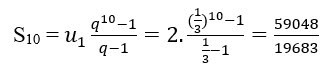
Trên đây là những san sẻ của chúng tôi về cấp số cộng cấp số nhân với những bạn. Hy vọng trải qua bài viết những bạn đã biết được cấp số cộng là gì ? Cấp số nhân là gì ? Cũng như cách giải những bài toán cấp số cộng và cấp số nhân .
Xem thêm:
 Tôi là Nguyễn Tiến Thành – Tôi đã có nhiều năm kinh nghiệm tay nghề review nhìn nhận những loại thiết bị vệ sinh công nghiệp và những mẹo làm sạch. Hy vọng những san sẻ của tôi sẽ đem lại cho những bạn những thông tin có ích hơn .
Tôi là Nguyễn Tiến Thành – Tôi đã có nhiều năm kinh nghiệm tay nghề review nhìn nhận những loại thiết bị vệ sinh công nghiệp và những mẹo làm sạch. Hy vọng những san sẻ của tôi sẽ đem lại cho những bạn những thông tin có ích hơn .
Source: http://139.180.218.5
Category: tản mạn