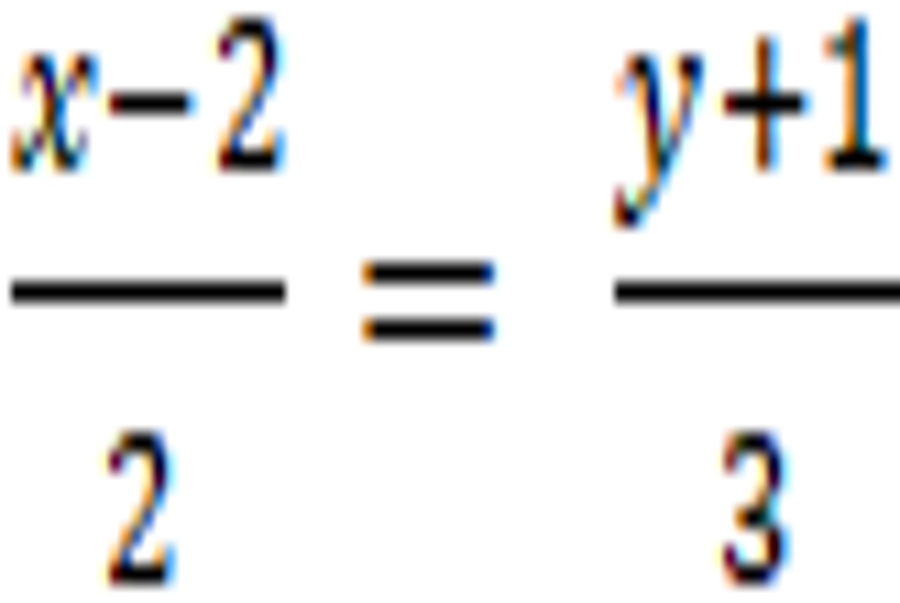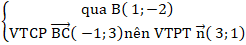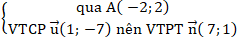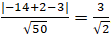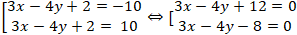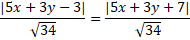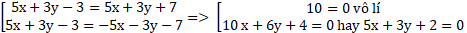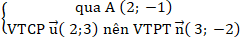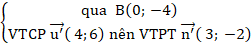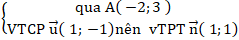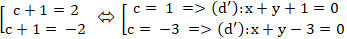Bạn đang đọc: Tìm khoảng cách giữa hai đường thẳng song song
B. Ví dụ minh họa
-
Ví dụ 1: Cho tam giác ABC có B( 1; -2) và C( 0; 1). Điểm A thuộc đường thẳng
d: 3x+ y= 0 .Tính diện tích tam giác ABC.A. 1 B. 3 C. 0,5 D. 2
Lời giải
+ Phương trình đường thẳng BC :
⇒ Phương trình BC : 3 ( x – 1 ) + 1 ( y + 2 ) = 0 hay 3 x + y – 1 = 0 .
+ ta có; BC =
= √10
+ Xét vị trí tương đối giữa đường thẳng d và BC :
Ta có:
⇒ d // BC.
Mà điểm A thuộc d nên d ( A ; BC ) = d ( d ; BC ). ( 1 )
+ Ta tính khoảng cách hai đường thẳng d và BC .
Lấy điểm O ( 0 ; 0 ) thuộc d .⇒ d(d; BC) = d(O;BC) =
=
( 2)
Từ ( 1 ) và ( 2 ) suy ra d ( A ; BC ) = .
+ Diện tích tam giác ABC là S =
d( A,BC).BC = . .√10 = 0, 5
Chọn C.
Ví dụ 2. Tính khoảng cách giữa hai đường thẳng d: 7x + y – 3 = 0 và ∆: 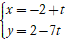
A. 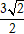
Lời giải
+ Ta đưa đường thẳng ∆ về dạng tổng quát :
∆:
⇒ Phương trình ∆ : 7 ( x + 2 ) + 1 ( y – 2 ) = 0 hay 7 x + y + 12 = 0
Ta có: 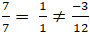
⇒ d(d;Δ) = d(A;d) =
Chọn A.
Ví dụ 3. Tập hợp các điểm cách đường thẳng ∆: 3x – 4y + 2 = 0 một khoảng bằng 2 là hai đường thẳng có phương trình nào sau đây?
A. 3x – 4y + 8 = 0 hoặc 3x – 4y + 12 = 0. B. 3x – 4y – 8 = 0 hoặc 3x – 4y + 12 = 0.
C. 3x – 4y – 8 = 0 hoặc 3x – 4y – 12 = 0. D. 3x – 4y + 8 = 0 hoặc 3x – 4y – 12 = 0.
Lời giải
Gọi điểm M (x ; y) là điểm cách đường thẳng ∆ một khoảng bằng 2. Suy ra :
d(M(x; y); Δ) = 2 ⇔ 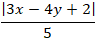
|3x – 4y + 2| = 10 ⇒
Vậy tập hợp các điểm cách ∆ một khoảng bằng 2 là hai đường thẳng :
3 x – 4 y + 12 = 0 và 3 x – 4 y – 8 = 0
Chọn B.
Ví dụ 4. Trong mặt phẳng với hệ tọa độ Oxy, cho hai đường thẳng d1: 5x + 3y – 3 = 0 và d2: 5x + 3y + 7 = 0 song song nhau. Đường thẳng d vừa song song và cách đều với d1; d2 là:
A. 5x + 3y – 2 = 0 B. 5x + 3y + 4 = 0 C. 5x + 3y + 2 = 0 D. 5x + 3y – 4 = 0
Lời giải
Lấy điểm M ( x ; y ) thuộc đường thẳng d. Suy ra :
d(M(x; y); d1)=d(M(x; y); d2) ⇔
⇔
Đường thẳng d : 5 x + 3 y + 2 song song với hai đường thẳng d1 và d2 .
Vậy đường thẳng d thỏa mãn nhu cầu là : 5 x + 3 y + 2 = 0
Chọn C.
Ví dụ 5: Cho đường thẳng d: 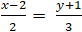
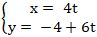
A. 1 B. 0. C. 2 D. 3
Lời giải
+ Đường thẳng d:
⇒ Phương trình d : 3 ( x – 2 ) – 2 ( y + 1 ) = 0 hay 3 x – 2 y – 8 = 0
+ Đường thẳng ∆:
⇒ Phương trình ∆ : 3 ( x – 0 ) – 2 ( y + 4 ) = 0 hay 3 x – 2 y – 8 = 0
⇒ hai đường thẳng này trùng nhau nên khoảng cách hai đường thẳng này là 0 .
Chọn B.
Ví dụ 6: Cho hai đường thẳng d: x + y – 2 = 0 và đường thẳng ∆: 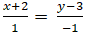
A. x + y – 1 = 0 B. x + y + 1= 0 C. x + y – 3 = 0 D. Cả B và C đúng.
Lời giải
+ Do đường thẳng d ’ / / d nên đường thẳng d có dạng ( d ’ ) : x + y + c = 0 ( c ≠ – 2 )
+ Đường thẳng ∆:
⇒ Phương trình ∆ : 1 ( x + 2 ) + 1 ( y – 3 ) = 0 hay x + y – 1 = 0 .
+ Lấy điểm M ( 1 ; 0 ) thuộc ∆ .
Để khoảng cách hai đường thẳng d ’ và ∆ bằng 2 khi và chỉ khi :
d ( d ’ ; ∆ ) = d ( M ; d ’ ) = 2
⇔ 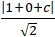
⇔
Vậy có hai đường thẳng thỏa mãn nhu cầu là : x + y + 1 = 0 và x + y – 3 = 0
Chọn D.
Source: http://139.180.218.5
Category: tản mạn