Hình trụ là một mô hình cơ bản, được sử dụng liên tục trong những bài toán hình học từ dễ đến khó. Trong đó, công thức tính thể tích hình tròn trụ là rất quan trọng, nó giúp tính đúng mực khoảng chừng khoảng trống nhất định mà hình tròn trụ chèn lên. Cùng tìm hiểu thêm về công thức tính thể tích hình tròn trụ và những bài toán mẫu hướng dẫn đơn cử về cách tính thể tích của những hình tròn trụ nhé !
Tính thể tích hình lăng trụ (Nguồn: Internet)
Bạn đang đọc: Tổng hợp các Các công thức tính thể tích hình trụ
Khái niệm hình trụ, thể tích của hình trụ
Có rất nhiều loại hình trụ trong khoảng trống, 1 số ít hình tròn trụ cơ bản thường gặp trong những bài toán như hình tròn trụ tròn, hình lăng trụ đứng, hình tròn trụ tam giác. Hình trụ là một hình khối, được tạo thành bởi hai mặt đáy song song và bao quanh bởi vỏ mặt bên. Cụ thể :
- Hình trụ tròn là hình được tạo bởi hai mặt đáy là hai hình tròn trụ song song với nhau .
- Hình trụ tam giác được tạo bởi hai mặt đáy là hai hình tam giác song song, bao quanh là những hình bình hành .
- Hình lăng trụ được tạo từ hai mặt dưới là những đa giác song song và những mặt bên là những tứ giác .
- Hình lăng trụ đứng là hình lăng trụ có cách cạnh bên và những mặt dưới vuông góc với nhau .
- Các hình tròn trụ thường thấy trong đời sống như thể hộp sữa bột cho trẻ, những lon nước ngọt, hộp sữa đặc ông thọ, hay ly uống nước …
Tất cả những vật đều chiếm một khoảng chừng khoảng trống nhất định, khoảng chừng khoảng trống mà vật đó chiếm giữ chính là thể tích của vật đó. Thể tích hình tròn trụ là khoảng chừng khoảng trống đơn cử mà hình tròn trụ chiếm giữ. Để tính được thể tích của nó, ta cần vận dụng những công thức dưới đây .
Công thức tính thể tích các loại hình trụ
Thứ nhất, công thức tính thể tích hình tròn trụ tròn :
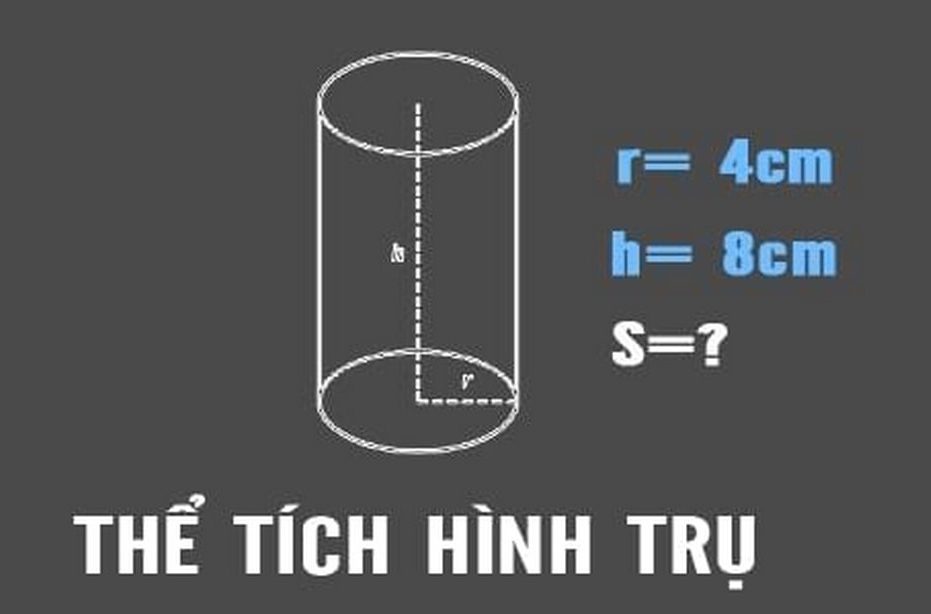
Thể tích của hình tròn trụ tròn được tính theo công thức : V = π x r2 x h. Trong đó : V là thể tích ; r là nửa đường kính của hình tròn trụ ; h là chiều cao hình tròn trụ ; π = 3.14 .
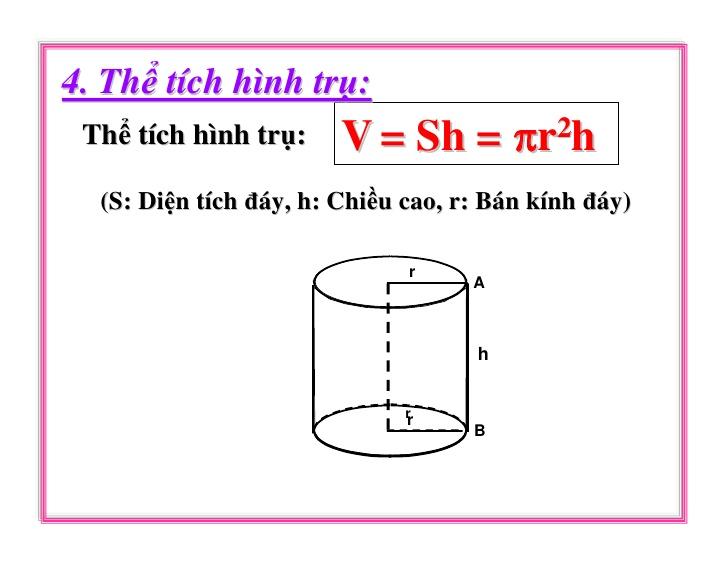
Công thức tính thể tích của hình tròn trụ tròn ( Nguồn : Internet )
Thứ hai, công thức tính thể tích khối lăng trụ :
Thể tích khối lăng trụ được tính theo công thức sau : V = B x h. Trong đó : V là thể tích của hình tròn trụ ; B là diện tích quy hoạnh dưới mặt đáy ; h là chiều cao giữa hai dưới mặt đáy .
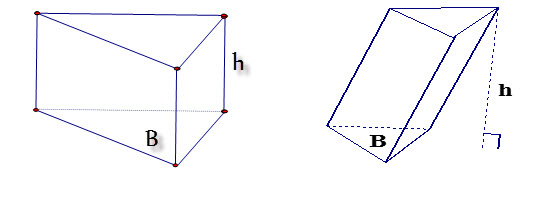
Thể tích của hình tròn trụ tam giác ( Nguồn : Internet )
Một số bài toán mẫu tính thể tích hình tròn trụ
Bài số 1: Cho một cái ca hình trụ tròn không nắp, có đường kính đáy bằng độ cao của cái ca là 10 cm. Hỏi cái ca đó đựng được bao nhiêu lít nước?
Cách giải :
Số lít nước mà cái ca đựng được chính là thể tích của cái ca .
Cái ca là một hình trụ tròn, vì vậy để tính số nước mà cái ca đựng được, chúng ta áp dụng công thức tính thể tích đối với hình trụ tròn: V = π x r2 x h
Xem thêm: Cách chứng minh đường trung trực lớp 7
Hình trụ có đường kính bằng 10 cm, như vậy nửa đường kính của hình tròn trụ là :
- 10 : 2 = 5 cm
Áp dụng công thức, ta được :
- V = π x r2 x h = 3.14 x 25 x 10 = 785 cm3cm3
Đổi từ cm3 ra lít ta được : 785 cm3cm3 = 0.785 dm3dm3 = 0.785 lít
Như vậy, cái ca hoàn toàn có thể đựng được 0.785 lít nước .
Bài số 2: Hãy tính thể tích V của khối lăng trụ tam giác đều ABC.A’B’C’ có các cạnh AA′=BC=a. AA′=BC=a. Hãy chọn đáp án đúng:
- A. V = a33 √ 12V = a3312
- B. V = a33 √ 4V = a334
- C. V = a32 √ 6V = a326
- D. V = a33
Theo đề bài, ta có hình vẽ :
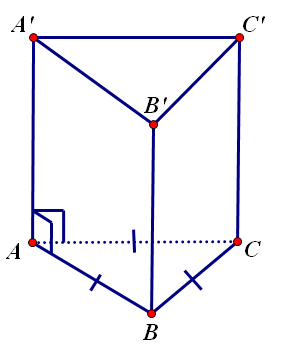
Tính thể tích V của khối lăng trụ tam giác đều ABC.A ’ B’C ’ ( Nguồn : Internet )
Cách giải :
Vì tam giác ABC là tam giác đều nên diện tích quy hoạnh của tam giác ABC là :
- S ( ABC ) = a23 √ 4 => S ( ABC ) = a234 .
Áp dụng công thức tính thể tích so với hình tròn trụ tam giác là V = B x h, ta có :
- V ( ABC.A ′ B ′ C ′ ) = SABC.AA ′ = a33 √ 4. VABC.A ′ B ′ C ′ = SABC.AA ′ = a334 .
Như vậy, đáp án đúng là đáp án D .
Trên đây là những kỹ năng và kiến thức cơ bản về khái niệm những loại hình trụ, những công thức cơ bản tính thể tích những loại hình trụ và những bài toán hướng dẫn chi tiết cụ thể cách tính thể tích để những bạn tìm hiểu thêm. Chúc những bạn học tốt !
Cách tính thể tích hình nón, hình chóp, hình chóp cụt: Dù bạn còn là học sinh hoặc ra trường rồi, thì việc nắm rõ cách tính thể tích hình nón sẽ là lợi thế rất lớn. Cùng tổng hợp lại các công thức quan trọng nhé!
: Dù bạn còn là học sinh hoặc ra trường rồi, thì việc nắm rõ cách tính thể tích hình nón sẽ là lợi thế rất lớn. Cùng tổng hợp lại các công thức quan trọng nhé!
Xem thêm: Cuộc sống vốn luôn chứa đựng những muộn phiền, cũng may còn có bầu trời luôn cho ta niềm tin!
Hướng dẫn tính diện tích mặt cầu, công thức và ví dụ chi tiết: Định nghĩa: Hình cầu là một vật thể hình tròn ba chiều hoàn hảo, mỗi điểm nằm trên bề mặt của nó đều có khoảng cách đến tâm bằng nhau.: Định nghĩa : Hình cầu là một vật thể hình tròn ba chiều hoàn hảo nhất, mỗi điểm nằm trên mặt phẳng của nó đều có khoảng cách đến tâm bằng nhau .
Source: http://139.180.218.5
Category: tản mạn