Trong chương trình toán 7 môn hình học, các bạn đã được học về đường trung tuyến và các tính chất, định lý của đường trung tuyến trong tam giác. Kiến thức này được củng cố lại ở lớp 10. Tuy nhiên, nhiều bạn đang bị lẫn lộn giữa khái niệm đường trung tuyến và đường trung trực. Vậy đường trung tuyến là gì? Hãy đọc bài viết dưới đây để có câu trả lời đầy đủ nhất về đường trung tuyến.

Đường trung tuyến là gì ?

Đường trung tuyến của đoạn thẳng

Đường trung tuyến của đoạn thẳng là đường thẳng đi qua trung điểm của đoạn thẳng đó

Đường trung tuyến của tam giác

Đường trung tuyến của tam giác là đoạn thẳng có một đầu là đỉnh của tam giác, đầu kia là trung điểm cạnh đối lập với đỉnh đó .

Mỗi tam giác bất kỳ đều có 3 đường trung tuyến.

Tam giác ABC có D là trung điểm của cạnh BC thì AD là một đường trung tuyến của tam giác ABC. Như vậy, nếu D, E, F lần lượt là trung điểm của ba cạnh BC, AC, AB. Thì AD, CE, BF là ba đường trung tuyến của tam giác ABC .

Công thức, đặc thù của đường trung tuyến trong tam giác

Tính chất đường trung tuyến trong tam giác thường

• Ba đường trung tuyến của một tam giác đồng quy tại một điểm, điểm đó được gọi là trọng tâm của tam giác.
• Trọng tâm của tam giác cách mỗi đỉnh một khoảng bằng 2/3 độ dài đường trung tuyến đi qua đỉnh ấy.
• Khoảng cách từ trọng tâm đến trung điểm của mỗi cạnh bằng 1/3 đường trung tuyến tương ứng với điểm đó.

Tính chất đường trung tuyến trong tam giác vuông

ABC vuông có AD là trung tuyến ứng với cạnh huyền BC
=> AD = 1/2 BC = DB = DC
trái lại, nếu trung tuyến AM = 1/2 BC thì ABC vuông tại A

Tính chất:

• Trong tam giác vuông, trung tuyến ứng với cạnh huyền bằng 1/2 cạnh huyền.
• Một tam giác có trung tuyến ứng với một cạnh bằng nửa cạnh đó thì tam giác ấy là tam giác vuông.
• Đường trung tuyến của tam giác vuông có đầy đủ các tính chất của một đường trung tuyến tam giác.

Tính chất đường trung tuyến trong tam giác cân

ABC cân tại A có đường trung tuyến AD ứng với cạnh BC => AD ⊥ BC và ΔADB = ΔADC

Tính chất:

• Đường trung tuyến ứng với cạnh đáy thì vuông góc với cạnh đáy. Và chia tam giác thành 2 tam giác bằng nhau.

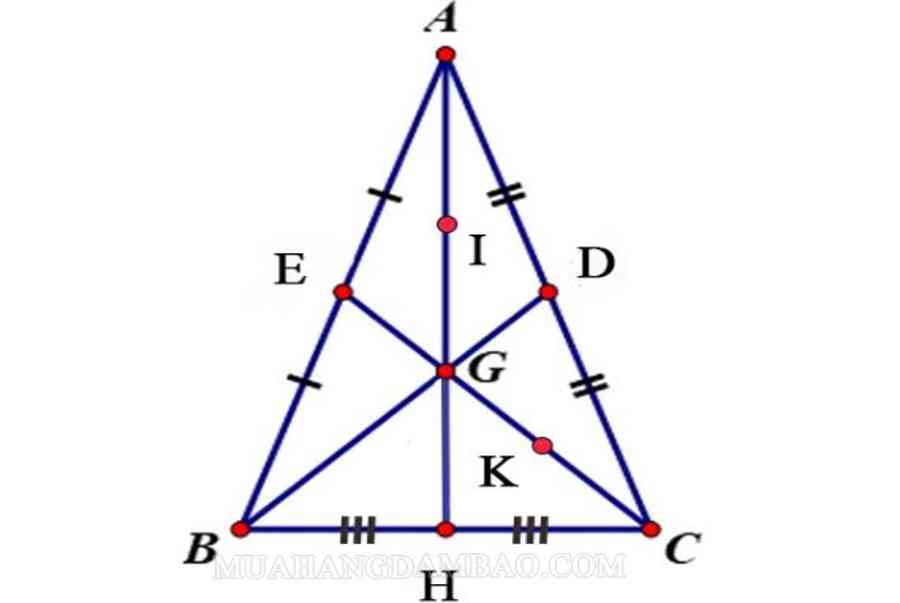
Tính chất đường trung tuyến trong tam giác đều

ΔABC đều => ΔGAE = ΔGAF = ΔGCF = ΔGCD = ΔGBD = ΔGBE = ΔGEB = ΔGEA
SADB = SADC = SCEA = SCEB = SBFA = SBFC

Tính chất:

• 3 đường trung tuyến của tam giác đều sẽ chia tam giác đó thành 6 tam giác có diện tích bằng nhau.
• Trong tam giác đều đường thẳng đi qua một đỉnh bất kỳ và đi qua trọng tâm của tam giác sẽ chia tam giác đó thành 2 tam giác có diện tích bằng nhau.

Công thức độ dài của đường trung tuyến

Độ dài đường trung tuyến của một tam giác được tính trải qua độ dài những cạnh của tam giác và được tính bằng định lý Apollonnius :

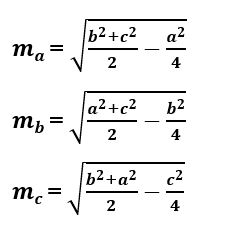
Với ma là trung tuyến ứng với cạnh a trong tam giác
mb là trung tuyến ứng với cạnh b trong tam giác
mc là trung tuyến ứng với cạnh c trong tam giác
Trong đó :

• a, b, c: là các cạnh của tam giác.
• ma, mb, mc: là các đường trung tuyến của tam giác.

Các dạng bài tập về đường trung tuyến thường gặp

Dạng 1 : Tìm những tỉ lệ giữa những cạnh, tính độ dài đoạn thẳng

Phương pháp:

Chú ý đến vị trí trọng tâm của tam giác
Với G là trọng tâm của tam giác ABC và AB, BE, CF là 3 đường trung tuyến, ta có
AG = 2/3 AD ; BG = 2/3 BE ; CG = 2/3 CF

Dạng 2 : Đường trung tuyến với những tam giác đặc biệt quan trọng ( tam giác vuông, tam giác cân, tam giác đều )

Phương pháp:

Trong tam giác cân ( hoặc tam giác đều ), trung tuyến ứng với cạnh đáy và chia tam giác thành hai tam giác bằng nhau .

Bài tập ví dụ về đường trung tuyến trong tam giác

Bài 1: Cho tam giác ABC cân ở A có AB = AC = 17cm, BC= 16cm. Kẻ trung tuyến AM.

• a) Chứng minh: AM ⊥ BC;
• b) Tính độ dài AM.

Lời giải :

a. Ta có AM là đường trung tuyến ABC nên MB = MC
Mặt khác ABC cân tại A
=> AM vừa là đường trung tuyến vừa là đường cao
Vậy AM ⊥ BC
b. Ta có
BC = 16 cm nên BM = MC = 8 cm
AB = AC = 17 cm
Xét tam giác AMC vuông tại M
Áp dụng Định lý Pitago có :
AC2 = AM2 + MC2 => 172 = AM2 + 82 => AM2 = 172 – 82 = 225 => AM = 15C m .

Bài 2: Cho G là trọng tâm của tam giác đều ABC. Chứng minh rằng GA = GB = GC.

Bài giải: 

Gọi AD, CE, BF là những đường trung tuyến tam giác ABC hay D, E, F lần lượt là trung điểm cạnh BC, AB, AC

Ta có AD là đường trung tuyến tam giác ABC nên AG = 2/3 AD ( 1 )
CE là đường trung tuyến tam giác ABC nên CG = 2/3 CE ( 2 )
BF là đường trung tuyến tam giác ABC nên BG = 2/3 BF ( 3 )
Ta có ΔBAC đều => AD = BF = CE ( 4 )
Từ ( 1 ), ( 2 ), ( 3 ), ( 4 ) suy ra AG = BG = CG

Bài 3: Cho tam giác ABC. D thuộc tia đối của tia AB  sao cho  AD = AB. Trên cạnh AC lấy điểm E sao cho AE =1/3AC. Tia BE cắt CD ở M. Chứng minh :

• a) M là trung điểm của CD
• b) AM = 12BC.

Bài giải: Ta có hình vẽ:

a, Xét : ΔBDC có AB = AD suy ra AC là đường trung tuyến tam giác BCD
Mặt khác :
AE = 1/3 AC => CE = 2/3 AC .
=> E là trọng tâm Δ BCD
M là giao của BE và CD
Vậy BM là trung tuyến Δ BCD
Vậy M là trung điểm của CD
b, A là trung điểm của BD
M là trung điểm của DC
=> AM là đường trung bình của Δ BDC
=> AM = 1/2 BC

Bài 4: Cho tam giác ABC vuông ở A, có AB = 18cm, AC = 24cm, trọng tâm G. Tính tổng khoảng cách từ điểm G đến các đỉnh của tam giác.

Bài giải: ta có hình vẽ:

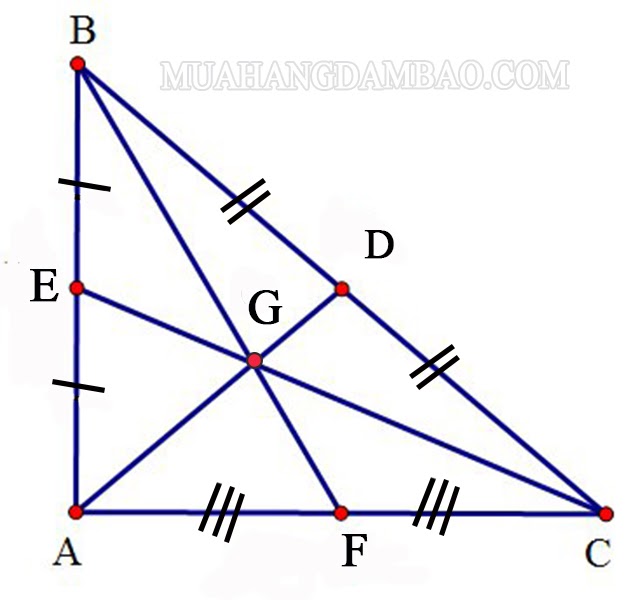
Gọi AD, CE, BF lần lượt là những đường trung tuyến nối từ đỉnh A, C, B của tam giác ABC
Dễ dàng suy ra AE = EB = 9 cm, AF = FC = 12 cm
Ta có tam giác ABC vuông tại A, vận dụng định lý Pitago ta có
BC2 = AB2 + AC2 => BC2 = 182 + 242 = 900 => BC = 30
Ta có ABC vuông mà D là trung điểm cạnh huyền nên AD = BD = DC = 15 cm
Suy ra AG = 2/3 AD = 10 cm
Xét Δ AEC vuông tại A, vận dụng định lý Pitago ta có :
EC2 = AE2 + AC2 => EC2 = 92 + 242 = 657 => EC = 3 √ 73 cm => CG = 2/3 EC = 2 √ 73 cm
Tương tự, xét AFB vuông tại A, vận dụng định lý Pitago ta có :
BF2 = AB2 + AF2 => BF2 = 182 + 122 = 468 => BF = 6 √ 13 cm => BG = 2/3 BF = 4 √ 13 cm
Tổng khoảng cách từ trọng tâm G đến những đỉnh của tam giác là :
AG + BG + CG = 10 + 4 √ 13 + 2 √ 73 cm

Bài 5: Cho tam giác ABC cân tại A, hai đường trung tuyến BD và CE cắt nhau tại G. Kéo dài AG cắt BC tại H.

• a, So sánh tam giác AHB và tam giác AHC
• b, Gọi Kvà I lần lượt là trung điểm của GC và GA. Chứng minh rằng AK, BD, CI đồng quy

Bài giải: Ta có hình vẽ:

a, Ta có BD là đường trung tuyến của tam giác ABC
CE là đường trung tuyến của tam giác ABC
Vậy G là trọng tâm tam giác ABC
Mà AH đi qua G nên AH là đường trung tuyến của tam giác ABC
=> HB = HC
Xét ΔAHB và Δ AHC có :
AB = AC ( ABC cân tại A )
AH chung
HB = HC
=> Δ AHB = ΔAHC ( c-c-c )
b, Ta có IG = IA nên CI là đường trung tuyến của ΔAGC ( 1 )
Lại có KC = KG nên AK là đường trung tuyến của ΔAGC ( 2 )
DG là đường trung tuyến của AGC ( 3 )
Từ ( 1 ), ( 2 ), ( 3 ) suy ra 3 đường trung tuyến AK, CI, DG đồng quy tại I

Thông qua bài viết này, kỳ vọng những bạn đã nắm được kiến thức và kỹ năng về đường trung tuyến, đặc thù của nó để vận dụng vào giải bài tập nhanh và đúng mực nhất .

Source: http://139.180.218.5
Category: tản mạn