Bộ môn toán hình học luôn mang lại cho chúng ta cảm giác cực kỳ thú vị. Tuy nhiên việc ghi nhớ các công thức hay phân biệt tính chất cũng khiến nhiều học sinh ngán ngẩm. Đừng quá lo lắng nhé! Toppy sẽ đồng hành cùng bạn trong từng bài học. Hôm nay, chúng ta hãy cùng ôn tập các kiến thức quan trọng của tính chất ba đường trung trực của tam giác thôi nào!
Nội dung chính
Đường trung trực của tam giác là gì?
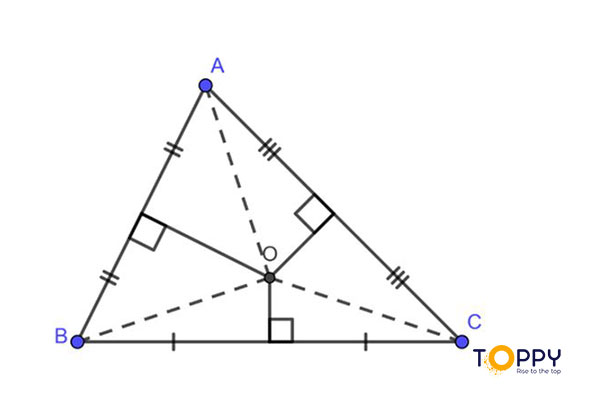
- Định nghĩa vềđường trung trực
của tam giác được phát biểu như sau: “Trong một tam giác, đường trung trực của mỗi cạnh gọi là đường trung trực của tam giác đó.”
Chẳng hạn như trong tam giác ABC : a là đường trung trực ứng với cạnh BC, b là đường trung trực ứng với cạnh AC và c là đường trung trực ứng với cạnh AB.
- Trong mỗi tam giác đều có ba đường trung trực .
- Tính chất của đường trung trực : Trong một tam giác cân, đường trung trực của cạnh đáy đồng thời là đường trung tuyến ứng với cạnh này .
Tính chất ba đường trung trực của tam giác
Tính chất ba đường trung trực của tam giác đơn cử như sau :
- Bất kỳ tam giác nào cũng được chiếm hữu 3 đường trung trực, đặc thù chung của 3 đường này như sau : Cùng đi qua một điểm, điểm này cách đều ba đỉnh của tam giác đó .
Chẳng hạn như : O là giao điểm ba đường trung trực của tam giác ABC, suy ra ta có OA = OB = OC
- Lưu ý : nếu một đường tròn lấy giao điểm của 3 đường trung trực làm tâm và đi qua 3 đỉnh của tam giác, thì đường tròn đó được gọi là đường tròn ngoại tiếp tam giác .
Chẳng hạn như : O là giao điểm của 3 đường trung trực tam giác ABC và một đường tròn tâm O đi qua ba đỉnh A, B, C ; thì đường tròn đó là đường tròn ngoại tiếp tam giác ABC .
Để hiểu rõ hơn về tính chất đường trung trực của một tam giác, có thể tìm đọc thêm 1 số bài viết khác của Toppy.
>> Xem thêm : Tính chất đường trung trực của một đoạn thẳng
Một số bài tập trắc nghiệm ứng dụng tính chất ba đường trung trực của tam giác

Bài tập 1
Cho ΔABC có hai đường cao BD và CE, gọi M là trung điểm của BC. Em hãy chọn câu sai :
- BM = MC
- ME = MD
- DM = MB
- M không thuộc đường trung trực của cạnh DE
- Ta có : M là trung điểm của BC, suy ra theo đặc thù trung điểm thì BM = MC, loại đáp án A .
- Xét ΔBCE có M là trung điểm của BC. Suy ra EM chính là trung tuyến
Ta có triết lý : Trong tam giác vuông, đường trung tuyến ứng với cạnh huyền bằng nửa cạnh đó. ⇒ EM = BC / 2 ( 1 )
- Tiếp tục xét ΔBCD có M là trung điểm của BC. Suy ra DM cũng là trung tuyến
⇒ DM = MB = BC / 2 ( 2 ), nên loại đáp án C
Từ ( 1 ) và ( 2 ) suy ra : EM = DM ⇒ M thuộc đường trung trực của DE, loại được đáp án D, chọn đáp án B .
Bài tập 2
Cho ΔABC có AC > AB, tại AC lấy điểm E sao cho CE = AB, O là giao điểm của những đường trung trực của BE và AC. Chọn đáp án đúng :
- ΔABO = ΔCOE
- ΔBOA = ΔCOE
- ΔAOB = ΔCOE
- ΔABO = ΔCEO
Xét tam giác ΔAOB và ΔCOE ”
- O thuộc đường trung trực của AC ⇒ OA = OC
- O thuộc đường trung trực của BE ⇒ OB = OE
- Theo giả thiết : AB = CE
Do đó ΔAOB = ΔCOE ( cạnh-cạnh-cạnh )
Chọn đáp án C
Bài tập 3
Cho ΔABC vuông tại A có đường cao AH, tại cạnh AC lấy điểm K sao cho AK = AH, KD ⊥ AC ( D ∈ BC ). Chọn câu đúng
- ΔAHD = ΔAKD
- AD là đường trung trực của HK
- AD là tia phân giác của góc HAK
- Cả A, B, C đều đúng
Xét tam giác vuông AHD và AKD có :
- AH = AK ( giả thiết )
- AD chung
Suy ra ΔAHD = ΔAKD ( cạnh huyền-cạnh góc vuông ) nên câu A đúng
Ta có : HD = DK ; ∠ HAD = ∠ DAK.
Suy ra AD là tia phân giác của góc HAK, nên câu C đúng
Ta lại có : AH = AK ( gỉa thiết ) và HA = DK ( cmt ). Suy ra AD là đường trung trực của đoạn thẳng HK nên B đúng .
Vậy A, B, C đều đúng. Chọn đáp án D
Một số bài tập tự luận ứng dụng tính chất ba đường trung trực của tam giác
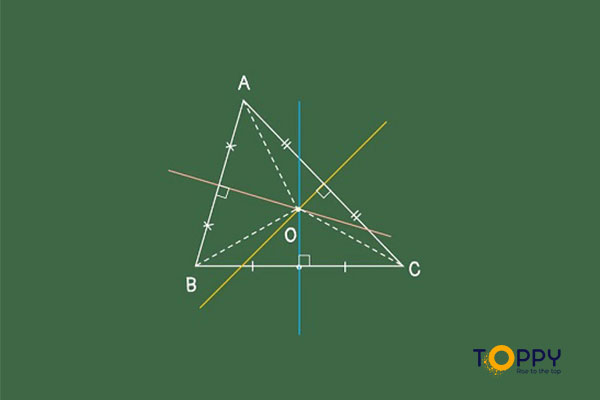
Bài tập 1
Cho tam giác ABC, AK là đường phân giác của góc A, giao điểm đường phân giác của tam giác ABK trùng với giao điểm ba đường trung trực của tam giác ABC. Yêu cầu : Tính số đo những góc của tam giác ABC .
Bài giải:
Gọi O là giao điểm của 3 đường phân giác của tam giác ABC, O là giao điểm của ba đường trung trực của tam giác ABC ( giả thiết )
Suy ra :
- OA = OB = OC
- Các tam giác AOB, AOC, BOC là những tam giác đều .
AK là đường phân giác của góc BAC ( giả thiết ). Suy ra : nếu ∠ KAB = 2 x thì ∠ BAC = 4 x
Ta có : ΔAOB = ΔCOB. Suy ra : AB = CB
Vậy tam giác ABC cân tại đỉnh B
⇒ ∠ BAC = ∠ BCA
Khi đó ta có :
2 x + 4 x + 4 x = 180 ° ⇒ 10 x = 180 ° ⇒ x = 18 °
Vậy hoàn toàn có thể Tóm lại số đo những góc của tam giác ABC là : ∠ A = ∠ C = 72 °, ∠ B = 18 °
Bài tập 2
Cho tam giác đều ABC, tại ba cạnh AB, BC và CA lấy những điểm theo thứ tự M, N, P. sao cho AM = BN = CP., O là giao điểm của ba đường trung trực. Yêu cầu : Chứng minh O cũng là giao điểm ba đường trung trực của tam giác MNP .
Bài giải :
O là giao điểm của ba đường trung trực của tam giác ABC ( giả thiết ). Suy ra : OA = OB = OC ⇒ Các tam giác AOM, BON, COP có :
AM = BN = CP ( gt )
Do đó : ΔAOM = ΔBON = ΔCOP ( cạnh-góc-cạnh )
⇒ OM = ON = OP
Hay nói cách khác : O là giao điểm của ba đường trung trực tam giác MNP
Trên đây là một số kiến thức lý thuyết và bài tập về tính chất ba đường trung trực của tam giác mà chúng tôi muốn chia sẻ đến các bạn. Hy vọng các bạn đã có những phút giây học tập thật bổ ích với Toppy!
Xem ngay:
Source: http://139.180.218.5
Category: tản mạn
