Hàm số chẵn, hàm số lẻ được đưa vào giảng dạy từ chương trình đại số lớp 10. Bài viết này đề cập đến tính chất của nó để ứng dụng vào giải các bài toán hàm số ở lớp 12. Hy vọng bài viết sẽ cung cấp cho các em học sinh lớp 12 đang ôn thi THPTQG thêm một cách để giải quyết các bài toán hàm số một cách nhanh nhất có thể.
Trước hết hiểu một cách trực quan thì hàm số chẵn hay lẻ là có đồ thị nhận trục tung là trục đối xứng (chẵn) hoặc đồ thị nhận gốc tọa độ là tâm đối xứng (lẻ).
Do đó tập xác định của chúng cũng phải đối xứng qua điểm x=0. Tức là với mọi số thuộc tập xác định của hàm số thì số đối của nó cũng thuộc tập xác định của hàm số.
Chẳng hạn:
Tập số (−1;1) đối xứng qua điểm x=0.
Tập số [−1;1) không đối xứng qua điểm x=0.
Nội dung chính
ĐỊNH NGHĨA HÀM SỐ CHẴN HÀM SỐ LẺ
a. Hàm số chẵn là gì
Hàm số chẵn có đồ thị đối xứng qua trục tung. Do đó nếu lấy một điểm bất kỳ (x;f(x)) trên đồ thị thì nó phải có một ” người anh em” phía bên kia trục tung là điểm (-x;f(−x)) và dĩ nhiên f(−x)=f(x).
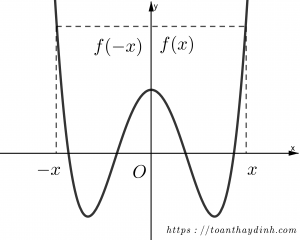
Vậy điều kiện cần và đủ để hàm số f(x) xác định trên D là hàm số chẵn là
∀x∈D thì −x∈D và ∀x∈D thì f(−x)=f(x)
b. Hàm số lẻ là gì
Hàm số lẻ có đồ thị đối xứng qua gốc tọa độ. Do đó nếu lấy một điểm bất kỳ (x;f(x)) trên đồ thị thì nó phải có “một người chị em” đối xứng qua gốc tọa độ là điểm (−x;f(−x)).
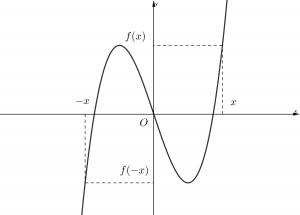
Vì hai điểm đó đối xứng với nhau qua gốc tọa độ nên f ( − x ) = − f ( x ) .
Vậy điều kiện kèm theo cần và đủ để hàm số f ( x ) xác lập trên D là hàm số chẵn là
∀x∈D thì −x∈D và ∀x∈D thì f(−x)=−f(x)
Hàm số không chẵn không lẻ là như thế nào?
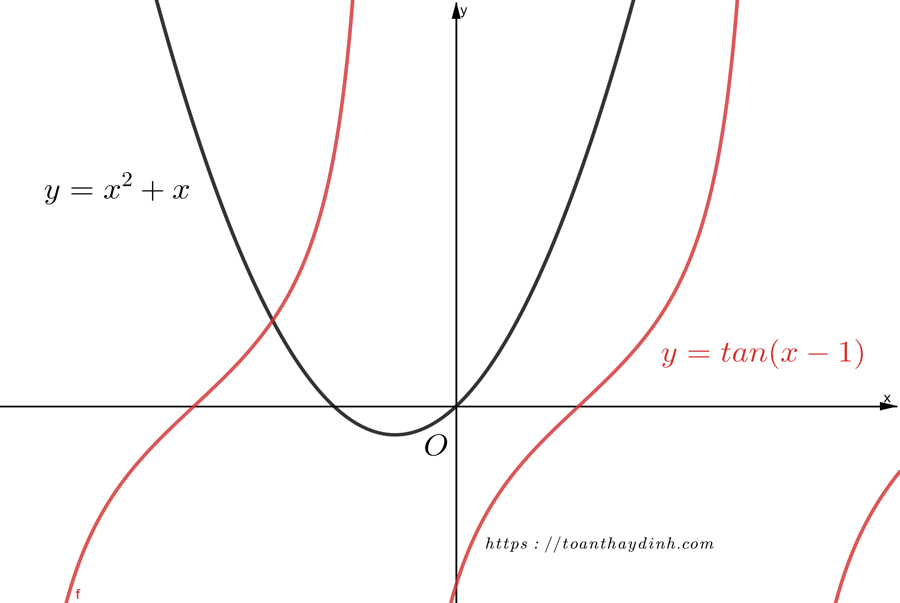
Cuộc đời không như là mơ. Không phải ai sinh ra cũng hoàn hảo :)). Hàm số cũng vậy. Có những hàm số không phải hàm chẵn, cũng chẳng phải hàm lẻ. Chẳng hạn như hàm số y=x²+x, y=tan(x-1),… là những hàm số như vậy.
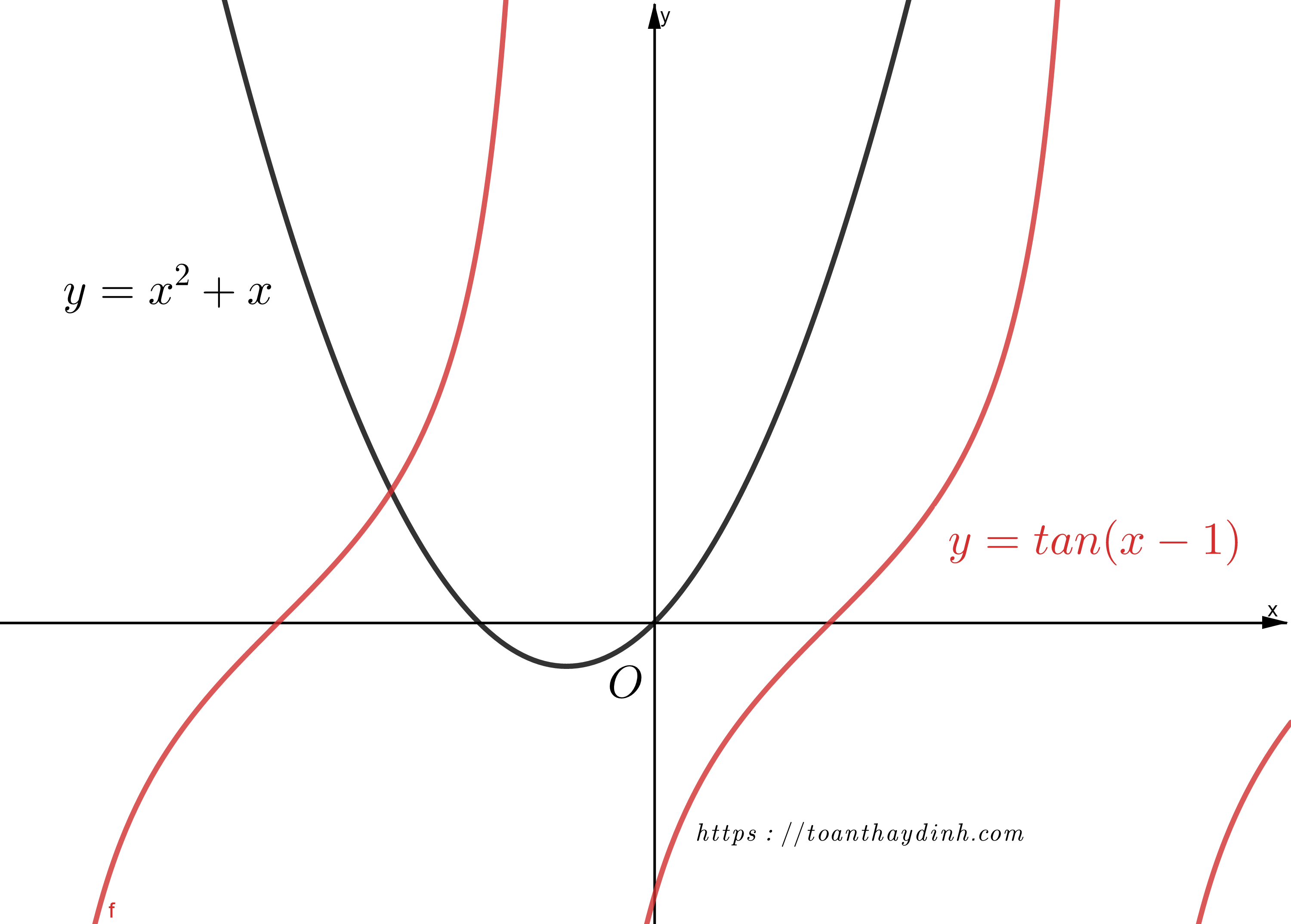
Chú ý : Nếu hàm số vừa chẵn vừa lẻ thì nó là hàm số y=0.
XÁC ĐỊNH TÍNH CHẴN LẺ CỦA HÀM SỐ
Sau đây là một số ít gợi ý cách xác lập hàm số chẵn lẻ để tất cả chúng ta hoàn toàn có thể xét một cách nhanh gọn :
a. Nhớ một số ít hàm số chẵn lẻ thường gặp
Hàm số chẵn lẻ thường gặp trong giải toán
+y=ax+b là hàm số lẻ khi và chỉ khi b=0.
+ y=ax²+bx+c là hàm số chẵn khi và chỉ khi b=0.
+ y=ax³+bx²+cx+d là hàm số lẻ khi và chỉ khi b=d=0.
+Hàm trùng phương bậc bốn là hàm số chẵn.
+ y=sinx, y=tanx, y=cotx là các hàm số lẻ. Xem thêm tại đây.
+ y=cosx là hàm số chẵn.
+Hàm y=f(|x|) là hàm số chẵn.
+Nếu f(x) là hàm số chẵn và có đạo hàm trên tập xác định thì f'(x) là hàm lẻ.
+Nếu f(x) là hàm số lẻ và có đạo hàm trên tập xác định thì f'(x) là hàm chẵn.
+Hàm số đa thức bậc chẵn thì không thể là hàm số lẻ.
+Hàm số đa thức bậc lẻ thì không thể là hàm số chẵn.
b. Nhận dạng hàm số chẵn lẻ dựa vào đồ thị hàm số
Như tất cả chúng ta đã biết, đồ thị hàm số chẵn ( lẻ ) đối xứng qua trục tung ( gốc tọa độ ) nên ta hoàn toàn có thể nhận dạng trải qua việc quan sát đồ thị hàm số .
c. Sử dụng định nghĩa
Cách này thường Open trong xét tính chẵn lẻ của hàm số lop 10 .
Thông thường để sử dụng định nghĩa ta chia làm hai bước như sau :
− Đầu tiên ta kiểm tra tập xác lập của hàm số có đối xứng hay không. Nếu tập xác lập đối xứng ta triển khai bước thức hai. Nếu tập xác lập không đối xứng thì ta Kết luận rằng hàm không chẵn không lẻ .
− Bước thứ hai ta biến hóa biểu thức f ( – x ) nhằm mục đích so sánh với biểu thức f ( x ). Nếu hai biểu thức giống hệt ta Tóm lại đó là hàm số chẵn. Còn hai biểu thức đối nhau ta Kết luận đó là hàm số lẻ. Không so sánh được ta tìm một giá trị x để f ( x ) và f ( – x ) không đối cũng không bằng nhau và từ đó Kết luận .
Ví dụ : Chứng minh rằng hàm số f ( x ) = x³ + x là hàm số lẻ .
Lời giải :
Tập xác lập : R
Với mọi số thực x ta có : f ( − x ) = ( − x ) ³ + ( − x ) = − ( x³ + x ) = − f ( x ) .
Do đó hàm số đã cho là hàm số lẻ .
d. Cách xác lập hàm số chẵn lẻ bằng máy tính
Ý tưởng sử dụng Casio để xét dựa trên giá trị f ( x ) và f ( – x ) bằng nhau hoặc đối nhau. Để triển khai ta sử dụng tính năng Table ở chính sách hai hàm số .
Ví dụ : Xét tính chẵn lẻ của hàm số y = x³ + 2 x² – 3
Giải : Trên máy tính cầm tay Vinacal 570 ES Plus II ta bấm như sau ( những máy tính bỏ túi khác bấm tựa như ) :
MODE 7
Ta thực thi nhập hàm số đã cho trong đề bài
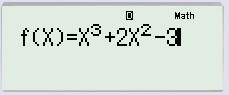
Tiếp theo ta nhập hàm số g ( x ) = f ( − x ) ( Tức là vị trí nào của x ta bấm − x )
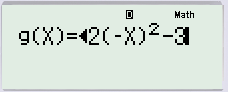
Các mục tiếp theo là START, END, STEP ta để mặc định cho nhanh ( hoàn toàn có thể chọn cũng được ). Ta được tác dụng như sau :
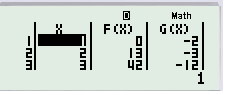
Đến đây ta dò hai cột giá trị F ( X ) và G ( X ) thì thấy rằng tại x = 1 hai giá trị không bằng nhau cũng không đối nhau. Do đó hàm đã cho không phải hàm chẵn cũng không phải hàm lẻ. Lưu ý giải pháp này mang tính ước đạt và không thay thế sửa chữa cho chứng tỏ được. Tuy nhiên sử dụng trong giải toán trắc nghiệm hoàn toàn có thể sử dụng được .
ỨNG DỤNG VÀO ÔN THI THPT QG
Có nhiều bài toán của lớp 12, tất cả chúng ta hoàn toàn có thể khai thác xét tính chẵn lẻ để xử lý nhanh hơn cách giải thường thì .
Ví dụ: Cho hàm số f(x) liên tục trên R, f'(x) có đồ thị như hình vẽ. Hàm số f(|x|)+2020 đồng biến trên khoảng nào trong các khoảng sau đây?
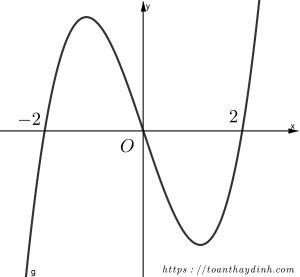
A. (−∞;−2).
B. ( – 2 ; 0 ) .
C. ( − 2 ; 2 )
D. ( 0 ; + ∞ ) .
Lời giải:
Nhận xét f ‘ ( x ) là hàm lẻ nên f ( x ) là hàm chẵn .
Sự biến thiên của f ( | x | ) + 2020 so với hàm số f ( x ) là không đổi .
Vậy ta chọn phương án B.
BÀI TẬP TỰ LUYỆN
Câu 1: Trong các hàm số sau, hàm số nào là hàm số lẻ?
A. y = sin ( x + 1 ) .
B. y = − 4 x³ + 3 x² + 2 x – 5 .
C. y = 2 | x | ³ + 2 x² + | x | – 4 .
D. y = x² + 3 .
Câu 2: Có bao nhiêu giá trị nguyên dương của tham số m để hàm số
y = x² + 2 ( m²-4 ) x + 3 m – 2
là hàm số chẵn ?
A. 0 .
B. 1 .
C. 2 .
D. 3 .
Câu 3: Gọi S là tập hợp tất cả các giá trị của tham số m để hàm số y=2x³-2(m²-1)x²+4x+m-1 là hàm số lẻ. Số phần tử của S là
A. 0 .
B. 1 .
C. 2 .
D. 3 .
Câu 4: Cho f(x) là hàm số chẵn có bảng biến thiên như hình vẽ
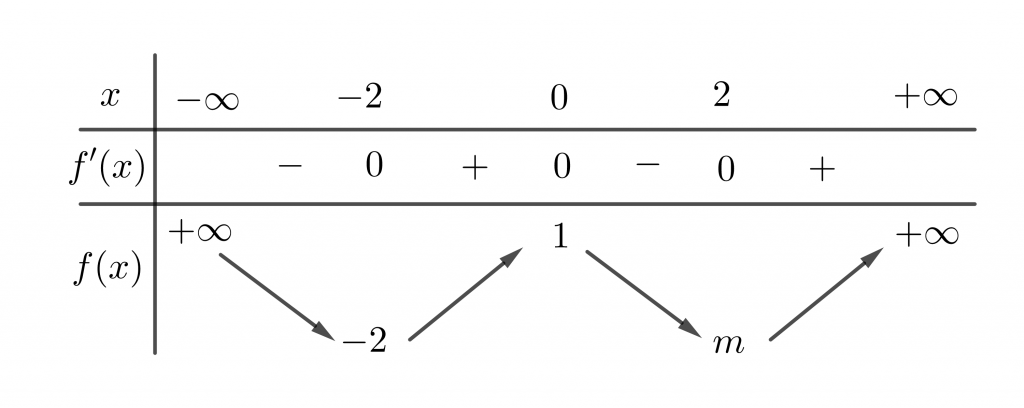
Giá trị lớn nhất của hàm số g(x)=f(|x|) trên đoạn [-1;2] là
A. 1 .
B. 2 .
C. − 1 .
D. 0 .
Câu 5: Cho hàm số f(x) xác định và liên tục trên R có 5 điểm cực trị dương và f'(0)≠0. Số cực trị của hàm số f(|x|) là
A. 5 .
B. 10 .
C. 11 .
D. 12 .
Chúc các em thành công và may mắn!!!
Xem thêm:
Xét tính chẵn lẻ của hàm số lượng giác
Hàm số bậc nhất bậc 2 –
Source: http://139.180.218.5
Category: Thuật ngữ đời thường