Tính Khoảng Cách Từ 1 Điểm Đến 1 Mặt Phẳng Trong Không Gian, Khoảng Cách Từ 1 Điểm Đến Mặt Phẳng Trong Oxyz

Ở các lớp trước các em đã làm quen với khái niệm khoảng cách từ điểm tới mặt phẳng trong không gian. Ở chương trình toán 12 với không gian tọa độ, việc giám sát khoảng cách được cho là khá dễ với nhiều em, tuy nhiên đừng vì vậy mà các em chủ quan nhé .
Đang xem : Tính khoảng cách từ 1 điểm đến 1 mặt phẳng trong không gian

Bài viết dưới đây chúng ta cùng ôn lại cách tính khoảng cách từ điểm tới mặt phẳng trong không gian tọa độ Oxyz. Đồng thời qua đó giải các bài tập vận dụng để các em dễ dàng ghi nhớ công thức hơn.

I. Công thức cách tính khoảng cách từ điểm đến mặt phẳng trong Oxyz

– Trong không gian Oxyz, để tính khoảng cách từ điểm M ( xM, yM, zM ) đến mặt phẳng ( α ) : Ax + By + Cz + D = 0, ta dùng công thức :

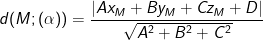
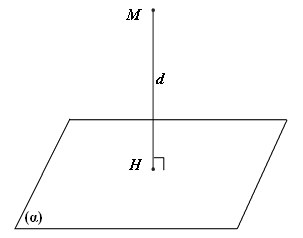
II. Bài tập vận dụng tính khoảng cách từ điểm tới mặt phẳng trong không gian tọa độ Oxyz

* Bài 1 (Bài 9 (trang 81 SGK Hình học 12): Tính khoảng cách từ điểm A(2; 4; -3) lần lượt đến các mặt phẳng sau:

a ) 2 x – y + 2 z – 9 = 0 ( α )
b ) 12 x – 5 z + 5 = 0 ( β )
c ) x = 0 ( γ ; )

* Lời giải:

a ) Ta có : Khoảng cách từ điểm A tới mp ( α ) là :

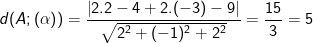
b ) Ta có : Khoảng cách từ điểm A tới mp ( β ) là :

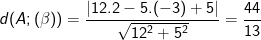
c ) Ta có : khoảng cách từ điểm A tới mp ( γ ) là :

* Bài 2: Cho hai điểm A(1;-1;2), B(3;4;1) và mặt phẳng (P) có phương trình: x + 2y + 2z – 10 = 0. Tính khoảng cách từ A, B đến mặt phẳng (P).

* Lời giải:

– Ta có :


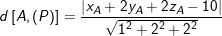
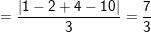
– Tương tự :

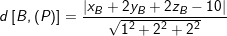
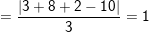
* Bài 3: Tính khoảng cách giữa hai mặt phẳng song song (P) và (Q) cho bởi phương trình sau đây :

( P ) : x + 2 y + 2 z + 11 = 0 .
( Q. ) : x + 2 y + 2 z + 2 = 0 .

* Lời giải:

– Ta lấy điểm M ( 0 ; 0 ; – 1 ) thuộc mặt phẳng ( P ), kí hiệu d là khoảng cách giữa hai mặt phẳng ( P ) và ( Q. ), ta có :

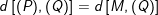
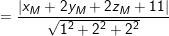
⇒ d = 3 .

* Bài 4: Tìm trên trục Oz điểm M cách đều điểm A(2;3;4) và mặt phẳng (P): 2x + 3y + z – 17 = 0.

* Lời giải:

– Xét điểm M ( 0 ; 0 ; z ) ∈ Oz, ta có :
– Điểm M cách đều điểm A và mặt phẳng ( P ) là :

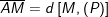
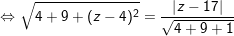
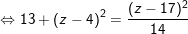
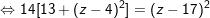
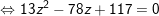
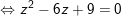
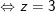
⇒ Vậy điểm M ( 0 ; 0 ; 3 ) là điểm cần tìm .

* Bài 5: Cho hai mặt phẳng (P1) và (P2) lần lượt có phương trình là (P1): Ax + By + Cz + D = 0 và (P2): Ax + By + Cz + D” = 0 với D ≠ D”.

Xem thêm : Đồ Án Voip Và Ứng Dụng – Đồ Án Chuyên Ngành Thiết Lập Tổng Đài Voip
a ) Tìm khoảng cách giữa hai mặt phẳng ( P1 ) và ( P2 ) .
b ) Viết phương trình mặt phẳng song song và cách đều hai mặt phẳng ( P1 ) và ( P2 ) .
* Áp dụng cho trường hợp đơn cử với ( P1 ) : x + 2 y + 2 z + 3 = 0 và ( P2 ) : 2 x + 4 y + 4 z + 1 = 0 .

* Lời giải:

a ) Ta thấy rằng ( P1 ) và ( P2 ) song song với nhau, lấy điểm M ( x0 ; y0 ; z0 ) ∈ ( P1 ), ta có :
Ax0 + By0 + Cz0 + D = 0 ⇒ ( Ax0 + By0 + Cz0 ) = – D ( 1 )
– Khi đó, khoảng cách giữa ( P1 ) và ( P2 ) là khoảng cách từ M tới ( P2 ) :

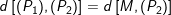
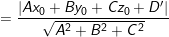
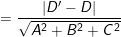
( theo ( 1 ) )
b ) Mặt phẳng ( P ) song song với hai mặt phẳng đã cho sẽ có dạng ( P ) : Ax + By + Cz + E = 0. ( 2 )
– Để ( P ) cách đều hai mặt phẳng ( P1 ) và ( P2 ) thì khoảng cách từ M1 ( x1 ; y1 ; z1 ) ∈ ( P1 ) đến ( P ) bằng khoảng cách từ M2 ( x2 ; y2 ; z2 ) ∈ ( P2 ) đến ( P ) nên ta có :

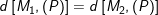
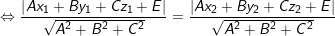
( 3 )
mà ( Ax1 + By1 + Cz1 ) = – D ; ( Ax2 + By2 + Cz2 ) = – D ” nên ta có :
( 3 )

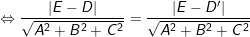
vì E ≠ D, nên :

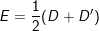
⇒ Thế E vào ( 2 ) ta được phương trình mp ( P ) : Ax + By + Cz + ½ ( D + D ” ) = 0

* Áp dụng cho trường hợp cụ thể với (P1): x + 2y + 2y + 3 = 0 và (P2): 2x + 4y + 4z + 1 = 0.

a ) Tính khoảng cách giữa ( P1 ) và ( P2 ) :
– mp ( P2 ) được viết lại : x + 2 y + 2 z + ½ = 0

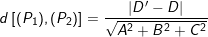
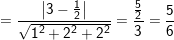
b ) Ta hoàn toàn có thể sử dụng 1 trong 3 cách sau :

– Cách 1: áp dụng kết quả tổng quát ở trên ta có ngay phương trình mp(P) là:

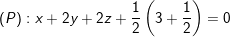
– Cách 2: (Sử dụng phương pháp qũy tích): Gọi (P) là mặt phẳng cần tìm, điểm M(x; y; z) ∈ (P) khi:

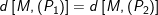
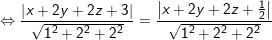
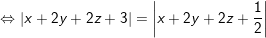
– Cách 3: (Sử dụng tính chất): Mặt phẳng (P) song song với hai mặt phẳng đã cho sẽ có dạng:

( P ) : x + 2 y + 2 z + D = 0 .
+ Lấy các điểm

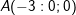
∈ ( P1 ) và

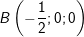
∈ ( P2 ), suy ra đoạn thẳng AB có trung điểm là

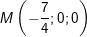
+ Mặt phẳng ( P ) cách đều ( P1 ) và ( P2 ) thì ( P ) phải đi qua M nên ta có :

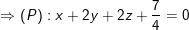
* Bài 6: Trong không gian Oxyz, cho điểm I(1;4;-6) và mặt phẳng (α): x – 2y + 2z + 4 = 0. Viết phương trình mặt cầu (S) có tâm I và tiếp xúc với mặt phẳng (α).

* Lời giải:

– Phương trình mặt cầu tâm I ( xi ; yi ; zi ) nửa đường kính R có dạng :
( x – xi ) 2 + ( y – yi ) 2 + ( z – zi ) 2 = R2
– Nên theo bài ra I ( 1 ; 4 ; – 6 ) pt mặt cầu ( S ) có dạng :
( x – 1 ) 2 + ( y – 4 ) 2 + ( z + 6 ) 2 = R2
– Vì mặt cầu ( S ) tiếp xúc với mặt phẳng ( α ) nên khoảng cách từ tâm I của mặt cầu tới mặt phằng phải bằng R, nên có :

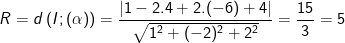
⇒ Phương trình mặt cầu tâm I ( 1 ; 4 ; – 6 ) nửa đường kính R = 5 là :
( x – 1 ) 2 + ( y – 4 ) 2 + ( z + 6 ) 2 = 25

Như vậy, từ việc tính khoảng cách từ điểm tới mặt phẳng trong không gian tọa độ, các em cũng sẽ dễ dàng tính được khoảng cách giữa hai mặt phẳng song song trong Oxyz qua việc vận dụng công thức tính khoảng cách từ điểm đến mặt phẳng.

Xem thêm : Số Nghiệm Thực Của Phương Trình Là Gì, Nghiệm Thực Của Phương Trình Là Gì Vậy
Các em hoàn toàn có thể tham thêm bài viết các dạng toán về phương trình mặt phẳng trong Oxyz để hoàn toàn có thể chớp lấy một cách tổng quát nhất về các giải pháp giải toán mặt phẳng, chúc các em học tốt .

Xem thêm bài viết thuộc chuyên mục: Cách tính

Điều hướng bài viết

Source: http://139.180.218.5
Category: tản mạn