Lý thuyết về định nghĩa và tính chất đường trung bình của tam giác

Lý thuyết về định nghĩa và tính chất đường trung bình của tam giác

Có rất nhiều đường đặc biệt trong tam giác và các dạng bài tập liên quan cũng khá đa dạng. Một trong những phần lý thuyết rất quan trọng phải kể đến là chuyên đề đường trung bình của tam giác. Mời các bạn cùng theo dõi bài viết dưới đây!

I. Định nghĩa

Đường trung bình của tam giác được hiểu là đoạn thẳng nối hai trung điểm bất kể của một tam giác, chính thế cho nên một tam giác sẽ có ba đường trung bình. Đường trung bình tạo ra những cặp cạnh có tỷ suất với nhau và song song với cạnh còn lại. Trong trường hợp nếu là tam giác đặc biệt quan trọng như tam giác đều hay tam giác cân, thì đường trung bình hoàn toàn có thể bằng nửa cạnh thứ 3.

Mới nhất:

II. Tính chất đường trung bình tam giác

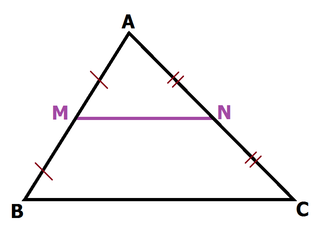
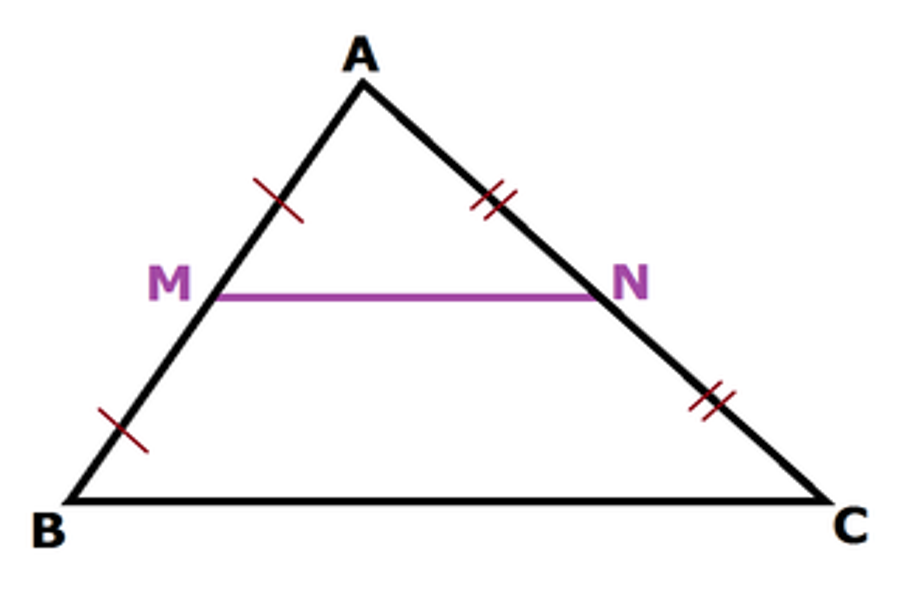
Cho tam giác ABC, cho M, N lần lượt là trung điểm của AB, AC. Vậy MN được gọi là đường trung bình của tam giác ABC. Tính chất của đường MN như sau :

• MN // BC
• \ ( \ dfrac { AM } { AB } = \ dfrac { AN } { AC } \ )
• \ ( \ Delta AMN \ đồng \ dạng \ \ Delta ABC \ )

Xem thêm: Bài tập đường trung bình tam giác

III. Các định lý

Định lý 1: Đường thẳng đi qua trung điểm của một cạnh của tam giác và song song với cạnh thứ hai thì sẽ đi qua trung điểm của cạnh thứ ba.

Cho tam giác ABC có M là trung điểm cạnh AB. Đường thẳng đi qua M song song với cạnh BC và cắt cạnh AC tại điểm N. Chứng minh \ ( { \ displaystyle NA = NC }. \ )

Chứng minh:

Từ M vẽ tia song song với AC, cắt BC tại F. Tứ giác MNCF là hình thang do có hai cạnh MN / / FC. Hình thang MNCF có hai cạnh bên song song nhau nên hai cạnh bên đó bằng nhau ( đặc thù ) : \ ( { \ displaystyle MF = NC } ( 1 ) \ ) Xét hai tam giác BMF và MAN, có : \ ( { \ displaystyle { \ widehat { \ rm { MBF } } } = { \ widehat { \ rm { AMN } } } } \ ) ( hai góc đồng vị ), \ ( { \ displaystyle BM = MA } \ ) và \ ( { \ displaystyle { \ widehat { \ rm { BMF } } } = { \ widehat { \ rm { MAN } } } } \ ) ( hai góc đồng vị ). Suy ra \ ( { \ displaystyle \ triangle BMF = \ triangle MAN } \ ) ( g. c. g ), từ đó suy ra \ ( { \ displaystyle MF = AN } \ ) ( 2 ) Từ ( 1 ) và ( 2 ) suy ra \ ( { \ displaystyle NA = NC } \ ). ( Đpcm )

Định lý 2: Đường trung bình của tam giác thì song song với cạnh thứ ba và dài bằng nửa cạnh ấy

Cho tam giác ABC có M là trung điểm cạnh AB và N là trung điểm cạnh AC \ ( ( { \ displaystyle MA = MB } \ và \ { \ displaystyle NA = NC } \ ) ). Chứng minh : \ ( { \ displaystyle { \ overline { MN } } \ parallel { \ overline { BC } } } và { \ displaystyle MN = { \ frac { 1 } { 2 } } BC }. \ )

Chứng minh:

Kéo dài đoạn MN về phía N một đoạn NF có độ dài bằng MN. Nhận thấy : \ ( { \ displaystyle \ triangle ANM = \ triangle ABC } \ ) ( c. g. c )

suy ra \({\displaystyle {\widehat {\rm {MAN}}}={\widehat {\rm {NCF}}}}\). Hai góc này ở vị trí so le trong lại bằng nhau nên \( {\displaystyle {\overline {CF}}\parallel {\overline {MA}}} \ hay \ {\displaystyle {\overline {CF}}\parallel {\overline {BA}}}.\) Mặt khác vì hai tam giác này bằng nhau nên \({\displaystyle CF=MA}\), suy ra\( {\displaystyle CF=MB}\) (vì \({\displaystyle MA=MB}\)). Tứ giác BMFC có hai cạnh đối BM và FC vừa song song, vừa bằng nhau nên BMFC là hình bình hành, suy ra \({\displaystyle {\overline {MF}}\parallel {\overline {BC}}} \ hay \ {\displaystyle {\overline {MN}}\parallel {\overline {BC}}}. \)Mặt khác, \({\displaystyle MN=NF={\dfrac {1}{2}}MF}, \ mà \ {\displaystyle MF=BC}\) (tính chất hình bình hành), nên \({\displaystyle MN={\frac {1}{2}}BC}\) (ĐPCM)

Với những lý thuyết bổ ích trên hy vọng các bạn đã hiểu được cách giải bài tập về dạng này. Nếu còn thắc mắc xin vui lòng để lại dưới mục bình luận. Chúc các bạn đạt điểm cao!

Source: http://139.180.218.5
Category: tản mạn