Chứng Minh Công Thức Tính Diện Tích Hình Chữ Nhật, Cách Tính Diện Tích Hình Chữ Nhật Như Thế Nào

Công thức tính chu vi, diện tích quy hoạnh hình chữ nhật là những kỹ năng và kiến thức cơ bản có tính ứng dụng cao mà tất cả chúng ta được học ngay từ bậc tiểu học. Ở bài viết dưới đây, lingocard.vn sẽ cùng những bạn điểm lại 1 số ít kỹ năng và kiến thức cần nhớ về hình chữ nhật và những công thức tính chu vi hình chữ nhật, công thức tính diện tích quy hoạnh hình chữ nhật .

1. Hình chữ nhật là gì? Cáctính chất của hình chữ nhật

Theo định nghĩa, chúng ta có thể hiểu hình chữ nhật là một đa giác có 4 góc vuông,trong đó có hai cạnh đối song song vàbằng nhau, cạnh ngắn hơn gọi là chiều rộng, cạnh dài hơn gọi là chiều dài.

Đang xem : Chứng minh công thức tính diện tích quy hoạnh hình chữ nhật

Hình chữ nhật có rất nhiều tính chất và ứng dụng. Nó có thể được coi là trường hợp đặc biệt của hình bình hành và hình thang cân. Khi cắt tách hình chữ nhật theo đường chéo, chúng ta sẽ có được hai tam giác vuông bằng nhau.

Để hoàn toàn có thể nhớ những đặc thù của hình chữ nhật, bạn hãy cùng tôi chứng tỏ nhé
Khi bạn có hình chữ nhật ABCD có chiều dài AB, chiều rộng BC, hai đường chéo lần lượt là AC và BD .

Khi đó, xét hai tam giác ADC và BCD ta có
Cạnh DC trùng nhau
AD = BC ( Do cùng là chiều rộng của hình chữ nhật )
Góc D bằng với góc C ( do cùng là góc vuông )
Như vậy tam giác ADC và tam giác BDC bằng nhau
Suy ra AC = BD
Gọi O là điểm giao nhau của AC và BD
Hình chữ nhật đồng thời là hình bình hành do có hai cặp cạnh song song. Vì vậy, ta hoàn toàn có thể vận dụng đặc thù của hình bình hành để suy ra O là trung điểm của cả hai cạnh AC và BD

Như vậy, từ những chứng minh trên ta có định lý hình chữ nhật có hai đường chéo bằng nhau và cắt nhau tại trung điểm của mỗi đường.

Cắt hình chữ nhật theo một đường chéo, tất cả chúng ta sẽ có hai tam giác vuông bằng nhau. Khi đó, ta sẽ nhìn rõ được đường trung tuyến ứng với cạnh huyền của mỗi tam giác vuông này có độ dài bằng nửa cạnh huyền đó .
Bạn hoàn toàn có thể tự chứng tỏ theo như cách làm của tôi để hoàn toàn có thể thuận tiện nhớ 1 số ít đặc thù của hình chữ nhật .

2.Công thức tính chu vi hình chữ nhật

Chu vi hình chữ nhật thực ra là tổng độ dài của những cạnh của hình chữ nhật. Công thức chung khi tính chu vi của những hình đa giác chính là tìm tổng của tổng thể những cạnh tạo nên đa giác đó .
Đối với hình chữ nhật, có đặc trưng chiều dài và chiều rộng bằng nhau, tất cả chúng ta hoàn toàn có thể tính chu vi hình chữ nhậtbằng cách lấy tổng chiều dài và chiều rộng nhân với hai .
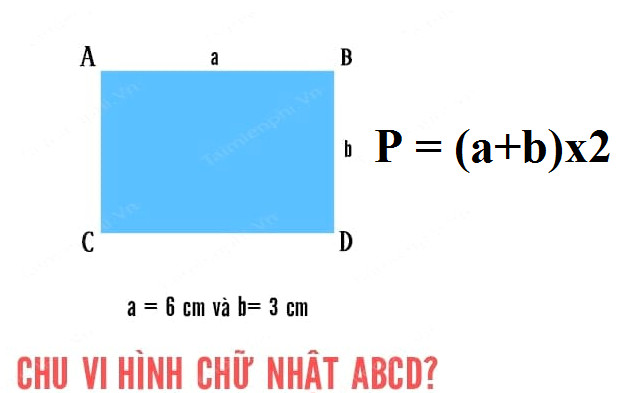
Ví dụ, ta có a, b lần lượt là chiều dài, chiều rộng của hình chữ nhật ABCD .

Khi đó, chu vi hình chữ nhật sẽ là : C = (a+b)x2 (đơn vị độ dài)

Công thức tính chu vi hình chữ nhật nói riêng và công thức tính chu vi những hình đa giác nói chung chính là tiền đề để kiến thiết xây dựng rất nhiều hệ quả, định lý được học ở những chương trình nâng cao hơn sau này .

3.Công thức tính tính diện tích hình chữ nhật

Diện tích hình chữ nhật là phần mặt phẳng số lượng giới hạn bởi bốn cạnh của hình này. Công thức tính diện tích quy hoạnh hình chữ nhật là một kỹ năng và kiến thức có tính ứng dụng cao không riêng gì trên trường học mà còn trong thực tiễn. Để tính diện tích quy hoạnh hình chữ nhật tất cả chúng ta cần tìm được độ dài 2 cạnh kề nhau của hình chữ nhật và tính theo công thức S = a. b ( trong đó a, b là độ dài 2 cạnh của hình chữ nhật )

3.1. Tính diện tính hình chữ nhật khí biết chiều dài, chiều rộng

Ví dụ, tất cả chúng ta có a, b lần lượt là chiều dài của hình chữ nhật

Khi đó, diện tích hình chữ nhật sẽ là :S = a x b ( đơn vị diện tích)

Ta hoàn toàn có thể phát biểu thành lời như sau : Diện tích của hình chữ nhật bằng tích của chiều dài và chiều rộng .
Xem thêm : Bài Giảng Số 3 : Giải He Phương Trình Bằng Cách Đặt Ẩn Phụ Lớp 9
Sau này, ở những phần kiến thức và kỹ năng nâng cao hơn, bạn sẽ hoàn toàn có thể vận dụng công thức tính diện tích quy hoạnh hình chữ nhật vào một số ít dạng bài tập hình học khoảng trống, toán dựng hình, toán quỹ tích. Đây hoàn toàn có thể được coi là công thức nền tảng làm tiền đề cho 1 số ít bài toán phức tạp ở những cấp học cao hơn .

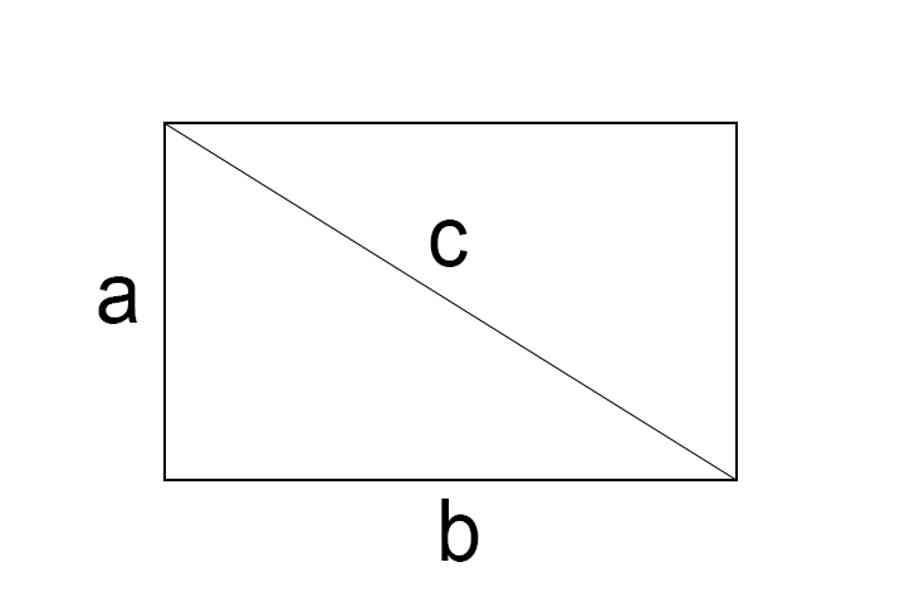
3.2. Tính diện tích hình chữ nhật khi biết độ dài 1 cạnh và đường chéo.

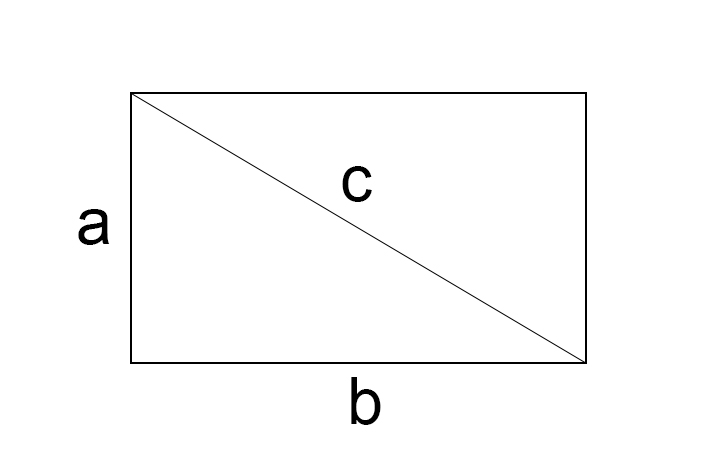
Vì hình chữ nhật có 4 góc vuông nên 2 cạnh và đường chéo sẽ tạo thành một tam giác vuông.

Áp dụng định lý pitago ta có : ( a ^ 2 + b ^ 2 = c ^ 2 )
Từ đó khi biết độ dài 1 cạnh và đường chéo ta hoàn toàn có thể tìm được độ dài cạnh còn lại và từ đó vận dụng công thức tính diện tích quy hoạnh hình chữ nhật để tính .

4.Phương pháp nhớ công thức tính chu vi, diện tích hình chữ nhật

4.1. Thường xuyên luyện tập và tìm hiểu sâu về các tính chất của hình chữ nhật

Các công thức tính chu vi hình chữ nhật, công thức tính diện tích quy hoạnh hình chữ nhật tương đối dễ nhớ và không gây quá nhiều khó khăn vất vả cho người học. Tuy nhiên, bạn cần phải nắm rõ được những đặc thù của hình để hoàn toàn có thể nhớ công thức một cách thuận tiện hơn .
Khi nhắc đến hình chữ nhật, bạn cần nắm được hình chữ nhật có hai cặp cạnh song song và bằng nhau. Khi vận dụng định nghĩa chu vi là một đường bao quanh diện tích quy hoạnh, bạn sẽ thuận tiện tự kiến thiết xây dựng được công thức tính mà không cần phải thuộc vẹt
Đối với công thức tính diện tích quy hoạnh hình chữ nhật, bạn cần phải liên tục làm bài tập, và phân biệt rõ đâu là chu vi, đâu là diện tích quy hoạnh để tránh thực trạng nhầm lẫn công thức tính. Sau một thời hạn rèn luyện, kiến thức và kỹ năng này sẽ tự động hóa được “ ghim ” vào bộ nhớ trong của bạn .

4.2. Học công thức tính chu vi, diện tích hình chữ nhật bằng thơ

Học toán bằng thơ không phải điều gì quá lạ lẫm với những bạn học viên. Khi những công thức toán khô khan được chuyển thể thành thơ, có vần điệu, những bạn sẽ rất thuận tiện ghi nhớ. Ngay từ khi mở màn đi học những năm đầu tiểu học, chắc rằng tất cả chúng ta đều đã được nghe một số ít bài toán bằng thơ, thậm chí còn cả cách giải của nó. Những bài toán đó, sau rất nhiều năm, vẫn nằm trong bộ nhớ của tất cả chúng ta, chứng tỏ, cách học toán bằng thơ là vô cùng hiệu suất cao .
Nếu bạn là giáo viên hoặc cha mẹ học viên, hoàn toàn có thể giúp con em của mình sưu tầm 1 số ít mẩu thơ vui về công thức tính chu vi hình chữ nhật, diện tích quy hoạnh hình chữ nhật trên mạng hoặc tự sáng tác để giúp học viên hoàn toàn có thể khắc ghi bài học kinh nghiệm một cách thuận tiện nhất. Tôi vẫn còn nhớ câu thơ về hình chu vi, diện tích quy hoạnh hình chữ nhật của giáo viên thời tiểu học

Diện tích chữ nhật tính sao

Dài nhân với rộng ra liền khó chi

Chu vi chữ nhật cần gì

Chiều dài cộng rộng ta thì nhân hai

Những vần thơ kiểu như trên, sẽ giúp cho học viên giảm bớt stress trong quy trình học toán đồng thời giúp những em trở nên yêu dấu môn học này hơn .

5. Bài tập thực hành về công thức tính chu vi, diện tích hình chữ nhật

Tôi xin phân phối một vài bài tập để những bạn hoàn toàn có thể vận dụng ghi nhớ những công thức này

Bài tập 1: Có một tấm bìa cứng hình chữ nhật có chu vi 100 cm. Nêu giảm chiều dài đi 15 cm và giảm chiều rộng đi 7cm thì chúng ta sẽ có chữ nhật. Xác định diện tích của tấm bìa cứng đó?

Các bạn hoàn toàn có thể tìm hiểu thêm đáp án như sau :
Tấm bìa cứng có chiều dài hơn chiều rộng là : 15 – 7 = 8 ( cm )
Nửa chu vi của hình chữ nhật là : 100 / 2 = 50 ( cm )
Chiều rộng hình chữ nhật là : ( 50 – 8 ) / 2 = 21 ( cm )
Chiều dài hình chữ nhật là : 21 + 7 = 28 ( cm )
Diện tích hình chữ nhật là : 21 x 28 = 588 ( cm vuông )

Bài tập 2: Cho một hình chữ nhật có chiều rộng bằng 24 và chu vi gấp 3 lần chiều dài. Tính chu vi hình chữ nhật, diện tích của hình chữ nhật đó

Đáp án :
Theo đầu bài, ta hoàn toàn có thể suy ra, chiều dài của hình chữ nhật gấp đôi chiều rộng
Khi đó, ta có chiều dài hình chữ nhật là : 24 x 2 = 48 ( cm )
Chu vi hình chữ nhật là : ( 24 + 48 ) X 2 = 144 ( cm )
Diện tích hình chữ nhật là : 24 x 48 = 1152 ( cm vuông )
Thông qua một số ít bài tập được cung ứng phía trên, những bạn đã hoàn toàn có thể có cái nhìn trực quan hơn về công thức tính diện tích quy hoạnh của những hình. Các bạn hoàn toàn có thể khám phá những dạng bài tập trên mạng và hoàn toàn có thể tìm hiểu và khám phá sâu hơn về công thức tính chu vi, công thức tính diện tích quy hoạnh và những ứng dụng tương quan .

Nhìn chung, môn toán đòi hỏi chúng ta phải không ngừng vận động đầu óc, phát triển tư duy. Các công thức tính chu vi, diện tích đa giác nói chung và hình chữ nhật nói riêng rất đơn giản, nhưng khi làm bài tập, các bạn cần phải nhìn ra được mấu chốt của vấn đề thì mới có thể áp dụng tốt được.Hiện nay, nhiều bạn học sinh có xu hướng rất sợ học toán, do phải đối mặt với các công thức và những bài toán hóc búa. Đừng vội nản lòng, mà hãy cố gắng nhiều hơn nữa, chắc chắn bạn sẽ thành công.

Xem thêm : tiểu luận tính độc lập tương đối của ý thức xã hội
Bài viết trên đây là những kỹ năng và kiến thức sơ lược công thức tính chu vi hình chữ nhật, công thức tính diện tích quy hoạnh của hình chữ nhật và một số ít kỹ năng và kiến thức tương quan. Hy vọng rằng sẽ giúp ích cho những bạn học viên đang có nhu yếu ôn luyện và những giáo viên, cha mẹ muốn tìm hiểu thêm kiến thức và kỹ năng để giảng dạy cho học viên .

Xem thêm bài viết thuộc chuyên mục: Diện tích

Điều hướng bài viết

Source: http://139.180.218.5
Category: tản mạn