Nội dung chính [ẩn đi]
- 1 Định nghĩa đường trung trực của đoạn thẳng là gì?
- 2 Tính chất của đường trung trực
- 3
Các dạng toán về đường trung trực của đoạn thẳng
- 3.1 Dạng 1: Chứng minh đường trung trực của một đoạn thẳng
- 3.2 Dạng 2: Chứng minh hai đoạn thẳng bằng nhau
- 3.3 Dạng 3: Bài toán về giá trị nhỏ nhất
- 3.4 Dạng 4: Xác định tâm đường tròn ngoại tiếp tam giác
- 3.5 Dạng 5: Bài toán về đường trung trực đối với tam giác cân
- 3.6 Dạng 6: Bài toán về đường trung trực đối với tam giác vuông
- 4 Một số câu hỏi về đường trung trực của đoạn thẳng
- 5 Bài tập về đường trung trực của đoạn thẳng
Định nghĩa đường trung trực của đoạn thẳng là gì?
Định nghĩa: Đường thẳng đi qua trung điểm của đoạn thẳng và vuông góc với đoạn thẳng gọi là đường trung trực của đoạn thẳng ấy.
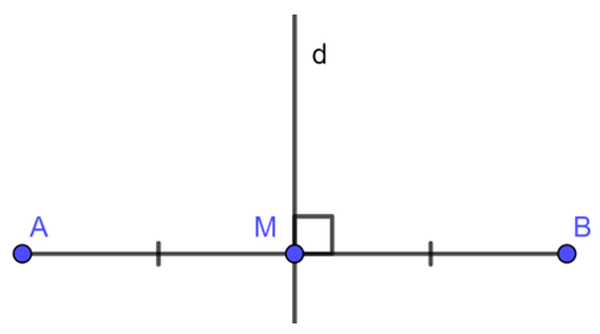
Định lý 1 : Điểm nằm trên đường trung trực của một đoạn thẳng thì cách đều hai mút của đoạn thẳng đó .GT : d là trung trực của AB, M ∈ d=> KL : MA = MBĐịnh lí 2 :Điểm cách đều hai đầu mút của một đoạn thẳng thì nằm trên đường trung trực của đoạn thẳng đóNhận xét : Tập hợp những điểm cách đều hai mút của một đoạn thẳng là đường trung trực của đoạn thẳng đó .
Tính chất của đường trung trực
– Tính chất đường trung trực một đoạn thẳng
Mọi điểm nằm trên đường trung trực của một đoạn thẳng đều cách đều hai đầu mút của đoạn thẳng ấyTrên hình vẽ trên, dd là đường trung trực của đoạn thẳng AB. Ta cũng nói : A đối xứng với B qua d .=> Nhận xét : Tập hợp những điểm cách đều hai mút của một đoạn thẳng là đường trung trực của đoạn thẳng đó .
Tính chất ba đường trung trực trong tam giác
Với tam giác thường
– Ba đường trung trực của một tam giác cùng đi qua một điểm. Điểm này cách đều ba đỉnh của tam giác đó .
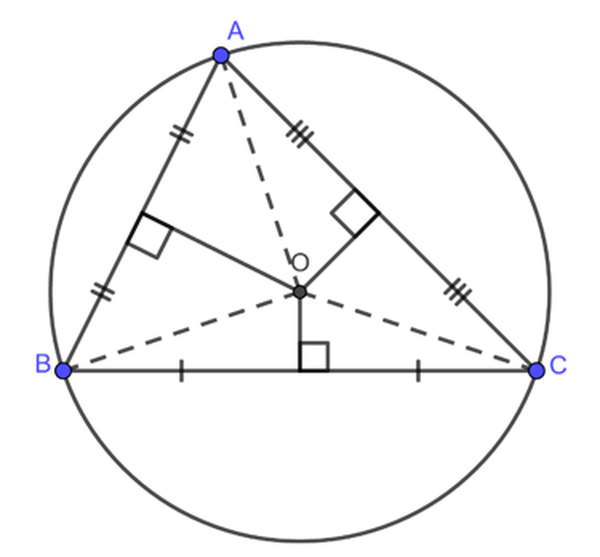
Trên hình, điểm O là giao điểm những đường trung trực của ΔABC. ΔABC .Ta có OA = OB = OC. Điểm OO là tâm đường tròn ngoại tiếp ΔABC. ΔABC .– Giao điểm của ba đường trung trực của một tam giác là tâm đường tròn ngoại tiếp tam giác đó .O là giao điểm của ba đường trung trực của tam giác ABC. Khi đó, O là tâm đường tròn ngoại tiếp tam giác ABC
Với tam giác cân
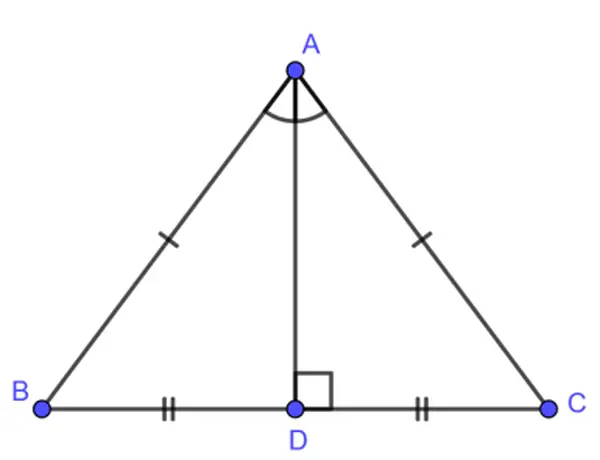
Trong tam giác cân, đường trung trực ứng với cạnh đáy đồng thời là đường phân giác, đường trung tuyến và đường cao cùng xuất phát từ đỉnh đối lập với cạnh đó .
Với tam giác vuông
Trong tam giác vuông, giao điểm của ba đường trung trực chính là trung điểm của cạnh huyền .
Các dạng toán về đường trung trực của đoạn thẳng
Dạng 1: Chứng minh đường trung trực của một đoạn thẳng
Dạng 1 : Toán chứng tỏ đường trung trực của một đoạn thẳngPhương pháp giải :Chứng minh d là đường trung trực của đoạn thẳng AB, ta chứng tỏ d chứa hai điểm và cách đều A và B hoặc dùng định nghĩa đường trung trực .
Dạng 2: Chứng minh hai đoạn thẳng bằng nhau
Dạng 2 : Chứng minh hai đoạn thẳng bằng nhauPhương pháp :Áp dụng định lý : “ Điểm nằm trên đường trung trực của một đoạn thẳng thì cách đều hai mút của đoạn thẳng đó. ”
Dạng 3: Bài toán về giá trị nhỏ nhất
Dạng 3 : Bài toán về giá trị nhỏ nhấtPhương pháp :Áp dụng đặc thù đường trung trực để thay độ dài một đoạn thẳng thành độ dài một đoạn thẳng khác bằng nó .Sau đó là vận dụng bất đẳng thức tam giác để tìm giá trị nhỏ nhất .
Dạng 4: Xác định tâm đường tròn ngoại tiếp tam giác
Dạng 4 : Xác định tâm đường tròn ngoại tiếp tam giácPhương pháp :Áp dụng đặc thù giao điểm 3 đường trung trực của tam giácĐịnh lý : Ba đường trung trực của một tam giác cùng đi qua một điểm. Điểm này cách đều ba đỉnh của tam giác đó .
Dạng 5: Bài toán về đường trung trực đối với tam giác cân
Dạng 5 : Bài toán tương quan đến đường trung trực so với tam giác cânPhương pháp :Cần nhớ trong tam giác cân, đường trung trực của cạnh đáy đồng thời là đường trung tuyến, đường phân giác ứng với cạnh đáy này .
Dạng 6: Bài toán về đường trung trực đối với tam giác vuông
Dạng 6 : Bài toán tương quan đến đường trung trực so với tam giác vuôngPhương pháp :Cần ghi nhớ và vận dụng : Trong tam giác vuông, giao điểm những đường trung trực là trung điểm cạnh huyền .Bạn hoàn toàn có thể tìm hiểu thêm bài học kinh nghiệm về Đường trung trực tại đây :
Một số câu hỏi về đường trung trực của đoạn thẳng
Mỗi đoạn thẳng có bao nhiêu đường trung trực ? Mỗi đoạn thẳng chỉ có một đường trung trực, là đường thẳng đi qua trung điểm và vuông góc với đoạn thẳng đó .Cách viết phương trình đường trung trực của đoạn thẳng ?Dựa vào định nghĩa và đặc thù của đường trung trực cộng với đặc thù của vectơ, có 2 chiêu thức viết phương trình đường trung trực của đoạn thẳng :
- Tìm vectơ pháp tuyến của đường trung trực và 1 điểm mà nó đi qua .
- Áp dụng đặc thù 1 ở trên .
Bài tập vận dụng cách 1 : tìm vectơ pháp tuyếnCho A ( 1 ; – 4 ) và B ( 3 ; 2 ), viết pt tổng quát đường trung trực của đoạn AB .Giải :Vectơ AB = ( 3 – 1 ; 2 – ( – 4 ) ) = ( 2 ; 6 ) = 2 ( 1 ; 3 )=> Vectơ pháp tuyến của đường trung trực của đoạn AB là : Vectơ n = ( 1 ; 3 )Gọi I ( x ; y ) là trung điểm của ABx = ( 1 + 3 ) / 2 = 2Và y = ( – 4 + 2 ) / 2 = – 1=> I ( 2 ; – 1 )Phương trình tổng quát đường trung trực của đoạn AB :a ( x – x0 ) + b ( y – y0 ) = 0
<=> x – 2 + 3(y + 1 ) = 0
=> x + 3 y + 1 = 0
Bài tập về đường trung trực của đoạn thẳng
Bài 44 ( trang 76 SGK Toán 7 tập 2 ) : Gọi M là điểm nằm trên đường trung trực của đoạn thẳng AB, cho đoạn thẳng MA có độ dài 5 cm. Hỏi độ dài MB bằng bao nhiêu ?Bài giải :
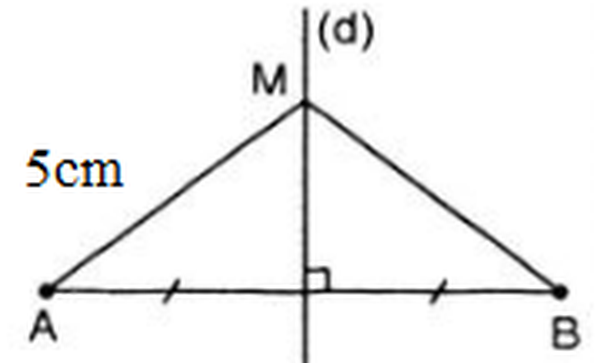
Điểm M thuộc đường trung trực của AB=> MA = MB ( định lí thuận )Vì MA = 5 cm nên MB = 5 cmKiến thức vận dụng : Dựa vào định lí về đặc thù của những điểm thuộc đường trung trực ( định lý thuận ) : Điểm nằm trên đường trung trực của một đoạn thẳng thì cách đều hai mút của đoạn thẳng đó .Bài 45 ( trang 76 SGK Toán 7 tập 2 ) : Chứng minh đường thẳng PQ được vẽ như trong hình đúng là đường trung trực của đoạn thẳng MN .
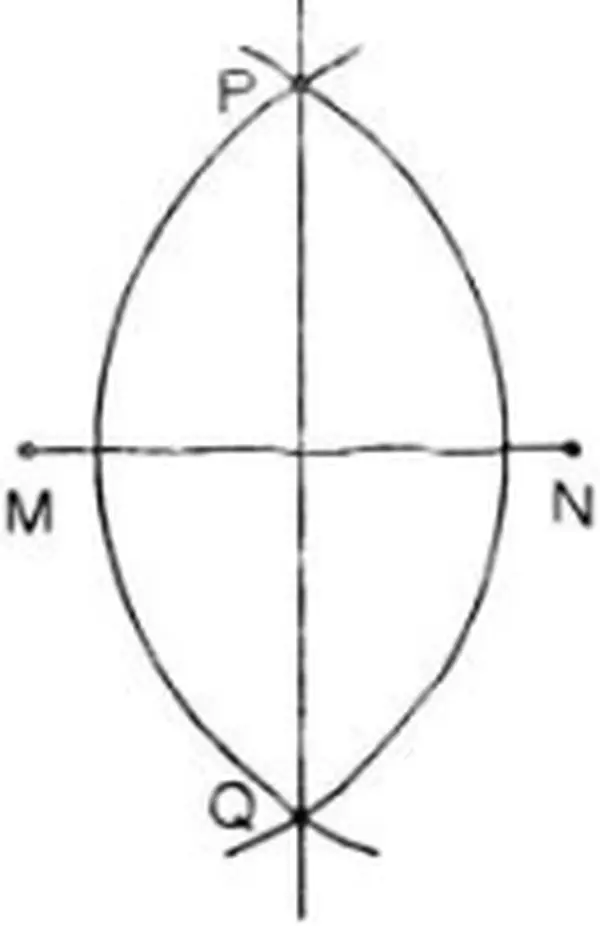
Lời giải :Ta có : Hai cung tròn tâm M và N có nửa đường kính bằng nhau và cắt nhau tại P., Q. .Nên MP = NP và MQ = NQ=> P. ; Q. cách đều hai mút M, N của đoạn thẳng MN
nên theo định lí 2 : P; Q thuộc đường trung trực của MN
hay đường thẳng qua P., Q. là đường trung trực của MN .Vậy PQ là đường trung trực của MN .Bài 46 ( trang 76 SGK Toán 7 tập 2 ) : Cho ba tam giác cân ABC, DBC, EBC có chung đáy BC. Chứng minh ba điểm A, D, E thẳng hàng .
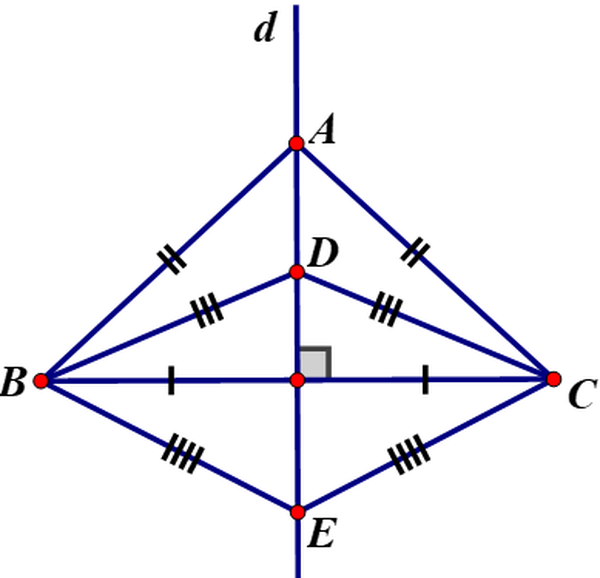
Lời giải :Vì ΔABC cân tại A ⇒ AB = AC=> A thuộc đường trung trực của BC .Vì ΔDBC cân tại D ⇒ DB = DC=> D thuộc đường trung trực của BCVì ΔEBC cân tại E ⇒ EB = EC=> E thuộc đường trung trực của BCDo đó A, D, E cùng thuộc đường trung trực của BCVậy A, D, E thẳng hàngBài 47 ( trang 76 SGK Toán 7 tập 2 ) : Cho hai điểm M, N nằm trên đường trung trực của đoạn thẳng AB. Chứng minh ΔAMN = Δ BMN .Bài giải :
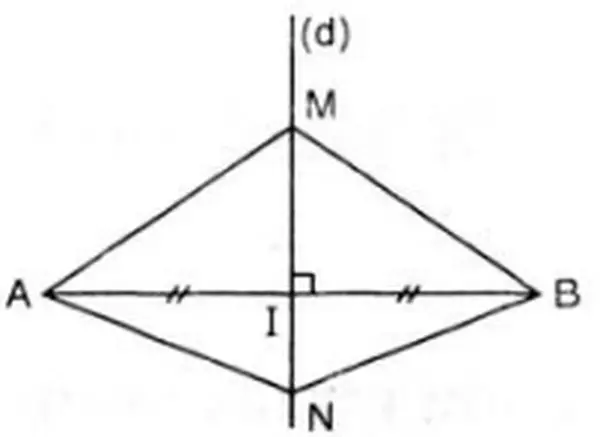
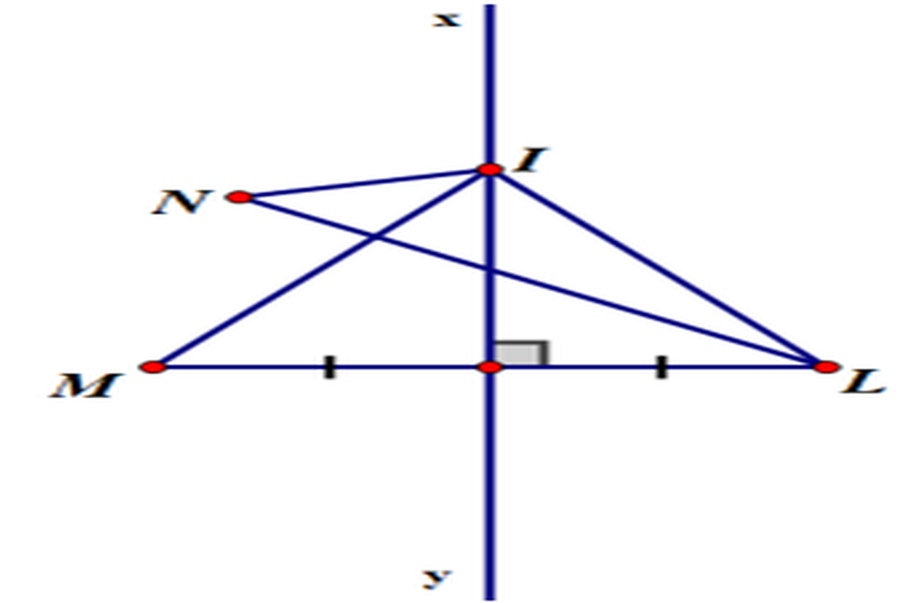
Vì M thuộc đường trung trực của AB=> MA = MB ( định lý thuận về đặc thù của những điểm thuộc đường trung trực )N thuộc đường trung trực của AB=> NA = NB ( định lý thuận về đặc thù của những điểm thuộc đường trung trực )Do đó ΔAMN và ΔBMN có :AM = BM ( cmt )MN chungAN = BN ( cmt )⇒ ΔAMN = ΔBMN ( c. c. c )Bài 48 ( trang 77 SGK Toán 7 tập 2 ) : Hai điểm M và N cùng nằm trên 50% mặt phẳng bờ là đường thẳng xy. Lấy điểm L đối xứng với M qua xy. Gọi I là một điểm của xy. Hãy so sánh IM + IN với LN .Bài giải :Vì L và M đối xứng qua đường thẳng xy nên xy là đường thẳng đi qua trung điểm và vuông góc với ML .Nên đường thẳng xy là trung trực của ML .I ∈ xy => IM = IL ( theo định lý 1 ) .Nên IM + IN = IL + IN– TH1 : Nếu I, L, N thẳng hàng=> IL + IN = LN ( vì N và L nằm khác phía so với đường thẳng xy và I nằm trên xy ) .=> IM + IN = LN
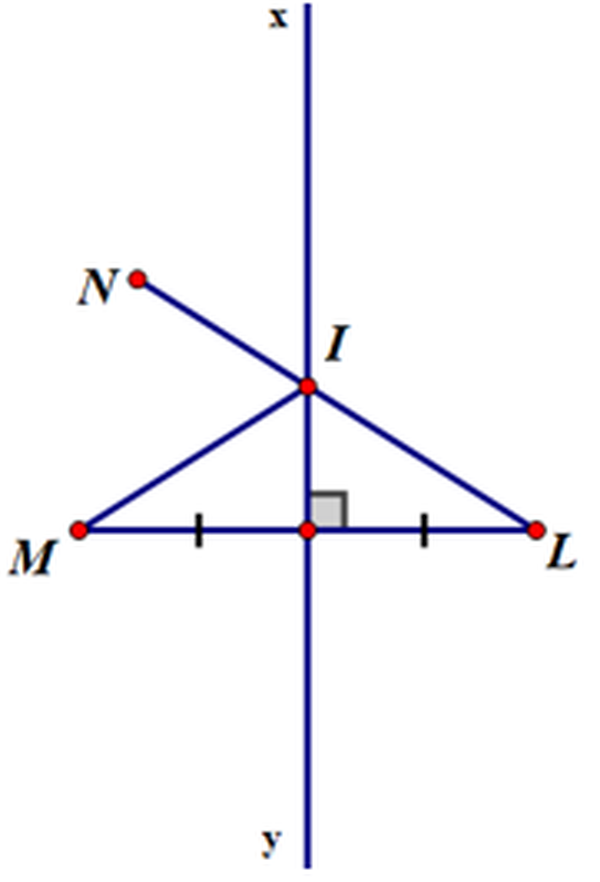
TH2 : Nếu I không là giao điểm của LN và xy thì ba điểm I, L, N không thẳng hàngÁp dụng bất đẳng thức tam giác vào Δ INL ta được : IL + IN > LNmà IM = IL ( cmt )=> IL + IN > LN ( bất đẳng thức tam giác )=> IM + IN > LN
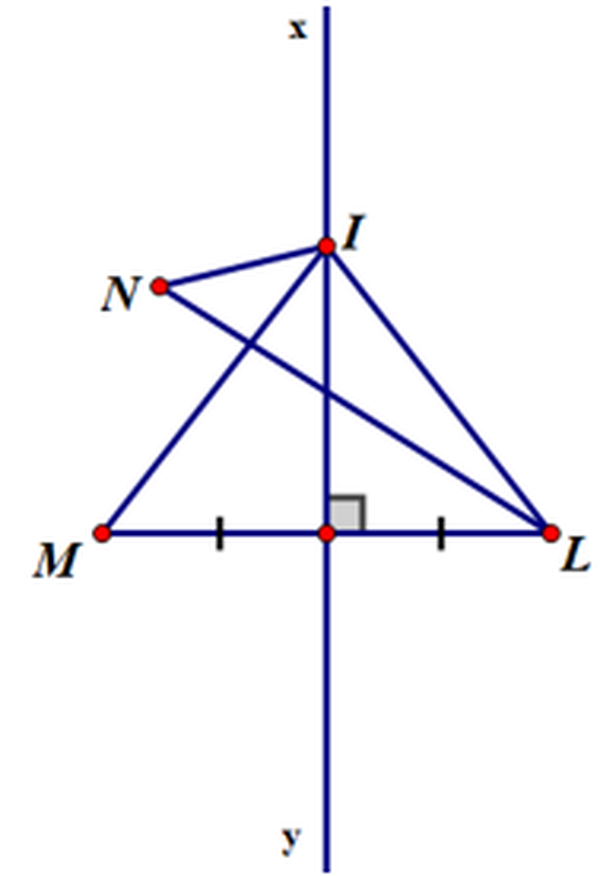
Vậy với mọi vị trí của I trên xy thì IM + IN ≥ LNBài 49 ( trang 77 SGK Toán 7 tập 2 ) : Hai xí nghiệp sản xuất được thiết kế xây dựng bên bờ một con sông tại hai khu vực A và B ( h. 44 ). Hãy tìm trên bờ sông một khu vực C để kiến thiết xây dựng một trạm bơm đưa nước về cho hai nhà máy sản xuất sao cho độ dài đường ống dẫn nước là ngắn nhất ?
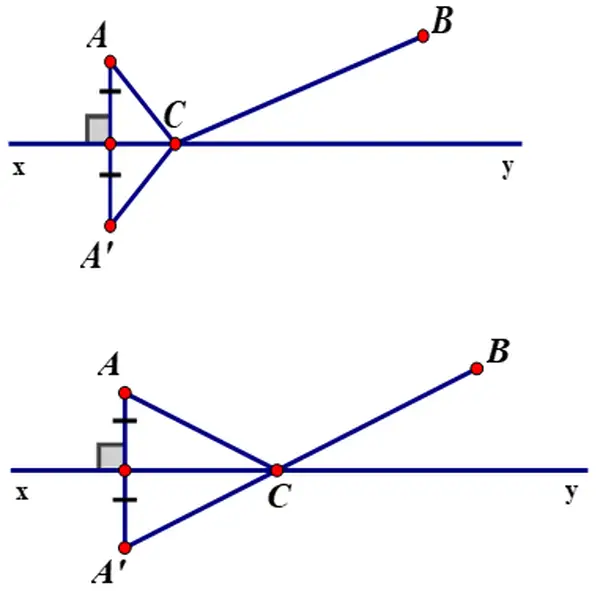
Lời giải :Gọi đường thẳng xy là bờ sông cần xây trạm bơm .=> Bài toán đưa về : Hai điểm A, B cố định và thắt chặt cùng nằm trên nửa mặt phẳng bờ là đường thẳng xy. Tìm vị trí điểm C nằm trên đường xy sao cho CA + CB nhỏ nhất .Gọi A ’ là điểm đối xứng của A qua đường thẳng xy .Theo như chứng tỏ ở bài 48 ta có : CA + CB = CA ’ + CB ≥ A’B ( A’B cố định và thắt chặt ) .=> CA + CB đạt ngắn nhất bằng A’B .Dấu “ = ” xảy ra khi CA ’ + CB = A’B, tức là A ’ ; B ; C thẳng hàng hay C là giao điểm của A’B và xy .Vậy điểm đặt trạm bơm là giao điểm của đường thẳng xy với đường thẳng A’B, trong đó A ’ là điểm đối xứng với A qua xyBài 51 ( trang 77 SGK Toán 7 tập 2 ) : Cho đường thẳng d và điểm P. không nằm trên d. Hình 46 minh họa cho cách dựng đường thẳng đi qua điểm P. vuông góc với đường thẳng d bằng thước và compa như sau 
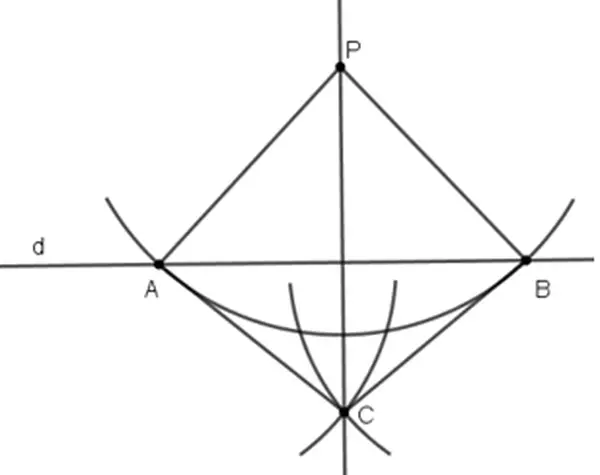
- a ) Ta có : PA = PB ( A ; B nằm trên cung tròn tâm P. ) nên P. nằm trên đường trung trực của AB .
CA = CB ( C nằm trên 2 cung tròn tâm A, B nửa đường kính bằng nhau ) nên C nằm trên đường trung trực của AB .Vậy CP là đường trung trực của AB, suy ra PC ⊥ d .
- b ) Một cách vẽ khác
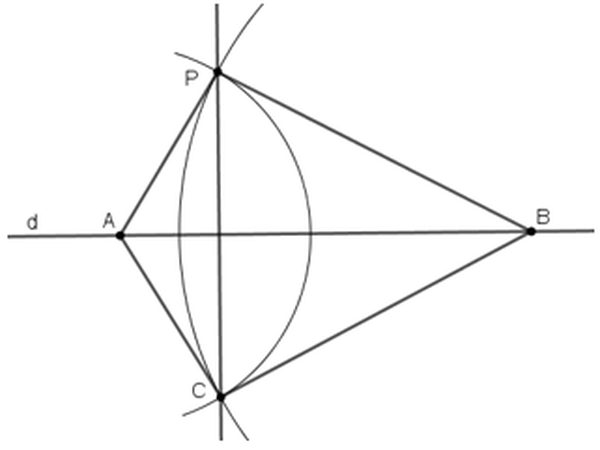
– Lấy hai điểm A, B bất kỳ trên d .– Vẽ cung tròn tâm A bán kính AP, cung tròn tâm B nửa đường kính BP. Hai cung tròn cắt nhau tại C ( C khác P. ) .– Vẽ đường thẳng PC. Khi đó PC là đường đi qua P. và vuông góc với dChứng minh :– Theo định lí 2 :PA = CA ( P., C cùng thuộc cung tròn tâm A bán kính PA )=> A thuộc đường trung trực của PC .PB = CB ( P., C cùng thuộc cung tròn tâm B nửa đường kính PB )=> B thuộc đường trung trực của PC .
=> AB là đường trung trực của PC
=> PC ⏊ AB hay PC ⏊ d .Hy vọng với phần kỹ năng và kiến thức cần nhớ cũng như những dạng toán quen thuộc về đường trung trực đã san sẻ ở trên bạn sẽ thuận tiện hơn trong việc giải những bài tập tương quan. Định lí và định nghĩa về đường trung trực là hai phần quan trọng nhất buộc bạn phải thuộc lòng để vận dụng nhanh nhất vào giải toán. Hình học luôn có sự mê hoặc khi càng lên bậc cao hơn, đường trung trực chính là bài học kinh nghiệm nền tảng cho bạn sau này .
Source: http://139.180.218.5
Category: tản mạn