Mời những bạn cùng tìm hiểu và khám phá khái niệm hình nón cụt và cách tính thể tích hình nón cụt cùng với ví dụ đơn cử mà bài viết san sẻ dưới đây .

Khái niệm hình nón cụt

Hình nón cụt được tạo ra từ hình nón như sau: cho tam giác AOC vuông ở O. Khi quay tam giác vuông này một vòng quanh cạnh OA ta sẽ được một hình nón. Cạnh OC quét đáy tạo thành một hình tròn tâm O bán kính OC. Trong khi đó, cạnh AC quét tạo thành mặt xung quanh của hình nón và cạnh AC được gọi là đường sinh của hình nón.

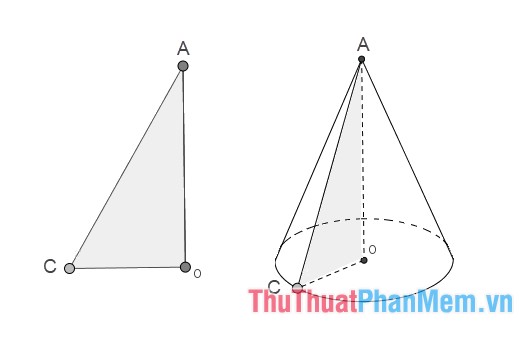
Từ hình nón đã được tạo thành, ta dùng một mặt phẳng song song đáy cắt qua hình nón, ta được một hình nón cụt .

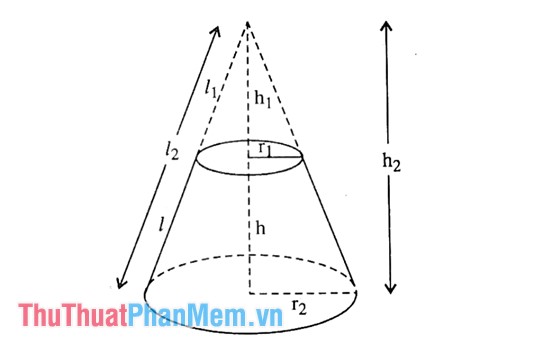
Như vậy, hình nón cụt là hình có 2 đáy là hai hình tròn trụ có nửa đường kính to nhỏ khác nhau nằm trên hai mặt phẳng song song có đường nối tâm là trục đối xứng .

Công thức tính thể tích hình nón cụt

Giả sử ta có hình nón cụt với r1 và r2 lần lượt là bán kính hai đáy của hình nón cụt, h là chiều cao và l là độ dài đường sinh.

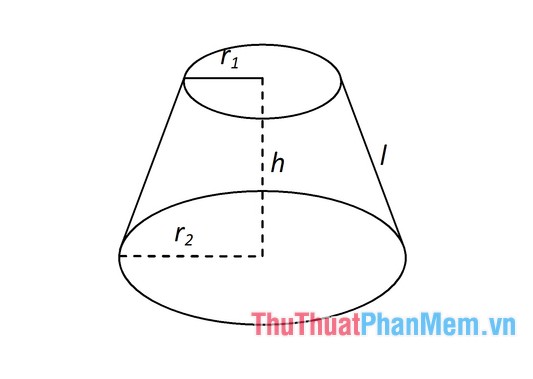
Ta có công thức tính thể tính hình nón cụt :
\ [ V = \ frac { 1 } { 3 } \ pi \ left ( { { r_1 } ^ 2 + { r_2 } ^ 2 + { r_1 } { r_2 } } \ right ) h \ ]
Trong đó :

• V là thể tích hình nón cụt.
• r1, r2: hai bán kính của hai đáy hình nón cụt.
• h : Chiều cao nối giữa hai đáy của hình nón cụt.
• π: số Pi (3.14159265).

Cách tính thể tích hình nón cụt

1. Để tính thể tích hình nón cụt các bạn cần dựa vào các dữ liệu đề bài cho sau đó các bạn tính r1, r2, h. Nếu các đề bài cho sẵn r1, r2, h thì các bạn thực hiện luôn bước 2.

2. Sau đó vận dụng công thức tính thể tích hình nón cụt :
\ [ V = \ frac { 1 } { 3 } \ pi \ left ( { { r_1 } ^ 2 + { r_2 } ^ 2 + { r_1 } { r_2 } } \ right ) h \ ]
Và tính hiệu quả của thể tích .

Ví dụ

Cho hình nón cụt có đường kính hai dưới mặt đáy lần lượt là 12 cm và 16 cm. Chiều cao nối giữa hai mặt đáy dài 7 cm. Tính thể tích hình nón cụt .
Giải
Đường kính hai mặt dưới lần lượt là 12 cm và 18 cm .
Vậy nửa đường kính đáy \ ( { r_1 } = \ frac { { 12 } } { 2 } = 6 cm ; { r_2 } = \ frac { { 18 } } { 2 } = 9 cm ; h = 7 cm \ )

\[V = \frac{1}{3}\pi \left( {{r_1}^2 + {r_2}^2 + {r_1}{r_2}} \right)h\]

\ ( \ Rightarrow V = \ frac { 1 } { 3 } \ pi. \ left ( { { 6 ^ 2 } + { 9 ^ 2 } + 6.9 } \ right ). 7 = \ frac { 1 } { 3 } \ pi. \ left ( { 36 + 91 + 57 } \ right ). 7 = 1253,5 c { m ^ 3 } \ )
Vậy thể tích hình nón cụt giao động \ ( 1253,5 c { m ^ 3 } \ )
Trên đây bài viết đã san sẻ đến những bạn khái niệm hình nón cụt, công thức tính thể tích hình nón cụt và cách tính thể tích hình nón cụt với ví dụ đơn cử. Hi vọng những bạn sẽ hiểu và vận dụng tính thể tích hình nón cụt chuẩn nhất. Chúc những bạn thành công xuất sắc !

Source: http://139.180.218.5
Category: tản mạn