Nội dung chính [ẩn đi]
Bài tập áp dụng công thức, thể tích mặt trụ, hình trụ, khối trụ có đáp án chi tiết
Bài tập trắc nghiệm công thức, thể tích mặt trụ, khố trụ có đáp án chi tiết
| Bài tập 1: Một hình trụ có diện tích xung quanh bằng $4\pi {{a}^{2}}$ và bán kính đáy là a. Tính độ dài đường cao của hình trụ đó.
A. $l=2a.$ B. $l=a.$ C. $l=4a.$ D. $l=\frac{a}{2}.$ |
Lời giải chi tiết
Ta có USD { { S } _ { xq } } = 4 \ pi { { a } ^ { 2 } } = 2 \ pi Rh \ xrightarrow { { } } Rh = 2 { { a } ^ { 2 } } $ mà $ R = a \ Rightarrow { { a } ^ { 2 } } h = 2 { { a } ^ { 2 } } \ Leftrightarrow h = 2 a USD
Vậy độ dài đường sinh của hình trụ là $l=h=2a.$Chọn A.
Bạn đang đọc: Bài tập áp dụng công thức, thể tích mặt trụ, hình trụ, khối trụ có đáp án chi tiết – Tự Học 365
| Bài tập 2: Cho hình trụ có bán kính đáy bằng R, chiều cao bằng h. Biết rằng hình trụ đó có diện tích toàn phần gấp đôi diện tích xung quanh. Mệnh đề nào sau đây đúng?
A. $h=R\sqrt{2}.$ B. $h=R.$ C. $h=2R.$ D. $2h=R.$ |
Lời giải chi tiết
Diện tích xung quanh của hình tròn trụ là USD { { S } _ { xq } } = 2 \ pi Rh $
Diện tích toàn phần của hình tròn trụ là USD { { S } _ { tp } } = 2 \ pi Rh + 2 \ pi { { R } ^ { 2 } } $
Theo bài ra, ta có ${{S}_{tp}}=2{{S}_{xq}}\Leftrightarrow 2\pi Rh+2\pi {{R}^{2}}=2.2\pi Rh\Leftrightarrow 2\pi {{R}^{2}}=2\pi Rh\Leftrightarrow R=h.$Chọn B.
| Bài tập 3: Cho hình trụ có bán kính đáy bằng a, diện tích toàn phần bằng $4\pi {{a}^{2}}$. Thể tích khối trụ đã cho bằng
A. $V=2\pi {{a}^{3}}.$ B. $V=\sqrt{2}\pi {{a}^{3}}.$ C. $V=\pi {{a}^{3}}.$ D. $V=4\pi {{a}^{3}}.$ |
Lời giải chi tiết
Diện tích toàn phần của hình tròn trụ là USD { { S } _ { tp } } = 2 \ pi Rh + 2 \ pi { { R } ^ { 2 } } $
Mặt khác $ R = a, { { S } _ { tp } } = 4 \ pi { { a } ^ { 2 } } $ suy ra USD 4 \ pi { { a } ^ { 2 } } = 2 \ pi ah + 2 \ pi { { a } ^ { 2 } } \ xrightarrow [ { } ] { } h = a USD
Vậy thể tích khối trụ là $V=\pi {{R}^{2}}h=\pi .{{a}^{2}}.a=\pi {{a}^{3}}.$Chọn C.
| Bài tập 4: Cho hình trụ có khoảng cách giữa hai đáy bằng a, thế tích khối tại bằng $4\pi {{a}^{3}}.$ Diện tích toàn phần hình trụ đã cho là
A. ${{S}_{tp}}=-8\pi {{a}^{2}}.$ B. ${{S}_{tp}}=-4\pi {{a}^{2}}.$ C. ${{S}_{tp}}=2\pi {{a}^{2}}.$ D. ${{S}_{tp}}=12\pi {{a}^{2}}.$ |
Lời giải chi tiết
Khoảng cách giữa hai đáy của hình tròn trụ chính là chiều cao USD h \ xrightarrow [ { } ] { } h = a USD
Thể tích khối trụ là $ V = \ pi { { R } ^ { 2 } } h = 4 \ pi { { a } ^ { 3 } } $ mà USD h = a \ Rightarrow { { R } ^ { 2 } } = 4 { { a } ^ { 2 } } \ Leftrightarrow R = 2 a USD
Vậy diện tích toàn phần của hình trụ là ${{S}_{tp}}=2\pi Rh+2\pi {{R}^{2}}=12\pi {{a}^{2}}.$ Chọn D.
| Bài tập 5: Cho hình trụ có diện tích xung quanh bằng 4π, diện tích toàn phần bằng 12π. Thể tích khối trụ đã cho bằng
A. $V=12\pi .$ B. $V=4\pi .$ C. $V=8\pi .$ D. $V=6\pi .$ |
Lời giải chi tiết
Diện tích xung quanh của hình tròn trụ là USD { { S } _ { xq } } = 2 \ pi Rh = 4 \ pi \ xrightarrow { { } } Rh = 2 USD
Diện tích toàn phần của hình tròn trụ là USD { { S } _ { tp } } = 2 \ pi Rh + 2 \ pi { { R } ^ { 2 } } = 12 \ pi \ xrightarrow { { } } Rh + { { R } ^ { 2 } } = 6 USD
Khi đó, ta có hệ $ \ left \ { \ begin { array } { } Rh = 2 \ \ { } Rh + { { R } ^ { 2 } } = 6 \ \ \ end { array } \ right. \ Leftrightarrow \ left \ { \ begin { array } { } Rh = 2 \ \ { } { { R } ^ { 2 } } = 4 \ \ \ end { array } \ right. \ Leftrightarrow \ left \ { \ begin { array } { } R = 2 \ \ { } h = 1 \ \ \ end { array } \ right .. $
Vậy thể tích khối trụ đã cho là $V=\pi {{R}^{2}}h=\pi {{.2}^{2}}.1=4\pi .$ Chọn B.
| Bài tập 6: Cho hình trụ có diện tích toàn phần bằng 16π, thể tích khối trụ bằng 8π. Diện tích xung quanh hình trụ đã cho bằng
A. $V=12\pi .$ B. $V=4\pi .$ C. $V=8\pi .$ D. $V=6\pi .$ |
Lời giải chi tiết
Diện tích toàn phần của hình tròn trụ là USD { { S } _ { tp } } = 2 \ pi Rh + 2 \ pi { { R } ^ { 2 } } = 16 \ pi \ xrightarrow { { } } Rh + { { R } ^ { 2 } } = 8 USD
Thể tích của khối trụ là $ V = \ pi { { R } ^ { 2 } } h = 8 \ pi \ xrightarrow { { } } { { R } ^ { 2 } } h = 8 USD
Khi đó, ta có hệ $ \ left \ { \ begin { array } { } Rh + { { R } ^ { 2 } } = 8 \ \ { } { { R } ^ { 2 } } h = 8 \ \ \ end { array } \ right. \ Leftrightarrow \ left \ { \ begin { array } { } h = \ frac { 8 } { { { R } ^ { 2 } } } \ \ { } R. \ frac { 8 } { { { R } ^ { 2 } } } + { { R } ^ { 2 } } = 8 \ \ \ end { array } \ right. \ Leftrightarrow \ left \ { \ begin { array } { } h = \ frac { 8 } { { { R } ^ { 2 } } } \ \ { } { { R } ^ { 2 } } + \ frac { 8 } { R } = 8 \ \ \ end { array } \ right. \ Leftrightarrow h = R = 2. $
Vậy diện tích xung quanh của hình trụ là ${{S}_{xq}}=2\pi Rh=8\pi .$ Chọn C.
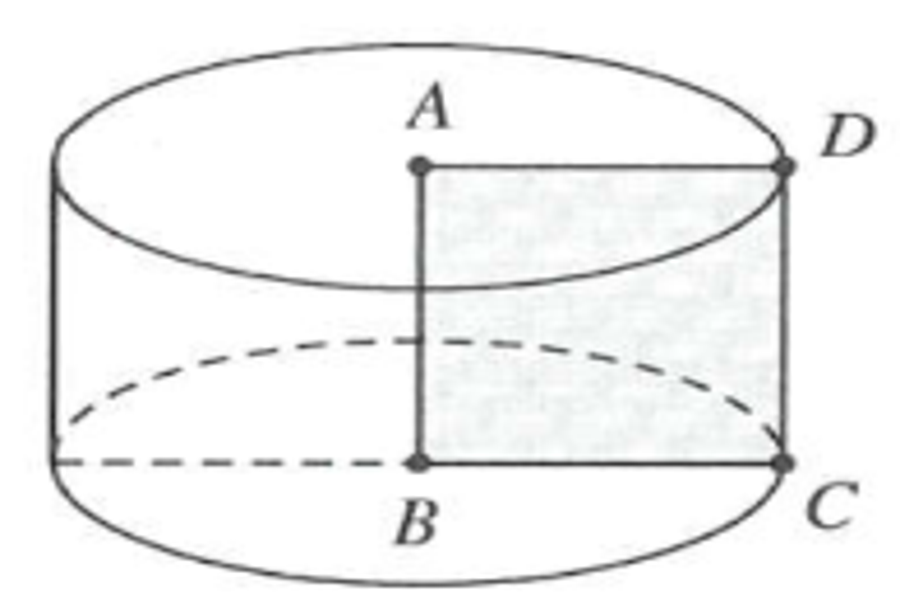
| Bài tập 7: Cho hình chữ nhật ABCD có AB = a, AD = 2a. Thể tích của khối trụ tạo thành khi quay hình chữ nhật ABCD quanh cạnh AB bằng
A. $4\pi {{a}^{3}}.$ B. $2\pi {{a}^{3}}.$ C. $8\pi {{a}^{3}}.$ D. $12\pi {{a}^{3}}.$ |
Lời giải chi tiết

Kỹ năng vẽ hình: Hình chữ nhật quay quanh cạnh nào thì cạnh đó là trục, đồng thời chính là chiều cao của hình trụ
Khi quay hình chữ nhật ABCD quanh trục AB, ta được hình tròn trụ có chiều cao USD h = AB = a, USD nửa đường kính đáy USD R = AD = 2 a USD
Vậy thể tích của khối trụ là $V=\pi {{R}^{2}}h=\pi .4{{a}^{2}}.a=4\pi {{a}^{3}}.$Chọn A.
| Bài tập 8: Hình trụ (T) được sinh ra khi quay hình chữ nhật ABCD xung quanh MN, với M, N lần lượt là trung điểm AB và CD. Biết $AC=2a\sqrt{2},\text{ }\widehat{ACB}={{45}^{0}}.$Diện tích toàn phần của hình trụ đã cho bằng
A. $4\pi {{a}^{3}}.$ B. $12\pi {{a}^{3}}.$ C. $8\pi {{a}^{3}}.$ D. $6\pi {{a}^{3}}.$ |
Lời giải chi tiết

Tam giác ABC vuông tại B, có $ \ widehat { ACB } = { { 45 } ^ { 0 } } \ Rightarrow AB = BC $
Ta có $ A { { C } ^ { 2 } } = A { { B } ^ { 2 } } + B { { C } ^ { 2 } } \ Leftrightarrow 2A { { B } ^ { 2 } } = 8 { { a } ^ { 2 } } \ Leftrightarrow AB = BC = 2 a USD
Quay hình chữ nhật ABCD quanh MN ta được hình tròn trụ có chiều cao USD h = MN = BC = 2 a, USD nửa đường kính đáy USD R = MB = \ frac { AB } { 2 } = a $
Vậy diện tích toàn phần là ${{S}_{tp}}=2\pi Rh+2\pi {{R}^{2}}=6\pi {{a}^{3}}$. Chọn D.
| Bài tập 9: Từ một tấm tôn hình chữ nhật có kích thước 50 ´ 240, người ta làm các thùng đựng nước hình trụ có chiều cao bằng 50, theo hai cách sau (xem hình vẽ minh họa):
A. $\frac{1}{2}.$ B. 1. C. 2. D. 4. |
Lời giải chi tiết
Công thức thể tích khối trụ là $ V = \ pi { { R } ^ { 2 } } h USD
- Ở cách 1, suy ra $h=50$ và $2\pi {{R}_{1}}=240\Leftrightarrow {{R}_{1}}=\frac{120}{\pi }.$ Do đó ${{V}_{1}}=\pi .{{\left( \frac{120}{\pi } \right)}^{2}}.50$ (đvtt).
- Ở cách 2, suy ra mỗi thùng có $h=50$ và $2\pi {{R}_{2}}=120\Leftrightarrow {{R}_{2}}=\frac{60}{\pi }.$
Do đó ${{V}_{2}}=2\times \left[ \pi .{{\left( \frac{60}{\pi } \right)}^{2}}.50 \right]$ (đvtt). Suy ra $\frac{{{V}_{1}}}{{{V}_{2}}}=2.$ Chọn C.
| Bài tập 10: Người ta thả một viên billiards snooker có dạng hình cầu với bán kính nhỏ hơn 4,5 cm vào một chiếc cốc hình trụ đang chứa nước thì viên billiards đó tiếp xúc với đáy cốc và tiếp xúc với mặt nước sau khi dâng (tham khảo hình vẽ bên). Biết rằng bán kính của phần trong đáy cốc bằng 5,4 cm và chiều cao của mực nước ban đầu trong cốc bằng 4,5 cm. Bán kính của viên billiards đó bằng
A. 2,7 cm. Xem thêm: Cuộc sống vốn luôn chứa đựng những muộn phiền, cũng may còn có bầu trời luôn cho ta niềm tin! B. 4,2 cm. C. 3,6 cm. D. 2,6 cm. |
Lời giải chi tiết
Thể tích của phần chứa nước bắt đầu là USD { { V } _ { 1 } } = \ pi. { { \ left ( 5,4 \ right ) } ^ { 2 } }. 4,5 = \ frac { 6561 \ pi } { 50 } \ left ( c { { m } ^ { 3 } } \ right ) USD
Gọi R là nửa đường kính của viên billiards Þ Thể tích viên billiards là USD { { V } _ { 2 } } = \ frac { 4 \ pi { { R } ^ { 3 } } } { 3 } \ left ( c { { m } ^ { 3 } } \ right ) USD
Tổng thể tích của nước và bi là $ V = \ pi. { { \ left ( 5,4 \ right ) } ^ { 2 } }. 2 \ text { R } = \ frac { 1458 \ pi R } { 25 } \ left ( c { { m } ^ { 3 } } \ right ) USD
Khi đó, ta có USD V = { { V } _ { 1 } } + { { V } _ { 2 } } \ Leftrightarrow \ frac { 1458 \ pi R } { 25 } = \ frac { 6561 \ pi } { 50 } + \ frac { 4 \ pi { { R } ^ { 3 } } } { 3 } $
Giải phương trình với điều kiện $0
| Bài tập 11: Mặt tiền của một ngôi biệt thự có 8 cây cột hình trụ tròn, tất cả đều có chiều cao 4,2 m. Trong số các cây đó, có hai cây cột trước đại sảnh đường kính bằng 40 cm, sáu cây cột còn lại phân bố đều hai bên đại sảnh và chúng đều có đường kính bằng 26 cm. Chủ nhà thuê nhân công để sơn các cây cột bằng một loại sơn giả đá, biết giá thuê là 380 000/1 m2 (kể cả vật liệu sơn và thi công). Hỏi người chủ phải chi ít nhất bao nhiêu tiền để sơn hết các cây cột nhà đó (đơn vị đồng)? (lấy $\pi =3,14159$)
A. 11 833 000 đồng. B. 12 242 000 đồng. C. 10 405 000 đồng D. 13 657 000 đồng. |
Lời giải chi tiết
Tổng diện tích quy hoạnh xung quanh của 8 cây cột đó là
USD { { S } _ { xq } } = 2. \ left ( 2 \ pi. \ frac { 0,4 } { 2 }. 4,2 \ right ) + 6. \ left ( 2 \ pi. \ frac { 0,26 } { 2 }. 4,2 \ right ) = 9,912 \ pi c { { m } ^ { 2 } } $
Vậy số tiền cần phải chi là $T=380\text{ }000.{{S}_{xq}}\approx 11\text{ }833\text{ }000$ đồng. Chọn A.
| Bài tập 12: Một xưởng sản xuất muốn tạo ra những chiếc đồng hồ cát bằng thủy tinh có dạng hình trụ, phần chứa cát là hai nửa hình cầu bằng nhau. Hình vẽ bên với các kích thước đã cho là bản thiết kế thiết diện qua trục của chiếc đồng hồ này (phần tô màu làm bằng thủy tinh). Khi đó, lượng thủy tinh làm chiếc đồng hồ cát gần nhất với giá trị nào trong các giá trị sau
A. 602,2 cm3. B. 1070,8 cm3. C. 6021,3 cm3. D. 711,6 cm3. |
Lời giải chi tiết
Thể tích của khối trụ là USD { { V } _ { 1 } } = \ pi { { r } ^ { 2 } } h = \ pi. 6, { { 6 } ^ { 2 } }. 13,2 = 1806,39 c { { m } ^ { 3 } } $
Thể tích khối cầu chứa cát là USD { { V } _ { 2 } } = \ frac { 4 } { 3 } \ pi { { R } ^ { 3 } } = \ frac { 4 } { 3 } \ pi. { { \ left ( \ frac { 13,2 – 2 } { 2 } \ right ) } ^ { 3 } } = 735,62 c { { m } ^ { 3 } } $
Vậy lượng thủy tinh cần phải làm là $V={{V}_{1}}-{{V}_{2}}=1070,77c{{m}^{3}}.$ Chọn B.
| Bài tập 13: : Cho hình chóp tam giác đều S.ABC có cạnh AB bằng a, góc tạo bởi hai mặt phẳng (SAB) và (ABC) bằng 600. Diện tích xung quanh của hình trụ có đường tròn đáy ngoại tiếp tam giác ABC và chiều cao bằng chiều cao của hình chóp là
A. $\frac{\sqrt{2}\pi {{a}^{2}}}{3}.$ B. $\frac{\sqrt{2}\pi {{a}^{2}}}{6}.$ C. $\frac{\sqrt{3}\pi {{a}^{2}}}{3}.$ D. $\frac{\sqrt{3}\pi {{a}^{2}}}{6}.$ |
Lời giải chi tiết
Gọi O là trọng tâm tam giác USD ABC \ Rightarrow SO \ bot \ left ( ABC \ right ) USD
Gọi M là trung điểm $ AB \ Rightarrow OM \ bot AB \ Rightarrow AB \ bot \ left ( SMO \ right ) USD
Khi đó $ \ left ( \ widehat { \ left ( SAB \ right ) ; \ left ( ABC \ right ) } \ right ) = \ left ( \ widehat { SM ; OM } \ right ) = \ widehat { SMO } = { { 60 } ^ { 0 } } $
Tam giác ABC đều có $ AB = a \ Rightarrow OC = \ frac { a \ sqrt { 3 } } { 3 } ; OM = \ frac { a \ sqrt { 3 } } { 6 } $
Tam giác SMO vuông tại O, có USD SO = OM.tan { { 60 } ^ { \ circ } } = \ frac { a } { 2 } $
Bán kính đường tròn ngoại tiếp ΔABC là USD R = OC = \ frac { a \ sqrt { 3 } } { 3 } $
Vậy diện tích xung quanh hình trụ là ${{S}_{xq}}=2\pi Rh=2\pi .\frac{a\sqrt{3}}{3}.\frac{a}{2}=\frac{\sqrt{3}\pi {{a}^{2}}}{3}.$ Chọn C.
| Bài tập 14: Cho hình chóp tứ giác đều S.ABCD có cạnh đáy bằng 2, góc giữa cạnh bên SA và mặt đáy bằng 30°. Gọi S là diện tích toàn phần của hình trụ có một đường tròn đáy là đường tròn nội tiếp hình vuông ABCD và chiều cao bằng chiều cao của hình chóp S.ABCD. Khẳng định nào dưới đây là đúng?
A. $S\approx 10,181.$ B. $S\approx 11,413.$ C. $S\approx 13,285.$ D. $S\approx 12,669.$ |
Lời giải chi tiết

Gọi O là tâm hình vuông vắn ABCD $ \ Rightarrow SO \ bot \ left ( ABCD \ right ) USD
Ta có $ \ left ( \ widehat { SA ; \ left ( ABCD \ right ) } \ right ) = \ left ( \ widehat { SA ; OA } \ right ) = \ widehat { SAO } = { { 30 } ^ { \ circ } } $
Tam giác SAO vuông tại O, có USD SO = OA. \ tan { { 30 } ^ { \ circ } } = \ frac { \ sqrt { 6 } } { 3 } $
Bán kính đường tròn nội tiếp hình vuông vắn ABCD là $ R = \ frac { AB } { 2 } = 1 USD
Vậy diện tích quy hoạnh toàn phần cần tính là
${{S}_{{}}}=2\pi Rh+2\pi {{R}^{2}}=2\pi .1.\frac{\sqrt{6}}{3}+2\pi {{.1}^{2}}\approx 11,413.$ Chọn B.
| Bài tập 15: Một nhà máy sản xuất cần thiết kế một thùng sơn dạng hình trụ có nắp đậy với dung tích 1000 cm3. Bán kính của nắp đậy để nhà sản xuất tiết kiệm nguyên vật liệu nhất bằng
A. $10\sqrt[3]{\frac{5}{\pi }}\text{ }cm.$ B. $10\sqrt[{}]{\frac{5}{\pi }}\text{ }cm.$ C. $\sqrt[{}]{\frac{500}{\pi }}\text{ }cm.$ D. $\sqrt[3]{\frac{500}{\pi }}\text{ }cm.$ |
Lời giải chi tiết
Gọi R, h lần lượt là nửa đường kính đáy và chiều cao hình tròn trụ
Thể tích khối trụ là $ V = \ pi { { R } ^ { 2 } } h = 1000 \ xrightarrow { { } } h = \ frac { 1000 } { \ pi { { R } ^ { 2 } } } $
Yêu cầu bài toán tương tự với “ diện tích quy hoạnh toàn phần nhỏ nhất ”
Ta có USD { { S } _ { tp } } = 2 \ pi Rh + 2 \ pi { { R } ^ { 2 } } = 2 \ pi { { R } ^ { 2 } } + 2 \ pi R. \ frac { 1000 } { \ pi { { R } ^ { 2 } } } = 2 \ pi { { R } ^ { 2 } } + \ frac { 2000 } { R } \ xrightarrow { { } } f \ left ( R \ right ) USD
Tìm giá trị nhỏ nhất của hàm số USD f \ left ( R \ right ) = 2 \ pi { { R } ^ { 2 } } + \ frac { 2000 } { R } $
• Cách 1. Khảo sát hàm số, với R > 0
• Cách 2. Áp dụng bất đẳng thức Cô-si, ta được
USD 2 \ pi { { R } ^ { 2 } } + \ frac { 2000 } { R } = 2 \ pi { { R } ^ { 2 } } + \ frac { 1000 } { R } + \ frac { 1000 } { R } \ ge 3 \ sqrt [ 3 ] { 2 \ pi { { R } ^ { 2 } }. \ frac { 1000 } { R }. \ frac { 1000 } { R } } = 3 \ sqrt [ 3 ] { 2 \ pi. { { \ left ( 1000 \ right ) } ^ { 2 } } } $
Dấu bằng xảy ra khi và chỉ khi $2\pi {{R}^{2}}=\frac{1000}{R}\Leftrightarrow R=\sqrt[3]{\frac{500}{\pi }}\text{ }cm.$ Chọn D.
Source: http://139.180.218.5
Category: tản mạn