Tính chất 3 đường trung trực của tam giác là nội dung trọng tâm trong toán hình lớp 7. Vậy tính chất của đường trung trực là gì ? Hãy cùng GiaiNgo khám phá nhé !
Đường trung trực của một tam giác luôn là kiến thức được sử dụng nhiều nhất trong các đề thi cuối kỳ. Vậy tính chất 3 đường trung trực của tam giác là gì? Hãy cùng GiaiNgo tìm hiểu nhé.
Bạn đang đọc: Tính chất 3 đường trung trực của tam giác? Bài tập SGK
Nội dung chính [ẩn đi]
Đường trung trực của tam giác là gì?
Tính chất 3 đường trung trực của tam giác
Đường trung trực là gì?
Trong hình học mặt phẳng, đường trung trực của một đoạn thẳng là đường vuông góc với đoạn thẳng tại trung điểm của đoạn thẳng đó .
Trong một tam giác, đường trung trực của mỗi cạnh của tam giác gọi là đường trung trực của tam giác. Trong kỹ năng và kiến thức toán hình học lớp 7, đường trung trực và những tính chất 3 đường trung trực của tam giác sẽ là phần trọng tâm trong học kỳ II .
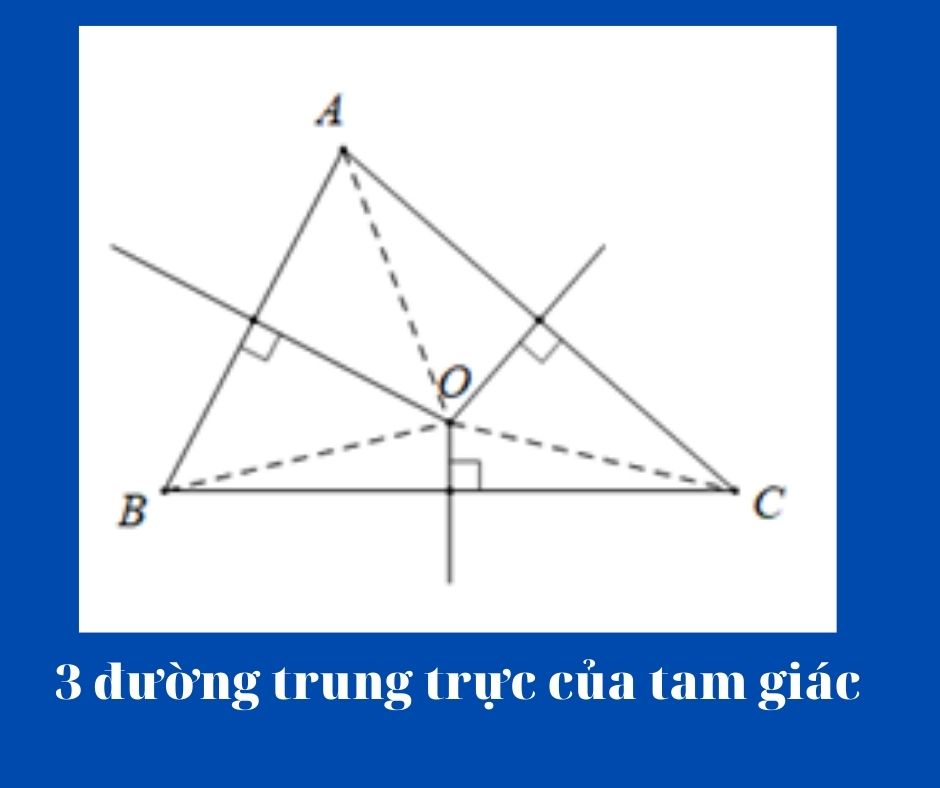
Tính chất 3 đường trung trực của tam giác
GiaiNgo sẽ nêu toàn bộ những tính chất 3 đường trung trực của tam một cách dễ nhớ nhất như sau :
- 3 đường trung trực của một tam giác cùng đi qua một điểm.
- Điểm này cách đều ba đỉnh của tam giác đó.
Bên cạnh đó, gọi O là giao điểm của ba đường trung trực của tam giác ABC. Ta có, điểm O cách đều ba đỉnh của tam giác đó. Do vậy, tam giác ABC có một đường tròn tâm O đi qua ba đỉnh A, B, C. Ta gọi đường tròn đó là đường tròn ngoại tiếp tam giác ABC .Đường tròn ngoại tiếp tam giác là tính chất đặc biệt quan trọng và khó nhớ nhất trong những tính chất 3 đường trung trực của tam giác. Mọi người nên quan tâm đến tính chất này .
Tính chất 3 đường trung trực của tam giác – định lý 1
Mọi tam giác đều có 3 đường trung trực. Trong đó, có 2 định lí quan trọng cần phải nhớ .
Định lí 1: Tính chất 3 đường trung trực của tam giác cân
Trong một tam giác cân, đường trung trực của cạnh đáy đồng thời là đường trung tuyến ứng với cạnh này .
Ví dụ : Trong một tam giác ABC cân tại ANếu AM là đường trung trực của cạnh BCSuy ra : MB = MC ( theo tính chất 3 đường trung trực của tam giác cân )
Tính chất 3 đường trung trực của tam giác – định lý 2
Định lí 2: Tính chất 3 đường trung trực của tam giác thường
Trong tam giác thường, 3 đường trung trực của tam giác cùng đi qua một điểm. Điểm này cách đều ba đỉnh của tam giác đó .
Ví dụ : Cho tam giác ABC trong đó :
- a là đường trung trực của BC
- b là đường trung trực của AC
- c là đường trung trực của AB
- b,c cắt nhau tại O
Từ đó ta thấy, O nằm trên đường thẳng aSuy ra : OA = OB = OC ( ( theo tính chất 3 đường trung trực của tam giác thường )
Bài tập liên quan đến tính chất 3 đường trung trực của tam giác
Bài tập 1
Cho hình vẽ cùng những dữ kiện đã lưu lại. Chứng minh ba điểm B, C, D thẳng hàng
Bài giải
Từ hình vẽ ta có :
+ DK là đường trung trực của AC ⇒ DA = DC .+ DI là đường trung trực của AB ⇒ DA = DB .+ Ta có : DI / / AC ( vì cùng ⏊ AB )Mà DK ⏊ AC ⇒ DK ⏊ DI
+ Xét ∆ ADK và ∆ CDK có :
- AD = DC
- AK = CK (gt)
- DK chung
⇒ ∆ ADK = ∆ CDK ( c. c. c )⇒ Góc ADK = góc CDK ( 2 góc tương ứng )⇒ Góc ADC = góc ADK + góc KDC = 2 lần góc ADK ( 1 )
+ Xét ∆ ADI và ∆ BDI có :
- AD = BD
- AI = BI (gt)
- DI chung
⇒ ∆ ADI = ∆ BDI ( c. c. c )⇒ Góc ADI = góc BDI ( 2 góc tương ứng )⇒ Góc ADB = góc ADI + góc IDB = 2 lần góc ADI ( 2 )Từ ( 1 ) và ( 2 ) ⇒ góc BDC = góc ABD + góc ADC = 2 lần góc IDK = 180 độ
⇒ B, C, D thẳng hàng .
Bài tập 2
Vẽ đường tròn đi qua ba đỉnh của tam giác ABC trong những trường hợp sau :
- Tam giác ABC có 3 góc nhọn
- Tam giác ABC có 1 góc vuông
- Tam giác ABC có một góc tù
Bài giải
Đường tròn đi qua ba đỉnh của tam giác ABC gọi là đường tròn ngoại tiếp tam giác đó. Ba đường trung trực của một tam giác cùng đi qua một điểm. Điểm này cách đều ba đỉnh của tam giác đó. Để vẽ đường tròn ta cần :+ Vẽ đường trung trực y của cạnh BC .
+ Vẽ dường trung trực x của cạnh AB.
+ x cắt y tại I là tâm của đường tròn cần vẽ .+ Vẽ đường tròn tâm I nửa đường kính IA .Nhận xét :
- Tam giác nhọn có tâm đường tròn ngoại tiếp nằm trong tam giác.
- Tam giác vuông có tâm đường tròn ngoại tiếp là trung điểm của cạnh huyền.
- Tam giác tù có tâm đường tròn ngoại tiếp nằm ngoài tam giác.
Bài tập 3
Chứng minh rằng : Điểm cách đều ba đỉnh của một tam giác vuông là trung điểm của cạnh huyền của tam giác đó. Từ đó, hãy tính độ dài đường trung tuyến xuất phát từ đỉnh góc vuông ( theo độ dài cạnh huyền của một tam giác vuông ) .
Bài giải
Giả sử ∆ ABC vuông tại A .d1 là đường trung trực cạnh AB ,d2 là đường trung trực cạnh AC .d1 cắt d2 tại M .
Khi đó M là điểm cách đều ba đỉnh của tam giác ABC và B, M, C thẳng hàng .+ M cách đều A, B, C⇒ MB = MC ⇒ M là trung điểm của cạnh BC ( đpcm )+ M là trung điểm của cạnh BC ( đpcm )Giả sử AM là trung tuyến của tam giác ABC
⇒ M là trung điểm của cạnh BC⇒ MB = MC = BC / 2Mà MA = MB = MC ( cmt )⇒ MA = BC / 2Vậy độ dài đường trung tuyến xuất phát từ đỉnh góc vuông bằng một nửa độ dài cạnh huyền .
Bài tập 4
Có một cụ thể máy ( mà đường viền ngoài là đường tròn ) bị gãy. Hãy dùng tính chất 3 đường trung trực của tam giác để xác lập nửa đường kính của đường viền này ?
Bài giải
Để xác lập được nửa đường kính ta cần xác lập được tâm của đường tròn chứa chi tiết cụ thể máy này. Ta xác định tâm như sau :+ Lấy ba điểm phân biệt A, B, C trên đường viền ngoài cụ thể máy .
+ Vẽ đường trung trực cạnh AB và cạnh BC. Hai đường trung trực này cắt nhau tại D .Khi đó D là tâm cần xác lập .+ Bán kính đường tròn cần tìm là độ dài đoạn DB ( hoặc DA hoặc DC ). Ta có hình vẽ minh họa
Bài tập 5
Cho tam giác ABC có đường phân giác AK của góc A. Biết rằng giao điểm của đường phân giác của tam giác ABK trùng với giao điểm ba đường trung trực của tam giác ABC .
Dựa vào những tính chất 3 đường trung trực của tam giác, hãy tìm số đo những góc của tam giác ABC .
Bài giải
Gọi O là giao điểm của 3 đường phân giác của tam giác ABKTheo đề bài, O là giao điểm của ba đường trung trực của tam giác ABCVậy OA = OB = OC và những tam giác AOB, AOC, BOC đều là những tam giác đều tại đỉnh O
Cho góc OAB = a thì góc ABC = KAB = 2 aVì AK là đường phân giác của góc BAC nên nếu góc KAB = 2 a thì góc BAC = 4 aTa có : ΔAOB = ΔCOB ⇒ AB = CBVậy tam giác ABC cân tại đỉnh B⇒ Góc BAC = góc BCA
Khi đó ta có : 2 a + 4 a + 4 a = 180 ° ⇒ 10 a = 180 ° ⇒ a = 18 °
Vậy số đo cách góc của tam giác ABC là góc A = góc C = 72°, góc B = 36°
Xem thêm: Tam giác.
Các bạn học viên quan tâm, những tính chất 3 đường trung trực của tam giác rất dễ nhớ nhưng cũng rất dễ nhầm lẫn. Các bạn nên nắm rõ và hiểu sâu thực chất của từng tính chất. Từ đó, vận dụng vào bài tập để hoàn toàn có thể nâng cao được kiến thức và kỹ năng và tư duy trong bộ môn hình học. Đừng quên cập nhập những kỹ năng và kiến thức khác cùng GiaiNgo qua những bài viết sau nhé !
Source: http://139.180.218.5
Category: tản mạn