Pi.

Byadnhacly

Th3 18, 2022

π. Về chữ cái Hy Lạp cùng tên, xem Bài viết này nói về hằng số toán học. Về vần âm Hy Lạp cùng tên, xem Pi ( vần âm ). Về những cách sử dụng khác, xem Pi ( khuynh hướng )

Số pi (ký hiệu: π), còn gọi là hằng số Archimedes, là một hằng số toán học có giá trị bằng tỷ số giữa chu vi của một đường tròn với đường kính của đường tròn đó. Hằng số này có giá trị xấp xỉ bằng 3,14. Nó được biểu diễn bằng chữ cái Hy Lạp π từ giữa thế kỷ XVIII.

π là một số vô tỉ, nghĩa là nó không thể được biểu diễn chính xác dưới dạng tỉ số của hai số nguyên. Nói cách khác, nó là một số thập phân vô hạn không tuần hoàn. Hơn nữa, π còn là một số siêu việt – tức là nó không phải là nghiệm của bất kì đa thức với hệ số hữu tỉ nào. Tính siêu việt của π kéo theo sự vô nghiệm của bài toán cầu phương. Các con số trong biểu diễn thập phân của π dường như xuất hiện theo một thứ tự ngẫu nhiên, mặc dù người ta chưa tìm được bằng chứng nào cho tính ngẫu nhiên này.

Bạn đang đọc: Pi.

Trong hàng ngàn năm, những nhà toán học đã nỗ lực lan rộng ra tầm hiểu biết của con người về số π, đôi lúc bằng việc tính ra giá trị của nó với độ đúng chuẩn ngày càng cao. Trước thế kỷ XV, những nhà toán học như Archimedes và Lưu Huy đã sử dụng những kĩ thuật hình học, dựa trên đa giác, để ước đạt giá trị của π. Bắt đầu từ thế kỷ XV, những thuật toán mới dựa trên chuỗi vô hạn đã cách mạng hóa việc tính toán số π, được những nhà toán học như Madhava của Sangamagrama, Isaac Newton, Leonhard Euler, Carl Friedrich Gauss và Srinivasa Ramanujan sử dụng .

Trong thế kỷ XXI, các nhà toán học và các nhà khoa học máy tính đã khám phá ra những cách tiếp cận mới – kết hợp với sức mạnh tính toán ngày càng cao – để mở rộng khả năng biểu diễn thập phân của số π tới 1013 chữ số[1]. Tháng 10 năm 2014, kỷ lục này được nâng lên 13.300.000.000.000 chữ số bởi một nhóm nghiên cứu lấy tên là houkouonchi.[2] Các ứng dụng khoa học thông thường yêu cầu không quá 40 chữ số của π, do đó động lực của những tính toán này chủ yếu là tham vọng của con người muốn đạt tới những kỉ lục mới, nhưng những tính toán đó cũng được sử dụng để kiểm tra các siêu máy tính và các thuật toán tính nhân với độ chính xác cao.

Do định nghĩa của π liên hệ với đường tròn, ta hoàn toàn có thể tìm thấy nó trong nhiều công thức lượng giác và hình học, đặc biệt quan trọng là những công thức tương quan tới đường tròn, đường elip, hoặc hình cầu. Nó cũng Open trong những công thức của những ngành khoa học khác, như thiên hà học, triết lý số, thống kê, phân dạng, nhiệt động lực học, cơ học và điện từ học. Sự xuất hiện thoáng rộng của số π khiến nó trở thành một trong những hằng số toán học được biết đến nhiều nhất, cả trong lẫn ngoài giới khoa học : một số ít sách viết riêng về số π đã được xuất bản ; ngày số pi ; báo chí truyền thông thường đặt những tin tức về kỉ lục giám sát chữ số mới của π trên trang nhất. Một số người còn cố gắng nỗ lực ghi nhớ giá trị của π với độ đúng chuẩn ngày càng tăng, đạt tới kỉ lục trên 70.000 chữ số .
π.Chu vi của một đường tròn lớn hơn khoảng chừng 3 lần so với đường kính. Giá trị đúng mực gọi là số

π thông thường được định nghĩa là tỉ số giữa chu vi của đường tròn C với đường kính của nó d[3]:

\pi ={\frac {C}{d}}

Tỉ số C/d là hằng số, bất kể kích thước của đường tròn dù to hay nhỏ. Ví dụ, nếu một đường tròn có đường kính gấp đôi đường kính của một đường tròn khác thì nó cũng có chu vi lớn gấp đôi, bảo toàn tỉ số C/d. Định nghĩa này về π không phổ quát, bởi vì nó chỉ đúng trong hình học Euclid (phẳng) và không đúng trong hình học phi Euclid (cong)[3]. Vì lý do này, một số nhà toán học ưa dùng những định nghĩa khác về π dựa trên vi tích phân hoặc lượng giác vốn không phụ thuộc vào đường tròn. Một định nghĩa như thế là: π bằng hai lần số x dương, nhỏ nhất mà với nó cos(x) bằng 0[3][4].

π trong một tác phẩm xuất bản năm Leonhard Euler đã phổ biến cách dùng chữ cái Hy Lạptrong một tác phẩm xuất bản năm 1748

Ký hiệu được các nhà toán học sử dụng để biểu diễn tỉ số giữa chu vi của một đường tròn và đường kính của nó là chữ cái Hy Lạp π. Chữ cái này được biểu diễn bằng từ Latin pi[5]. Không được nhầm lẫn ký tự in thường π (hoặc dưới dạng chữ không có nét chân chữ π) với ký tự in hoa Π (Π trong toán học dùng để biểu diễn một tích dãy số hay dãy hàm).

Nhà toán học đầu tiên dùng π với định nghĩa như trên là William Jones, trong cuốn “Synopsis Palmariorum Matheseos” (tạm dịch, Nhập môn Toán học mới) năm 1706[6]. Cụ thể, ký tự π lần đầu tiên xuất hiện trong cụm từ “1/2 Periphery (π)” trong đoạn bàn về một đường tròn với bán kính bằng 1. Có thể ông đã chọn π bởi vì nó là chữ cái đầu tiên trong cách ký âm tiếng Hy lạp περιφέρεια của từ periphery (nghĩa là viền ngoài, cũng tức là chu vi)[7]. Jones viết rằng các phương trình của π được lấy từ “bản viết có sẵn của John Machin thiên tài“, dẫn đến phỏng đoán rằng Machin có lẽ đã sử dụng ký tự Hy Lạp này trước Jones, tuy nhiên không có bằng chứng trực tiếp về điều này[8]. Ngoài ra, ký tự π đã xuất hiện trước đó trong các ký hiệu hình học; chẳng hạn, vào năm 1631 William Oughtred đã dùng nó để biểu diễn nửa chu vi của hình tròn[8].

Sau khi Jones giới thiệu ký hiệu này năm 1706, nó đã không được các nhà toán học khác chấp nhận; thay vào đó họ thường dùng chữ cái c hoặc p[8]. Điều này thay đổi khi Euler bắt đầu dùng nó năm 1736. Vì Euler thường xuyên trao đổi thư từ với những nhà toán học khác trên toàn châu Âu, việc sử dụng ký tự Hy Lạp này lan rộng nhanh chóng[8]. Năm 1748, Euler sử dụng π trong cuốn sách rất phổ biến của ông, Introductio in analysin infinitorum (Dẫn nhập Giải tích vô hạn), trong đó ông viết: “để cho ngắn gọn chúng ta sẽ viết số này là π; nghĩa là, π bằng một nửa chu vi của đường tròn bán kính bằng 1“.[9] Cách ký hiệu này kể từ đó được chấp nhận rộng rãi ở phương Tây[8].

π là một số vô tỉ, có nghĩa là nó không thể được biểu diễn dưới dạng tỉ số của hai số nguyên, như 22/7 hay các phân số khác thường được dùng để xấp xỉ π[10]. Vì π là số vô tỉ, biểu diễn thập phân của nó có số chữ số vô hạn, và nó không kết thúc ở dạng lặp lại vô hạn (vô hạn tuần hoàn) các chữ số. Có nhiều cách để chứng minh π là số vô tỉ; phương pháp thường dùng là sử dụng phép vi tích phân và phương pháp chứng minh bằng phản chứng. Mức độ xấp xỉ hóa π bằng số hữu tỉ (gọi là độ vô tỉ, hay hằng số Liouville-Roth) vẫn chưa được xác định chính xác; người ta ước lượng rằng độ vô tỉ của π lớn hơn e hoặc ln(2), nhưng nhỏ hơn số Liouville.[11].

π là một số siêu việt, tức là nó không phải là nghiệm của bất cứ phương trình đại số với hệ số hữu tỉ nào, như

120

−

{\displaystyle \scriptstyle {\frac {x^{5}}{120}}\,-\,{\frac {x^{3}}{6}}\,+\,x\,=\,0}

$\scriptstyle {\frac {x^{5}}{120}}\,-\,{\frac {x^{3}}{6}}\,+\,x\,=\,0$ [12]. Tính chất siêu việt của π có hai hệ quả quan trọng: thứ nhất, π không thể được biểu diễn bằng tổ hợp các số hữu tỉ và căn bậc n như

{\displaystyle \scriptstyle {\sqrt[{3}]{31}}}

$\scriptstyle {\sqrt[ {3}]{31}}$ hay

{\displaystyle \scriptstyle {\sqrt[{2}]{10}}}

$\scriptstyle {\sqrt[ {2}]{10}}$ [11]. Thứ hai, vì không có số siêu việt nào có thể được xác định bằng phép dựng hình bằng thước kẻ và compa, nên không thể giải bài toán “cầu phương hình tròn”. Nói cách khác, nếu chỉ sử dụng compa và thước kẻ thì không thể xây dựng một hình vuông mà diện tích của nó bằng diện tích của một hình tròn cho trước[13]. Cầu phương hình tròn là một trong những bài toán hình học quan trọng trong thời cổ đại[14]. Một số nhà toán học nghiệp dư thời hiện đại có lúc tuyên bố họ thành công dù điều này là không thể[15].

Các chữ số của π không có một quy luật rõ ràng nào và vượt qua những kiểm thử về tính ngẫu nhiên thống kê, trong đó có kiểm thử tính chuẩn tắc ; một số ít vô hạn được gọi là ‘ chuẩn tắc ‘ khi mọi dãy số khả dĩ ( với độ dài bất kỳ ) có tần suất Open là như nhau [ 16 ]. Người ta vẫn chưa thể khẳng định chắc chắn hoặc bác bỏ giả thuyết rằng π là ‘ chuẩn tắc ‘ [ 16 ]. Kể từ khi máy vi tính sinh ra, người ta đã tính được số π với số lượng chữ số lớn, đủ để thực thi những nghiên cứu và phân tích thống kê. Yasumasa Kanada đã triển khai những nghiên cứu và phân tích thống kê cụ thể về những chữ số thập phân của π, và thấy rằng chúng tương thích với tính chuẩn tắc ; ví dụ điển hình, tần suất Open những chữ số từ 0 tới 9 được sử dụng để kiểm tra ý nghĩa thống kê, và không tìm thấy dẫn chứng về một hình mẫu nào [ 17 ]. Bất chấp việc những chữ số của π đã vượt qua những bài kiểm tra về tính ngẫu nhiên, π có vẻ như vẫn chứa những dãy số có vẻ như có quy luật so với những người không phải nhà toán học, như điểm Feynman, là một dãy sáu chữ số 9 liên tục khởi đầu từ vị trí thứ 762 trong trình diễn thập phân của π [ 18 ] .

Phân số liên tục.

π được biểu diễn trong bức tranh khảm bên ngoài tòa nhà khoa Toán ở Đại học Công nghệ Berlin.Hằng sốđược trình diễn trong bức tranh khảm bên ngoài tòa nhà khoa Toán ởGiống như toàn bộ những số vô tỉ khác, π không hề được màn biểu diễn bằng một phân số thường ; nhưng mặt khác, mọi số vô tỉ, gồm có cả π, hoàn toàn có thể được màn biểu diễn bởi một chuỗi vô hạn những phân số lồng vào nhau, được gọi là phân số liên tục :

\pi =3+\textstyle {\frac {1}{7+\textstyle {\frac {1}{15+\textstyle {\frac {1}{1+\textstyle {\frac {1}{292+\textstyle {\frac {1}{1+\textstyle {\frac {1}{1+\textstyle {\frac {1}{1+\ddots }}}}}}}}}}}}}}

Chặt cụt phân số liên tục này ở bất kỳ điểm nào sẽ tạo nên một phân số xê dịch với π ; hai phân số như vậy ( 22/7 và 355 / 113 ) từng được sử dụng trong lịch sử dân tộc để tính gần đúng hằng số này. Các số gần đúng được sinh ra theo cách này là được gọi là ‘ giao động hữu tỉ tốt nhất ‘ ; nghĩa là, chúng gần với π hơn bất kỳ phân số nào khác có mẫu số bằng hoặc nhỏ hơn [ 19 ]. Mặc dù phân số liên tục đơn thuần cho π ( ở trên ) không bộc lộ một nguyên tắc nào [ 20 ], những nhà toán học đã mày mò ra vài phân số liên tục tổng quát ( tổng quát hóa phân số liên tục thường trong dạng chính tắc ) có quy luật, ví dụ điển hình [ 21 ] :

\pi =\textstyle {\cfrac {4}{1+\textstyle {\frac {1^{2}}{2+\textstyle {\frac {3^{2}}{2+\textstyle {\frac {5^{2}}{2+\textstyle {\frac {7^{2}}{2+\textstyle {\frac {9^{2}}{2+\ddots }}}}}}}}}}}}=3+\textstyle {\frac {1^{2}}{6+\textstyle {\frac {3^{2}}{6+\textstyle {\frac {5^{2}}{6+\textstyle {\frac {7^{2}}{6+\textstyle {\frac {9^{2}}{6+\ddots }}}}}}}}}}=\textstyle {\cfrac {4}{1+\textstyle {\frac {1^{2}}{3+\textstyle {\frac {2^{2}}{5+\textstyle {\frac {3^{2}}{7+\textstyle {\frac {4^{2}}{9+\ddots }}}}}}}}}}

Giá trị gần đúng.

Một số giá trị gần đúng của π gồm có :

Dạng phân số: Các giá trị xấp xỉ bao gồm (theo thứ tự độ chính xác tăng dần) ${\frac {22}{7}},{\frac {333}{106}},{\frac {355}{113}},{\frac {52163}{16604}},{\frac {103993}{33102}}$ ${\frac {30246273033735921}{9627687726852338}}$ [19].
Dạng thập phân: 100 chữ số thập phân đầu của π là 3,14159 26535 89793 23846 26433 83279 50288 41971 69399 37510 58209 74944 59230 78164 06286 20899 86280 34825 34211 70679….[22]
Dạng căn: ${\sqrt {9,86960440109}},{\sqrt[{3}]{31,00627668}}$
Dạng nhị phân:
Dạng thập lục phân:[23]
Dạng lục thập phân: Xấp xỉ cơ số 60 của số pi là 3,8:29:44:1

Thời Cổ đại.

Kim tự tháp Kheops ở Giza ( kiến thiết xây dựng vào khoảng chừng thời hạn 2589 – 2566 tr. CN ) được phong cách thiết kế với chu vi khoảng chừng 1760 cubit ( 1 cubit bằng khoảng chừng 0,5 mét ) và chiều cao khoảng chừng 280 cubit. Dựa vào tỉ lệ 1760 / 280 ≈ 6.2857, xê dịch bằng τ = 2 π ≈ 6.2832, 1 số ít nhà Ai Cập học Kết luận rằng những nhà thiết kế xây dựng kim tự tháp đã biết đến số π và chủ ý phong cách thiết kế kim tự tháp theo tỉ lệ đường tròn [ 24 ]. Tuy nhiên nhiều người không đống ý với quan điểm này và chứng minh và khẳng định mối quan hệ với số π đơn thuần là một sự trùng hợp, bởi không có dẫn chứng cho thấy những người kiến thiết xây dựng kim tự tháp đã biết đến số π, và kích cỡ của kim tự tháp còn dựa trên nhiều yếu tố khác [ 25 ] .Những ước đạt sớm nhất về π được tìm thấy ở Ai Cập và Babylon có niên đại từ thiên niên kỉ thứ 2 trước Công nguyên, với sai số tương đối cùng vào cỡ một Phần Trăm. Ở Babylon, một tấm đất sét có niên đại khoảng chừng 1900 – 1600 tr. CN đã ghi lại một phát biểu hình học, trong đó ám chỉ ước đạt số π bằng 25/8 = 3,1250 [ 26 ]. Ở Ai Cập, cuộn giấy Rhind, có niên đại khoảng chừng 1650 tr. CN, bản sao của một văn bản có từ khoảng chừng 1850 tr. CN, có ghi một công thức tính diện tích quy hoạnh hình tròn trụ, trong đó gán cho giá trị của π bằng ( 16/9 ) 2 ≈ 3,1605 [ 26 ] .

Ở Ấn Độ vào khoảng 600 năm trước Công nguyên, bộ Kinh Shulba (viết bằng tiếng Phạn với nhiều nội dung toán học) đã cho số π bằng (9785/5568)2 ≈ 3,088.[27]. Vào năm 150 tr.CN hoặc sớm hơn, có tài liệu của Ấn Độ đánh giá π bằng

{\displaystyle \scriptstyle {\sqrt {10}}}

$\scriptstyle {\sqrt {10}}$ ≈ 3,1622[28].

Hai bài thơ trong Kinh thánh Hebrew (được viết giữa thế kỷ VIII và thế kỷ III tr.CN) mô tả một hồ nước dùng trong nghi lễ tại Đền Solomon có đường kính 10 cubit và chu vi 30 cubit, bài thơ ngụ ý rằng π bằng 3 nếu hồ có hình tròn[29][30]. Học giả người Do Thái Rabbi Nehemiah giải thích sự sai khác nằm ở độ dày của hồ. Công trình về hình học của ông, Mishnat ha-Middot, viết vào khoảng năm 150 CN và coi π bằng 21/7[31].

Thời kì của phép xê dịch đa giác.

π có thể ước lượng bằng cách tính chu vi của các đa giác nội tiếp và ngoại tiếp đường tròn.hoàn toàn có thể ước đạt bằng cách tính chu vi của những đa giác nội tiếp và ngoại tiếp đường tròn .

Thuật toán chặt chẽ đầu tiên được ghi chép để tính giá trị của π là một cách tiếp cận hình học sử dụng đa giác, được phát minh vào khoảng năm 250 tr. CN bởi nhà toán học người Hy Lạp Archimedes[32]. Thuật toán đa giác của Archimedes thống trị suốt hơn 1000 năm, khiến cho π đôi khi được gọi là “hằng số Archimedes”[33]. Archimedes đã tính toán các giới hạn trên và dưới của π bằng cách vẽ hai đa giác đều có cùng số cạnh, một nội tiếp và một ngoại tiếp với cùng một hình tròn, sau đó từ từ tăng số cạnh lên gấp đôi cho đến khi đạt đến đa giác đều 96 cạnh. Bằng cách tính chu vi của các đa giác này, ông chứng minh rằng 223/71 < π < 22/7 (3,1408 < π < 3,1429). Có thể chính cận trên 22/7 của phép tính đã dẫn đến việc nhiều người cho rằng π bằng 22/7[34]. Khoảng năm 150 CN, nhà khoa học Hy Lạp-La Mã Ptolemaeus, trong bộ Almagest của mình, đã đưa ra giá trị π bằng 3,1416, có lẽ là lấy lại kết quả tính toán của Archimedes hoặc của Apollonius xứ Pergaeus[35]. Các nhà toán học, bằng cách sử dụng thuật toán đa giác, đã tính được tới chữ số thứ 39 của π vào năm 1630, một kỉ lục mà đến năm 1699 mới được phá vỡ khi chữ số thứ 71 được tính ra bằng phương pháp chuỗi vô hạn[36].

π.Archimedes đã phát triển cách tiếp cận đa giác để tính toán số

Ở Trung Hoa cổ đại, các giá trị của π bao gồm 3,1547 (khoảng năm thứ nhất của Công Nguyên),

{\displaystyle \scriptstyle {\sqrt {10}}}

(100 của Công Nguyên, xấp xỉ 3,1623) và 142/45 (thế kỷ thứ III, xấp xỉ 3,1556)[37]. Vào khoảng năm 265, nhà toán học triều Tào Ngụy tên là Lưu Huy đã phát minh ra thuật toán lặp dựa trên đa giác (thuật toán π Lưu Huy) và sử dụng nó với một đa giác 3072 cạnh để thu được giá trị của π bằng 3,1416[38][39]. Cũng chính Lưu Huy sau đó đã phát triển một phương pháp nhanh hơn để tính π và thu được giá trị 3,14 với một đa giác 96 cạnh, bằng cách lợi dụng tính chất là hiệu diện tích các đa giác liên tiếp tạo nên một dãy cấp số nhân với hệ số 4[38]. Vào khoảng năm 480, một nhà toán học Trung Quốc khác là Tổ Xung Chi đã tính toán ra π ≈ 355/113, sử dụng thuật toán Lưu Huy cho đa giác 12.288 cạnh. Với giá trị chính xác ở bảy chữ số thập phân đầu tiên, giá trị 3,141592920… là giá trị gần đúng chính xác nhất của π mà con người tính được trong suốt hơn 800 năm sau đó[40].

Trong khi đó, nhà thiên văn người Ấn Độ Aryabhata sử dụng giá trị 3,1416 trong sách Āryabhaṭīya của ông (năm 499 của Công Nguyên)[41]. Fibonacci vào khoảng năm 1220 đã tính ra giá trị 3,1418 bằng một phương pháp đa giác khác với phương pháp của Archimedes[42]. Văn hào người Ý Dante dường như đã sử dụng giá trị của π là

3
+

{\displaystyle \scriptstyle 3+{\sqrt {2}}/10}

$\scriptstyle 3+{\sqrt {2}}/10$ ≈ 3,14142[42].

Nhà thiên văn Ba Tư Jamshīd al-Kāshī đã tìm ra 16 chữ số vào năm 1424 bằng cách sử dụng đa giác có 3 × 228 cạnh [ 43 ] [ 44 ], xác lập một kỉ lục quốc tế mới sống sót được khoảng chừng 180 năm [ 45 ]. Nhà toán học Pháp François Viète vào năm 1579 tính được 9 chữ số bằng một đa giác 3 × 217 cạnh [ 45 ]. Nhà toán học xứ Vlaanderen Adriaan van Roomen đạt tới chữ số 15 vào năm 1593 [ 45 ]. Năm 1596, nhà toán học người Hà Lan Ludolph van Ceulen đạt tới 20 chữ số, một kỉ lục được chính ông về sau nới rộng lên thành 35 chữ số ( tác dụng số π được gọi là ” số Ludolph ” trong tiếng Đức cho tới tận đầu thế kỷ XX ) [ 46 ]. Khoa học gia người Hà Lan Willebrord Snellius đạt tới 34 chữ số vào năm 1621 [ 47 ] và nhà thiên văn học người Áo Christoph Grienberger đạt tới 39 chữ số vào năm 1630 [ 48 ], đến nay vẫn là hiệu quả đúng mực nhất được tính thủ công bằng thuật toán sử dụng đa giác .

Những chuỗi số vô hạn.

Việc tính toán số π được cách mạng hóa bởi sự phát triển kĩ thuật chuỗi số vô hạn trong các thế kỷ XVI và XVII. Một chuỗi vô hạn là một tổng các số hạng của một dãy vô hạn[49]. Chuỗi vô hạn cho phép các nhà toán học tính toán π với độ chính xác lớn hơn nhiều độ chính xác đạt được từ phương pháp của Archimedes và các kĩ thuật hình học khác[49]. Mặc dù chuỗi vô hạn được sử dụng cho số π nổi tiếng nhất bởi các nhà toán học châu Âu như James Gregory và Gottfried Leibniz, cách tiếp cận này được khám phá lần đầu tiên ở Ấn Độ vào giữa những năm 1400 và 1500 CN[50]. Bản ghi chép đầu tiên mô tả một chuỗi vô hạn có thể tính toán số π nằm trong một bài thơ tiếng Phạn của nhà thiên văn Ấn Độ Nilakantha Somayaji trong tập Tantrasamgraha của ông, ra đời khoảng năm 1500[51]. Trong tập sách, chuỗi này được chép lại mà không có chứng minh, nhưng phép chứng minh đã được trình bày trong một công trình Ấn Độ sau đó, Yuktibhāṣā, do Jyesthadeva biên soạn vào khoảng năm 1530. Nilakantha quy chuỗi này là phát hiện của một nhà toán học Ấn Độ trước đó, Madhava của Sangamagrama, người sống trong khoảng những năm 1350-1425[51]. Một số chuỗi vô hạn được mô tả, bao gồm các chuỗi sin, tang, và cosin, ngày nay được biết dưới tên chuỗi Madhava hay chuỗi Gregory-Leibniz[51]. Madhava đã sử dụng những chuỗi vô hạn để đánh giá π tới 11 chữ số vào khoảng năm 1400, nhưng kỉ lục này đã bị đánh bại bởi một thuật toán đa giác của Jamshīd al-Kāshī năm 1430[52].

π tới 15 chữ số, về sau viết trong một lá thư rằng “Tôi lấy làm hổ thẹn để kể với anh bao nhiêu con số tôi đã thực hiện cho những tinh toán này”[53].Isaac Newton đã sử dụng chuỗi vô hạn để tính toántới 15 chữ số, về sau viết trong một lá thư rằng “Tôi lấy làm hổ thẹn để kể với anh bao nhiêu con số tôi đã thực hiện cho những tinh toán này”Dãy số vô hạn tiên phong được mày mò ở châu Âu là một tích vô hạn ( thay vì một tổng vô hạn, vốn thông dụng hơn trong phép tính số π ) được tìm thấy bởi nhà toán học Pháp François Viète năm 1593 [ 54 ] :

{\frac 2\pi }={\frac {{\sqrt 2}}2}\times {\frac {{\sqrt {2+{\sqrt 2}}}}2}\times {\frac {{\sqrt {2+{\sqrt {2+{\sqrt 2}}}}}}2}\times \cdots

Dãy số vô hạn thứ hai ở châu Âu của John Wallis ( 1655 ) cũng là một tích vô hạn nữa [ 54 ]. Khám phá ra phép vi tích phân, bởi nhà khoa học Anh Isaac Newton và nhà toán học Đức Leibniz vào thập niên 1660 đã dẫn tới sự tăng trưởng nhiều chuỗi vô hạn để nhìn nhận π. Chính Newton cũng dùng một chuỗi arcsin để tính ra một xê dịch 15 chữ số cho số π vào khoảng chừng năm 1665 hoặc 1666, và về sau này viết rằng ” Tôi lấy làm hổ thẹn để kể với anh bao nhiêu số lượng tôi đã thực thi cho những tinh toán này, chẳng có việc gì hơn để làm vào lúc đó cả ” [ 53 ] .Ở châu Âu, công thức Madhava được mày mò lại bởi nhà toán học Scotland James Gregory năm 1671, và bởi Leibniz năm 1674 [ 55 ] [ 56 ] :

\arctan z=z-{\frac {z^{3}}{3}}+{\frac {z^{5}}{5}}-{\frac {z^{7}}{7}}+\cdots

Công thức này, tức chuỗi Gregory-Leibniz, tương đương

{\displaystyle \scriptstyle \pi /4}

$\scriptstyle \pi /4$ khi đánh giá với z = 1[56]. Năm 1699, nhà toán học Anh Abraham Sharp sử dụng chuỗi Gregory-Leibniz để tính π tới 71 chữ số, phá vỡ kỉ lục trước đó với 39 chữ số xác lập bởi một thuật toán đa giác[57]. Chuỗi Gregory-Leibniz đơn giản, nhưng nó hội tụ rất chậm (có nghĩa là, tiệm cận với giá trị chính xác một cách từ từ qua từng số hạng), do đó người ta không dùng nó trong các phép tính toán số π hiện đại[58].

Năm 1706 John Machin sử dụng chuỗi Gregory-Leibniz để tạo nên một thuật toán quy tụ nhanh hơn nhiều [ 59 ] :

{\frac {\pi }{4}}=4\,\arctan {\frac {1}{5}}-\arctan {\frac {1}{239}}

Machin đã đạt tới 100 chữ số của π với công thức này [ 60 ]. Các nhà toán học khác tạo nên những biến thể của nó, ngày này được biết dưới tên ” những công thức kiểu Machin “, được dùng để thiết lập một số ít kỉ lục tiếp theo cho số chữ số của π [ 60 ]. Các công thức kiểu Machin duy trì là chiêu thức được biết đến nhiều nhất để thống kê giám sát π khi tiến tới ngưỡng cửa kỉ nguyên máy tính, và chúng đã tạo nên những kỉ lục trong 250 năm, lên đến đỉnh điểm vào một phép gần đúng 620 chữ số năm 1946 bởi Daniel Ferguson – đây chính là hiệu quả cao nhất mà con người từng đạt được mà không có sự trợ giúp của một thiết bị thống kê giám sát nào [ 61 ] .Một kỉ lục đáng quan tâm được thiết lập bởi thiên tài giám sát Zacharias Dase vào năm 1844 khi ông 20 tuổi. Ông đã sử dụng một công thức kiểu Machin để giám sát 200 chữ số của π trong đầu dưới sự chỉ huy của nhà toán học Đức Carl Friedrich Gauss [ 62 ]. Nhà toán học Anh William Shanks nổi tiếng vì dành 15 năm để thống kê giám sát π tới 707 chữ số ( hoàn thành xong năm 1873 ), nhưng về sau người ta tìm thấy một lỗi sai ở chữ số thứ 528, kéo toàn bộ những số đằng sau sai theo [ 62 ] .

Tốc độ quy tụ.

Một số chuỗi vô hạn cho π quy tụ nhanh hơn những chuỗi khác. Cho trước hai chuỗi vô hạn cho π, những nhà toán học thường thì sử dụng chuỗi quy tụ nhanh hơn bởi như thế đồng nghĩa tương quan với việc giảm được số lượng phép tính cho bất kể độ đúng mực nhu yếu nào [ 63 ]. Một chuỗi vô hạn cho π là chuỗi Gregory-Leibniz : [ 64 ]

\pi ={\frac {4}{1}}-{\frac {4}{3}}+{\frac {4}{5}}-{\frac {4}{7}}+{\frac {4}{9}}-{\frac {4}{11}}+{\frac {4}{13}}-\cdots

Khi những số hạng riêng không liên quan gì đến nhau của chuỗi vô hạn này được cộng thêm vào tổng, tổng số tiến gần hơn từ từ tới π, và – với một số lượng số hạng đủ – nó sẽ tiến đến π gần như mong ước. Nó quy tụ khá chậm, sau 500 000 số hạng, nó chỉ sinh ra 5 chữ số đúng chuẩn của π [ 65 ] .Một chuỗi vô hạn cho π được công bố bởi Nilakantha vào thế kỷ XV quy tụ nhanh hơn nhiều chuỗi Gregory-Leibniz [ 66 ] :

\pi =3+{\frac {4}{2\times 3\times 4}}-{\frac {4}{4\times 5\times 6}}+{\frac {4}{6\times 7\times 8}}-{\frac {4}{8\times 9\times 10}}+\cdots

Bảng sau so sánh vận tốc quy tụ của hai chuỗi này :

Chuỗi vô hạn cho π	Sau số hạng thứ nhất	Sau số hạng thứ 2	Sau số hạng thứ 3	Sau số hạng thứ 4	Sau số hạng thứ 5	Hội tụ tới:
$\scriptstyle \pi ={\frac {4}{1}}-{\frac {4}{3}}+{\frac {4}{5}}-{\frac {4}{7}}+{\frac {4}{9}}-{\frac {4}{11}}+{\frac {4}{13}}\cdots .$	4,0000	2,6666…	3,4666…	2,8952…	3,3396…	π = 3,1415…
$\scriptstyle \pi ={{3}}+{\frac {{4}}{2\times 3\times 4}}-{\frac {{4}}{4\times 5\times 6}}+{\frac {{4}}{6\times 7\times 8}}\cdots .$	3,0000	3,1666…	3,1333…	3,1452…	3,1396…	π = 3,1415…

Sau 5 số hạng, tổng của chuỗi Gregory-Leibniz nằm trong sai số tuyệt đối cỡ 0,2 của π, trong khi tổng của chuỗi Nilakantha sai số chỉ cỡ 0,002. Như vậy chuỗi Nilakantha quy tụ nhanh hơn và hữu dụng hơn trong việc tính toán số π. Những chuỗi thậm chí còn quy tụ còn nhanh hơn gồm có những chuỗi kiểu Machin và chuỗi Chudnovsky, trong đó chuỗi Chudnovsky tạo ra 14 chữ số thập phân đúng cho mỗi số hạng thêm vào [ 63 ] .

Tính vô tỉ và tính siêu việt.

Không phải toàn bộ những văn minh toán học tương quan tới π đều nhằm mục đích vào việc tăng độ đúng mực của phép giao động. Khi Euler giải Bài toán Basel vào năm 1735, tìm ra giá trị đúng mực của tổng những căn bậc hai, ông đã thiết lập một mối liên hệ giữa π và những số nguyên tố mà về sau góp thêm phần vào sự tăng trưởng và nghiên cứu và điều tra hàm Riemann zeta [ 67 ] :

{\frac {\pi ^{2}}{6}}={\frac {1}{1^{2}}}+{\frac {1}{2^{2}}}+{\frac {1}{3^{2}}}+{\frac {1}{4^{2}}}+\cdots

Nhà khoa học Thụy Sĩ Johann Heinrich Lambert vào năm 1761 chứng minh rằng π là số vô tỉ, có nghĩa nó không bằng tỉ số của bất kì hai số hữu tỉ nào[10]. Phép chứng minh của Lambert khai thác một biểu diễn phân số liên tục của hàm tang[68]. Nhà toán học Pháp Adrien-Marie Legendre vào năm 1794 chứng tỏ rằng π2 cũng là số vô tỉ. Năm 1882, nhà toán học Đức Ferdinand von Lindemann chứng tỏ rằng π là số siêu việt, xác nhận một phỏng đoán được cả Legendre và Euler đưa ra trước đó[69]

Kỉ nguyên máy tính và những thuật toán lặp.

Sự phát triển của máy tính vào giữa thế kỷ XX một lần nữa đã cách mạng hóa cuộc săn lùng những chữ số của π. Các nhà toán học Hoa Kỳ là John Wrench và Levi Smith đã đạt tới 1120 chữ số vào năm 1949 với một máy tính bàn[70]. Sử dụng một chuỗi vô hạn arctang, một nhóm đứng đầu bởi George Reitwiesner và John von Neumann đã đạt được 2037 chữ số với một phép tính đòi hỏi 70 giờ làm việc của máy tính ENIAC[71]. Kỉ lục, luôn dựa vào các chuỗi arctang, liên tục bị phá vỡ sau đó (7 480 chữ số năm 1957, 10 000 chữ số năm 1958, 100 000 năm 1961) cho đến khi 1 triệu chữ số đạt được vào năm 1973[72].

Hai tân tiến khác khoảng chừng năm 1980 một lần nữa tăng cường năng lực tính toán số π. Thứ nhất, tò mò ra những thuật toán lặp để tính π nhanh hơn nhiều những chuỗi vô hạn ; và thứ hai, sự ý tưởng ra thuật toán nhân nhanh cho phép nhân những số lớn một cách nhanh gọn [ 73 ]. Những thuật toán như vậy là đặc biệt quan trọng quan trọng trong việc tính toán số π thời tân tiến, bởi hầu hết thời hạn quản lý và vận hành máy tính là dành cho những phép nhân [ 74 ]. Chúng gồm có thuật toán Karatsuba, phép nhân Toom-Cook, và những chiêu thức dựa trên biến hóa Fourier [ 75 ] .
Khởi tạo

\scriptstyle a_{0}=1\quad b_{0}={\frac {1}{{\sqrt 2}}}\quad t_{0}={\frac {1}{4}}\quad p_{0}=1

Thuật toán lặp Gauss-Legendre : Khởi tạoLặp

\scriptstyle a_{{n+1}}={\frac {a_{n}+b_{n}}{2}}\quad \quad b_{{n+1}}={\sqrt {a_{n}b_{n}}}

\scriptstyle t_{{n+1}}=t_{n}-p_{n}(a_{n}-a_{{n+1}})^{2}\quad \quad p_{{n+1}}=2p_{n}

Sau đó một phép ước đạt π được tính từ

\scriptstyle \pi \approx {\frac {(a_{n}+b_{n})^{2}}{4t_{n}}}

Các thuật toán lặp được công bố một cách độc lập trong năm 1975-1976 bởi nhà vật lý Hoa Kỳ Eugene Salamin và nhà khoa học Australia Richard Brent[76]. Các thuật toán này chấm dứt sự phụ thuộc vào các chuỗi vô hạn. Một thuật toán lặp
(iterative algorithm) lặp lại một phép tính đặc trưng, mỗi lần lặp lại sử dụng đầu ra từ bước lặp trước làm đầu vào của nó, và sinh ra một kết quả trong mỗi bước hội tụ về giá trị mong muốn. Cách tiếp cận này thực ra đã được khám 160 năm trước đó bởi Carl Friedrich Gauss, trong một phương pháp mà ngày nay gọi là phương pháp AGM (arithmetic-geometric mean method, phương pháp trung bình hình học-đại số) hay thuật toán Gauss-Legendre[76]. Vì được sửa đổi bởi Salamin và Brent, nó cũng còn được gọi là thuật toán Brent-Salamin.

Các thuật toán lặp được sử dụng thoáng đãng sau 1980 bởi nó nhanh hơn những thuật toán chuỗi vô hạn : trong khi những chuỗi vô hạn thường tăng số chữ số đúng chuẩn từ từ một cách cộng thêm, những thuật toán lặp lại thường ” nhân ” số chữ số đúng chuẩn ở mỗi bước. Ví dụ, thuật toán Brent-Salamin nhân đôi số chữ số trong mỗi lần lặp. Năm 1984, hai bạn bè người Canada John và Peter Borwein tạo nên một thuật toán lặp nhân bốn lần số chữ số trong mỗi bước ; và năm 1987, một thuật toán nhân năm lần mỗi bước [ 77 ]. Các chiêu thức lặp được sử dụng bởi nhà toán học Nhật Bản Yasumasa Kanada để lập lên 1 số ít kỉ lục giữa 1995 và 2002 [ 78 ]. Sự quy tụ nhanh có được kèm theo một cái giá : những thuật toán lặp yên cầu bộ nhớ nhiều hơn đáng kể so với những chuỗi vô hạn [ 78 ] .

Động lực tính toán số π

.

π tăng nhanh chóng.Khi những nhà toán học mày mò ra những thuật toán mới, và máy tính trở nên sẵn dùng, số những chữ số được biết vềtăng nhanh gọn .Đối với hầu hết những tính toán số tương quan tới π, một chút ít chữ số thôi đã cung cấp độ đúng mực thiết yếu. Chẳng hạn, theo Jörg Arndt và Christoph Haenel, 39 chữ số là đủ để triển khai những đo lường và thống kê thiên hà học, bởi đây là độ đúng mực thiết yếu để tính thể tích thiên hà hiện biết với độ đúng mực cỡ một nguyên tử [ 79 ]. Bất chấp điều này, nhiều người đã thao tác rất khó khăn vất vả để giám sát π tới hàng nghìn, hàng triệu và nhiều hơn thế những chữ số [ 80 ]. Nỗ lực này một phần hoàn toàn có thể quy cho sự thúc ép con người phá vỡ những kỉ lục, và những thành tích như vậy với π thường Open trên trang nhất báo chí truyền thông trên khắp quốc tế [ 81 ] [ 82 ]. Chúng cũng có những quyền lợi thực tiễn, như thể kiểm tra những siêu máy tính, kiểm tra những thuật toán giải tích số ( gồm có những thuật toán nhân đúng mực cao ) ; và trong địa hạt toán học thuần túy, chúng phân phối tài liệu để nhìn nhận tính ngẫu nhiên những chữ số của π [ 83 ] .

Các chuỗi quy tụ nhanh.

π.Srinivasa Ramanujan, làm việc một mình ở Ấn Độ, đã tạo nên nhiều chuỗi số mới để tính sốCác phép tính số π văn minh không chỉ sử dụng duy nhất thuật toán lặp. Các chuỗi vô hạn mới được phát hiện vào những thập niên 1980 và 1990 cũng quy tụ nhanh không kém những thuật toán lặp, nhưng đơn thuần hơn và tốn ít bộ nhớ hơn [ 78 ]. Chúng đã manh nha Open vào năm 1914, khi nhà toán học Ấn Độ Srinivasa Ramanujan công bố hàng chục công thức mới cho số π, chúng đáng nhớ do tính thanh nhã, chiều sâu toán học và sự quy tụ nhanh [ 84 ]. Một trong những công thức của ông, dựa trên những phương trình module :

{\frac {1}{\pi }}={\frac {2{\sqrt 2}}{9801}}\sum _{{k=0}}^{\infty }{\frac {(4k)!(1103+26390k)}{(k!)^{4}396^{{4k}}}}

Chuỗi này hội tụ nhanh hơn rất nhiều hầu hết mọi chuỗi arctang, bao gồm cả công thức Machin[85]. Bill Gosper là người đầu tiên sử dụng nó để tạo nên những tiến bộ trong tính toán π, lập nên kỉ lục 17 triệu chữ số vào năm 1985[86]. Các công thức của Ramanujan báo trước các thuật toán hiện đại phát triển bởi anh em nhà Borwein và anh em nhà Chudnovsky[87]. Thuật toán Chudnovsky được phát triển vào năm 1987 là:

{\frac {1}{\pi }}=12\sum _{{k=0}}^{\infty }{\frac {(-1)^{k}(6k)!(13591409+545140134k)}{(3k)!(k!)^{3}640320^{{3k+3/2}}}}.\!

Nó sinh ra khoảng chừng 14 chữ số của π mỗi số hạng [ 88 ], và đã được dùng cho một vài phép tính lập kỉ lục về π, trong đó có kỉ lục vượt một tỉ chữ số năm 1989 bởi đồng đội nhà Chudnovsky. Vào ngày 31 tháng 9 năm 2012 [ 89 ] Fabrice Bellard đã lập kỉ lục khi sử dụng công thức Chudnovsky để tính chữ số thứ 2,7 nghìn tỉ của số π [ 90 ] trước khi bị Shigeru Kondo vượt mặt khi tính ra chữ số thứ 5 nghìn tỉ vào năm 2010 [ 91 ] và sau đó là chữ số thứ 10 nghìn tỉ của π vào năm 2011. [ 92 ]Năm 2006, nhà toán học Canada Simon Plouffe đã sử dụng ” thuật toán hệ thức nguyên PSLQ ” ( PSLQ : Partial Sum of Least Squares – tổng riêng phần của những bình phương cực tiểu ) để tạo ra một vài công thức mới cho π, tuân theo mẫu sau :

\pi ^{k}=\sum _{{n=1}}^{\infty }{\frac {1}{n^{k}}}\left({\frac {a}{q^{n}-1}}+{\frac {b}{q^{{2n}}-1}}+{\frac {c}{q^{{4n}}-1}}\right)

trong đó

{\displaystyle {\mathit {q}}}

${\mathit {q}}$ là hằng số Gelfond eπ,

{\displaystyle {\mathit {k}}}

${\mathit {k}}$ là một số lẻ, và

a
,
b
,
c

{\displaystyle {\mathit {a,b,c}}}

${\mathit {a,b,c}}$ là những số hữu tỉ mà Plouffe đưa vào[93].

Thuật toán miệng vòi.

Hai thuật toán được mày mò vào năm 1995 đã mở ra một hướng đi mới cho điều tra và nghiên cứu về số π. Chúng gọi là những thuật toán ” miệng vòi ” ( spigot algorithms ) do tại, giống như nước nhỏ giọt khỏi một miệng vòi, chúng tạo ra từng chữ số riêng không liên quan gì đến nhau của π không được tái sử dụng sau khi đã được tính ra [ 94 ] [ 95 ]. Điều này trái chiều với những chuỗi vô hạn hay những thuật toán lặp, là những thuật toán lưu giữ và sử dụng toàn bộ những chữ số trung gian cho đến khi tác dụng sau cuối được tạo ra [ 94 ] .

Các nhà toán học Hoa Kỳ Stan Wagon và Stanley Rabinowitz đã tạo nên một thuật toán miệng vòi đơn giản vào năm 1995[95][96][97]. Tốc độ của nó là tương đương với các thuật toán arctang, nhưng không nhanh bằng các thuật toán lặp[96].

Một thuật toán miệng vòi khác, thuật toán trích xuất chữ số Bailey-Borwein-Plouffe ( BBP digit extraction algorithm ), được phát hiện vào năm 1995 bởi Simon Plouffe [ 98 ] [ 99 ] :

\pi =\sum _{{i=0}}^{\infty }{\frac {1}{16^{i}}}\left({\frac {4}{8i+1}}-{\frac {2}{8i+4}}-{\frac {1}{8i+5}}-{\frac {1}{8i+6}}\right)

Công thức này, không giống những công thức trước đó, hoàn toàn có thể sinh ra bất kỳ chữ số hệ thập lục phân của π mà không giám sát tới những chữ số đứng trước nó [ 98 ]. Các chữ số nhị phân hay bát phân riêng rẽ hoàn toàn có thể trích xuất từ những chữ số hệ thập lục phân. Các biến thể của thuật toán này đã được phát hiện, nhưng cho tới nay chưa tìm thấy thuật toán trích xuất chữ số nào sinh ra nhanh gọn những chữ số thập phân [ 100 ]. Một ứng dụng quan trọng của những thuật toán trích xuất chữ số là hợp thức hóa những công bố mới về kỉ lục tính toán số π : sau khi một kỉ lục được công bố, những hiệu quả thập phân được chuyển sang hệ thập lục phân, và sau đó một thuật toán trích xuất chữ số được dùng để giám sát 1 số ít ngẫu nhiên những chữ số gần cuối, nếu chúng tương thích, điều này cung ứng một giải pháp đáng tin cậy rằng đo lường và thống kê tổng thể và toàn diện là đúng [ 92 ] .Giữa năm 1998 và 2000, dự án Bất Động Sản giám sát phân bổ PiHex sử dụng công thức Bellard ( một bản chỉnh sửa của thuật toán BBP ) để giám sát bit thứ một triệu tỉ ( 1015 ) của π, đã cho ra tác dụng là 0 [ 101 ]. Tháng Chín năm 2010, một nhân viên cấp dưới của Yahoo ! đã sử dụng ứng dụng Hadoop của công ty trên một ngàn máy tính trong một thời hạn 23 ngày để giám sát 256 bit của π ở vị trí bit 2 triệu tỉ ( 2 × 1015 ) [ 102 ] .
Do π liên hệ ngặt nghèo với đường tròn, nó Open trong nhiều công thức thuộc những nghành hình học và lượng giác, đặc biệt quan trọng là những công thức tương quan tới đường tròn, hình cầu, hoặc elip. Một số ngành khoa học khác cũng có những công thức tương quan tới π, như thống kê, phân dạng, cơ học, ngoài hành tinh học, triết lý số, và điện từ học .

Hình học và lượng giác.

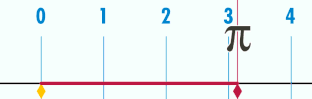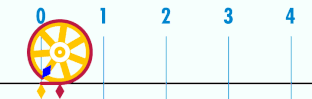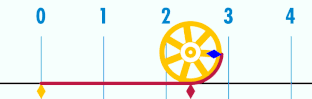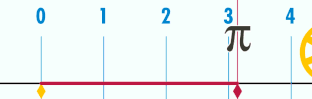π được định nghĩa là tỉ lệ giữa chu vi và đường kính của một đường tròn.được định nghĩa là tỉ lệ giữa chu vi và đường kính của một đường tròn .π Open trong những công thức về chu vi, diện tích quy hoạnh và thể tích những hình hình học tương quan tới đường tròn, như những hình elip, hình cầu, hình nón, hình xuyến. Một vài công thức phổ cập hơn cả trong số đó là [ 103 ] :

Chu vi của một đường tròn với đường kính $d$

Xem thêm: 100 cap về bầu trời, stt về bầu trời hay nhẹ nhàng và ý nghĩa

là $\pi d$
Diện tích của một hình tròn với đường kính $d$
là ${\tfrac {1}{4}}\pi d^{2}$
Chu vi của một đường tròn với bán kính $r$
là $2\pi r$
Diện tích của một hình tròn với bán kính $r$
là $\pi r^{2}$
Thể tích của một hình cầu với bán kính $r$
là ${\tfrac 43}\pi r^{3}$
Diện tích mặt cầu với bán kính $r$
là $4\pi r^{2}$

π Open trong những tích phân xác lập miêu tả chu vi, diện tích quy hoạnh, hoặc thể tích những hình tạo ra từ đường tròn. Chẳng hạn, một tích phân xác lập nửa diện tích quy hoạnh của một đường tròn với nửa đường kính bằng 1 được cho bởi [ 104 ] :

\int _{{-1}}^{1}{\sqrt {1-x^{2}}}\,dx={\frac {\pi }{2}}

Trong công thức này, hàm

1
−

{\displaystyle \scriptstyle {\sqrt {1-x^{2}}}}

$\scriptstyle {\sqrt {1-x^{2}}}$ biểu diễn nửa trên của đường tròn (căn thức là hệ quả của định lý Pythagoras), và tích phân

∫

−
1

{\displaystyle \scriptstyle \int _{-1}^{1}}

$\scriptstyle \int _{{-1}}^{1}$ tính diện tích giữa nửa đường tròn và trục x.

sin và cosin lặp lại với chu kì 2π.Các hàmvàlặp lại với chu kì 2Trong lượng giác, những hàm lượng giác liên hệ với những góc, và những nhà toán học thường sử dụng radian như một đơn vị chức năng đo. Mặt khác, π đóng một vai trò quan trọng trong những góc đo bằng radian, do radian được định nghĩa sao cho một đường tròn chiếm một góc bằng 2 π radian [ 105 ], hoặc nói cách khác, góc 180 ° bằng với π radian, và 1 ° = π / 180 radian [ 105 ] .

Các hàm lượng giác phổ biến thường có chu kì là bội của π; chẳng hạn, sin và cosin có chu kỳ 2π[106], do đó với bất kì góc θ và bất kì số nguyên k nào,

sin
⁡
θ
=
sin
⁡

(

θ
+
2
π
k

)

{\displaystyle \scriptstyle \sin \theta =\sin \left(\theta +2\pi k\right)}

$\scriptstyle \sin \theta =\sin \left(\theta +2\pi k\right)$ và

cos
⁡
θ
=
cos
⁡

(

θ
+
2
π
k

)

{\displaystyle \scriptstyle \cos \theta =\cos \left(\theta +2\pi k\right).}

$\scriptstyle \cos \theta =\cos \left(\theta +2\pi k\right).$ [106]

Phương pháp Monte Carlo.

a và b được thả ngẫu nhiên.Kim Buffon. Các cây kimvàđược thả ngẫu nhiên.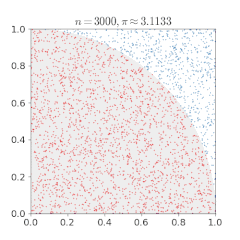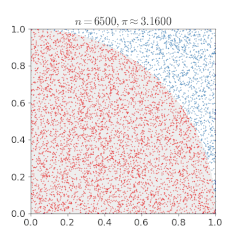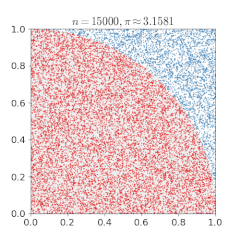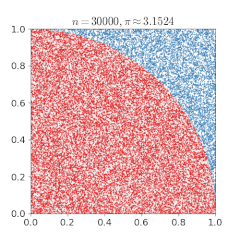Các chấm ngẫu nhiên được đặt trên một hình vuông vắn nội tiếp với nó .π.Phương pháp Monte Carlo, dựa trên phép thử ngẫu nhiên, có thể dùng để ước lượng số

Họ phương pháp Monte Carlo, vốn dùng để tính toán kết quả của những phép thử ngẫu nhiên nhiều lần, có thể dùng để tạo nên các phép xấp xỉ số π[107]. Kim Buffon là một kĩ thuật như vậy: nếu một cây kim có chiều dài ℓ được thả n lần lên một bề mặt trên đó vẽ các đường thẳng song song cách nhau t đơn vị, và nếu x lần trong số đó nó dừng lại cắt qua một vạch (x > 0), thì người ta có thể tính gần đúng π dựa trên phép tính[108]:

\pi \approx {\frac {2n\ell }{xt}}

Một phương pháp Monte Carlo khác để tính π là vẽ một đường tròn nội tiếp một hình vuông, và đặt ngẫu nhiên các chấm lên hình vuông. Tỉ lệ các chấm nằm trong hình tròn trên tổng số chấm xấp xỉ bằng

{\displaystyle \scriptstyle \pi /4.}

$\scriptstyle \pi /4.$ [109]

Phương pháp Monte Carlo để tính gần đúng π rất chậm so với những giải pháp khác. Năm 1901 nhà toán học Italia Mario Lazzarini đã tung một cây kim 3048 lần để thu được hiệu quả ước đạt π bằng 355 / 113 [ 110 ], một thí nghiệm nhằm mục đích minh họa cho giải pháp hơn là nỗ lực lập kỉ lục về số π. Mô phỏng trên máy tính tân tiến được cho phép triển khai ” gieo ” ngẫu nhiên nhanh hơn nhiều cách tung kim bằng tay như vậy, nhưng nhìn chung nó không khi nào được dùng để tính π khi yên cầu độ đúng chuẩn và vận tốc [ 111 ] .

Số phức và giải tích.

Bất kỳ số phức z nào đều có thể biểu diễn bằng một cặp số thực. Trong hệ tọa độ cực, một số (bán kính r) được dùng để biểu diễn khoảng cách từ z tới gốc tọa độ của mặt phẳng phức và một số khác (góc φ) để biểu diễn một phép quay ngược chiều kim đồng hồ từ tia dương của trục thực tới z[112]:

z=r\cdot (\cos \varphi +i\sin \varphi )

Ở đây i2 = −1. Sự xuất hiện thường xuyên của π trong giải tích phức liên quan tới biểu diễn hàm mũ của một biến phức, được mô tả bằng công thức Euler[113]:

e^{{i\varphi }}=\cos \varphi +i\sin \varphi

Ở đây hằng số e là cơ số của lôgarit tự nhiên. Công thức này lập lên một mối liên hệ giữa lũy thừa ảo của e và các điểm trên đường tròn đơn vị có tâm ở gốc của mặt phẳng phức. Đặt φ = π trong công thức Euler sinh ra Đồng nhất thức Euler, một công thức được các nhà toán học ca ngợi do chứa đựng năm hằng số toán học quan trọng nhất[113][114]:

e^{{i\pi }}+1=0

Có n số phức z khác nhau thỏa mãn

=
1

{\displaystyle z^{n}=1}

$z^{n}=1$ , và chúng được gọi là “nghiệm bậc n của đơn vị”[115]. Chúng được cho bởi công thức:

e^{{2\pi ik/n}}\qquad (k=0,1,2,\dots ,n-1)

Công thức tích phân Cauchy chi phối những hàm giải tích phức và thiết lập mối quan hệ quan trọng giữa những phép tích phân và vi phân, gồm có một điều đáng quan tâm là giá trị của một hàm phức trong một miền đóng hoàn toán được xác lập bởi những giá trị trong miền [ 116 ] [ 117 ] :

f(z_{{0}})={\frac {1}{2\pi i}}\oint _{\gamma }{f(z) \over z-z_{0}}\,dz

π có thể tính được từ hoàn toàn có thể tính được từ tập Mandelbrot, bằng cách tính số vòng lặp thiết yếu trước khi điểm ( − 0.75, ε ) phân kỳ .Sự hiện hữu của π trong fractal ( phân dạng ) tập Mandelbrot được một người Mỹ tên là David Boll mày mò vào năm 1991 [ 118 ]. Ông đã kiểm tra bộc lộ của tập Mandelbrot ở gần vùng ” cổ ” ở ( – 0.75, 0 ). Xem xét những điểm có tọa độ ( – 0.75, ε ), khi ε tiến tới 0, số lần tự lặp lại hình dạng của tập cho đến khi phân kì so với điểm đó nhân với ε quy tụ về π. Điểm ( 0.25, ε ) ở đỉnh của một ” thung lũng ” lớn ở phía phải của tập Mandelbrot cũng biểu lộ tương tự như : số lần tự tái diễn trước khi phân kì nhân với căn bậc hai của ε tiến tới π [ 118 ] [ 119 ] .

Hàm gamma mở rộng khái niệm về giai thừa – vốn thông thường chỉ được định nghĩa cho các số nguyên – sang mọi số thực. Nếu hàm gamma được tính ở các số bán nguyên, thì kết quả sẽ chứa π, chẳng hạn

Γ
(
1

2
)
=

{\displaystyle \scriptstyle \Gamma (1/2)={\sqrt {\pi }}}

$\scriptstyle \Gamma (1/2)={\sqrt {\pi }}$ và

Γ
(
5

2
)
=

{\displaystyle \scriptstyle \Gamma (5/2)={\frac {3{\sqrt {\pi }}}{4}}}

$\scriptstyle \Gamma (5/2)={\frac {3{\sqrt {\pi }}}{4}}$ [120]. Hàm gamma có thể được sử dụng để tạo ra một phép tính gần đúng

n
!

{\displaystyle \scriptstyle n!}

$\scriptstyle n!$ cho số

{\displaystyle \scriptstyle n}

$\scriptstyle n$ lớn:

n
!
∼

2
π
n

(

n
e

)

{\displaystyle \scriptstyle n!\sim {\sqrt {2\pi n}}\left({\frac {n}{e}}\right)^{n}}

$\scriptstyle n!\sim {\sqrt {2\pi n}}\left({\frac {n}{e}}\right)^{n}$ còn được gọi là xấp xỉ Stirling[121].

Giá trị riêng.

Trong nhiều ứng dụng, số pi đóng vai trò đặc biệt là một giá trị riêng. Ví dụ, một sợi dây rung có thể được mô hình hóa bằng đồ thị của một hàm số f trên đoạn đơn vị [0,1], với hai đầu cố định f(0) = f(1) = 0. Các chế độ (hàm) rung động của dây là nghiệm của một phương trình vi phân,

f
″

(
x
)
+
λ
f
(
x
)
=
0

{\displaystyle f”(x)+\lambda f(x)=0}

$f''(x)+\lambda f(x)=0$ hay

f
″

(
t
)
=
−
λ
f
(
x
)

{\displaystyle f”(t)=-\lambda f(x)}

$f''(t)=-\lambda f(x)$ . Vì thế λ là một giá trị riêng của toán tử đạo hàm cấp hai

f
↦

f
″

{\displaystyle f\mapsto f”}

$f\mapsto f''$ , và bị ràng buộc theo lý thuyết Sturm–Liouville, nó chỉ có ở một vài giá trị nhất định. Nó phải là số dương vì toán tử là xác định âm, vậy ta có thể viết λ = ν2, trong đó số ν > 0 được gọi số sóng. Vì vậy f(x) = sin(π x) thỏa mãn điều kiện biên và phương trình vi phân, với ν = π.[122]

Giá trị của π thực ra là giá trị nhỏ nhất của số sóng, và nó tương ứng với chế độ cơ bản của sợi dây rung. Một cách để cho thấy điều này là ước tính năng lượng, thỏa mãn bất đẳng thức Wirtinger:[123] đối với một hàm f : [0, 1] → ℂ với f(0) = f(1) = 0; f và f ‘ đều khả tích bình phương, ta có:

\pi ^{2}\int _{0}^{1}|f(x)|^{2}\,dx\leq \int _{0}^{1}|f'(x)|^{2}\,dx,

với đẳng thức xảy ra chỉ khi f là một bội của sin(π x). Ở đây π là một hằng số tối ưu trong bất đẳng thức Wirtinger, và có thể suy ra rằng nó là số sóng nhỏ nhất, sử dụng đặc trưng biến thiên của giá trị riêng. Hệ quả là, π là giá trị suy biến nhỏ nhất của toán tử đạo hàm trên không gian các hàm số trên đoạn [0,1] mà bằng 0 tại các điểm đầu mút (không gian Sobolev

[
0
,
1
]

{\displaystyle H_{0}^{1}[0,1]}

$H_{0}^{1}[0,1]$ ).

Lý thuyết số và hàm zeta Riemann.

Hàm zeta Riemann ζ(s) được dùng trong nhiều lĩnh vực của toán học. Khi tính cho

s
=
2

{\displaystyle \scriptstyle s=2}

$\scriptstyle s=2$ , nó có thể viết lại thành

\zeta (2)={\frac {1}{1^{2}}}+{\frac {1}{2^{2}}}+{\frac {1}{3^{2}}}+\cdots

Tìm một nghiệm đơn cho chuỗi vô hạn này là một bài toán nổi tiếng trong toán học gọi là bài toán Basel. Leonhard Euler giải nó vào năm 1735 khi ông chỉ ra nó bằng

{\displaystyle \scriptstyle {\frac {\pi ^{2}}{6}}}

$\scriptstyle {\frac {\pi ^{2}}{6}}$ [67]. Kết quả của Euler dẫn đến một kết luận quan trọng trong lý thuyết số là xác suất để hai số ngẫu nhiên nguyên tố cùng nhau (nghĩa là không có ước chung nào ngoài 1) bằng

{\displaystyle \scriptstyle 6/\pi ^{2}}

$\scriptstyle 6/\pi ^{2}$ .[124][125]. Xác suất này dựa trên một nhận xét rằng bất kì số nào chia hết cho một số nguyên tố

{\displaystyle \scriptstyle p}

$\scriptstyle p$ là

{\displaystyle \scriptstyle 1/p}

$\scriptstyle 1/p$ (chẳng hạn, cứ bảy số nguyên liên tiếp thì có một số chia hết cho 7). Do đó xác suất để hai số cùng chia hết bởi số nguyên tố này là

{\displaystyle \scriptstyle 1/p^{2}}

$\scriptstyle 1/p^{2}$ , và xác suất để ít nhất một trong hai số không chia hết là

1
−
1

{\displaystyle \scriptstyle 1-1/p^{2}}

$\scriptstyle 1-1/p^{2}$ . Đối với các số nguyên khác nhau, các sự kiện có thể chia hết là độc lập với nhau; do đó xác suất để hai số nguyên tố cùng nhau cho bởi một tích lấy trên tất cả các số nguyên tố[126]:

\prod _{p}^{{\infty }}\left(1-{\frac {1}{p^{2}}}\right)=\left(\prod _{p}^{{\infty }}{\frac {1}{1-p^{{-2}}}}\right)^{{-1}}={\frac {1}{1+{\frac {1}{2^{2}}}+{\frac {1}{3^{2}}}+\cdots }}={\frac {1}{\zeta (2)}}={\frac {6}{\pi ^{2}}}\approx 61\%

Xác suất này hoàn toàn có thể dùng cùng với một giải pháp sinh số ngẫu nhiên để tính gần đúng π sử dụng cách tiếp cận Monte Carlo [ 127 ] .

Mặc dù không phải là một hằng số vật lý, π xuất hiện thường xuyên trong các phương trình mô tả các nguyên lý cơ bản của vũ trụ, thường do mối liên hệ giữa π với đường tròn và với hệ tọa độ cầu. Một công thức đơn giản trong lĩnh vực cơ học cổ điển cho ta chu kỳ dao động gần đúng T của một con lắc đơn với chiều dài L, dao động với biên độ nhỏ (g là gia tốc trọng trường trên bề mặt Trái Đất)[128]:

T\approx 2\pi {\sqrt {\frac {L}{g}}}

Một trong những công thức tối quan trọng của cơ học lượng tử là nguyên lý bất định Heisenberg chỉ ra rằng độ bất định trong phép đo vị trí của một hạt (Δx) và động lượng (Δp) không thể đồng thời nhỏ tùy ý ở cùng một thời điểm (ở đây h là hằng số Planck)[129]:

\Delta x\,\Delta p\geq {\frac {h}{4\pi }}

Trong ngành thiên hà học, π Open trong một công thức nền tảng, đó là phương trình trường Einstein tạo nên cơ sở của thuyết tương đối tổng quát và diễn đạt tương tác cơ bản của lực mê hoặc như một hiệu quả của không-thời gian bị uốn cong bởi vật chất và nguồn năng lượng [ 130 ] :

Trong lĩnh vực điện từ học, định luật Coulomb mô tả điện trường giữa hai điện tích (q1 và q2) cách nhau một khoảng r (với ε0 biểu diễn cho hằng số điện môi trong chân không)[131]:

F={\frac {\left|q_{1}q_{2}\right|}{4\pi \varepsilon _{0}r^{2}}}

Việc π xấp xỉ bằng 3 góp phần vào thời gian sống tương đối lâu của ortho-positronium (hệ lượng tử có một electron và một positron nằm trên cùng một quỹ đạo quay xung quanh một khối tâm). Nghịch đảo thời gian sống

1
τ

{\displaystyle {\frac {1}{\tau }}}

${\frac {1}{\tau }}$ đối với bậc thấp nhất trong hằng số cấu trúc tế vi

{\displaystyle \alpha }

$\alpha$ được cho bởi công thức[132]:

{\frac {1}{\tau }}=2{\frac {\pi ^{2}-9}{9\pi }}m\alpha ^{{6}}

trong đó m là khối lượng electron.

Xác suất thống kê.

ƒ(x) = e−x2. Vùng tô màu giữa hàm số và trục x có diện tích $\scriptstyle {\sqrt {\pi }}$ Một đồ thị Hàm Gauss ) =. Vùng tô màu giữa hàm số và trụccó diện tích quy hoạnhCác nghành nghề dịch vụ Xác Suất và thống kê sử dụng liên tục phân bổ chuẩn như một quy mô đơn thuần cho những hiện tượng kỳ lạ phức tạp ; ví dụ điển hình những nhà khoa học thường thì giả định rằng những sai số quan sát trong hầu hết những thí nghiệm tuân theo một phân bổ chuẩn [ 133 ]. π được tìm thấy trong hàm Gauss ( là hàm tỷ lệ Tỷ Lệ của phân bổ chuẩn với giá trị trung bình μ và độ lệch chuẩn σ [ 134 ] :

f(x)={1 \over \sigma {\sqrt {2\pi }}}\,e^{{-(x-\mu )^{2}/(2\sigma ^{2})}}

Diện tích dưới đồ thị của đường cong phân bổ chuẩn được cho bởi tích phân Gauss [ 134 ] :

\int _{{-\infty }}^{\infty }e^{{-x^{2}}}\,dx={\sqrt {\pi }}

trong khi tích phân tương tự như so với phân bổ Cauchy là

\int _{{-\infty }}^{{\infty }}{\frac {1}{x^{2}+1}}\,dx=\pi

Kỹ thuật và địa chất.

π hiện diện trong một số công thức trong kĩ thuật cấu trúc, như công thức tính độ cong vênh do Euler tìm ra, cho ta biết tải trọng theo trục tối đa F mà một cột dài, mảnh có độ dài L, suất đàn hồi E, và momen quán tính diện tích I có thể mang được mà không bị cong vênh[135]:

F={\frac {\pi ^{2}EI}{L^{2}}}

Lĩnh vực thủy động lực học cũng chứa π trong định luật Stokes, cho phép tính gần đúng lực ma sát F tác dụng lên một vật thể nhỏ dạng cầu bán kính R chuyển động với vận tốc v trong một chất lỏng với độ nhớt động η[136]:

F=6\,\pi \,\eta \,R\,v

Biến đổi Fourier là một phép toán màn biểu diễn thời hạn như một hàm của tần số, được biết như phổ tần số của nó. Nó có nhiều ứng dụng trong vật lý và kỹ thuật, đặc biệt quan trọng trong giải quyết và xử lý tín hiệu [ 137 ] :

{\hat {f}}(\xi )=\int _{{-\infty }}^{{\infty }}f(x)\ e^{{-2\pi ix\xi }}\,dx

Dưới những điều kiện kèm theo lý tưởng ( dốc thoải đều trên một nền xói mòn một cách đồng đều ), độ uốn khúc của một con sông tiến gần tới π. Độ uốn khúc ( sinousity ) là tỉ số giữa độ dài thực và khoảng cách theo đường kẻ giữa thượng nguồn và cửa sông. Các dòng chảy nhanh hơn dọc những cạnh bên ngoài của chỗ uốn dòng sông gây ra nhiều xói lở hơn dọc những cạnh trong, do đó đẩy những chỗ uốn ra xa hơn, và ngày càng tăng sự uốn vòng lặp lại toàn diện và tổng thể của dòng sông. Tuy nhiên, sự uốn vòng quá mức dẫn tới ở một số ít chỗ, dòng cuộn thành một đường vòng quanh, tạo ra những hồ có hình chữ U ( box-ow lake ), làm giảm độ uốn khúc tổng thể và toàn diện. Sự cân đối giữa hai tác nhân trái chiều này khiến cho dẫn tới độ uốn khúc của dòng sông trung bình gần bằng π [ 138 ] [ 139 ] .

Ngoài khoa học.

Ghi nhớ những chữ số.

Nhiều người đã cố gắng nhớ càng nhiều càng tốt các chữ số của π, một sự luyện tập được gọi là piphilology (kết hợp từ pi và philology tức ngữ văn học)[140]. Một kĩ thuật phổ biến là ghi nhớ một câu chuyện hay một bài thơ, trong đó độ dài các từ ứng với số các chữ số: từ thứ nhất có 3 chữ cái, từ thứ hai có 1, từ thứ ba có 4, thứ tư có 1, thứ năm có 4, và tiếp tục như vậy. Một trong những ví dụ sớm nhất về biện pháp hỗ trợ ghi nhớ này được đề xuất bởi nhà khoa học Anh James Hopwood Jeans: “How I want a drink, alcoholic of course, after the heavy lectures involving quantum mechanics” (tạm dịch: Tất nhiên là tôi muốn một ly đồ uống, đồ uống có cồn, sau những bài giảng nặng nề liên quan đến cơ học lượng tử)[140]. Một bài thơ (tiếng Anh: poem) dùng cho việc ghi nhớ này đôi khi được gọi là một piem. Ngoài tiếng Anh, các bài thơ để ghi nhớ π cũng được sáng tác trong một số ngôn ngữ khác[140].

Kỉ lục về ghi nhớ những chữ số của π, được xác nhận bởi Sách Kỷ lục Guinness, là 67 890 chữ số, được Lữ Siêu, một người Trung Quốc đọc thuộc lòng trong 24 giờ và 4 phút vào ngày 20 tháng 11 năm 2005 [ 141 ] [ 142 ]. Năm 2006, một kĩ sư Nhật Bản về hưu tên là Haraguchi Akira công bố là đã đọc thuộc lòng 100 000 chữ số, nhưng công bố này không được sách Kỷ lục Guinness kiểm chứng [ 143 ]. Những người lập nên kỉ lục về ghi nhớ những chữ số của π thường không dựa vào những bài thơ, mà sử dụng những giải pháp khác, như nhớ những khuôn dạng số hay chiêu thức loci ( ghi nhớ bằng cách liên hệ số với vị trí ) [ 144 ] .

Một vài tác giả sử dụng các chữ số của π để thiết lập nên một dạng hạn từ mới, trong đó độ dài từ yêu cầu phải biểu diễn các chữ số của π, trong tiếng Anh gọi là pilish. Truyện thơ ngắn Cadaeic Cadenza chứa 3835 chữ số đầu tiên của π theo cách này[145], và toàn bộ cuốn sách Not a Wake chứa 10 000 từ, mỗi từ biểu diễn một chữ số của π[146].

Trong văn hóa truyền thống đại chúng.

Pi Pie)Bánh Pi ( tiếng Anh :Có lẽ do π có định nghĩa đơn thuần mà lại hiện hữu ở khắp những nghành nghề dịch vụ, nó được biểu lộ trong văn hóa truyền thống đại chúng nhiều hơn bất kể khái niệm toán học nào khác. Tại kho lưu trữ bảo tàng Palais de la Découverte ở Paris có một căn phòng hình tròn trụ được gọi là ” phòng pi ” trên tường bộc lộ 707 vần âm của π, dưới dạng những ký tự làm bằng gỗ gắn vào trần vòm. Các chữ số này dựa trên giám sát năm 1853 của William Shanks có chứa một lỗi sai mở màn từ chữ số thứ 528. Lỗi này được phát hiện năm 1946 và được sửa lại vào năm 1949 [ 147 ]
e to the u, du / dx

e to the x, dx

Cosine, secant, tangent, sine

3.14159

Integral, radical, mu dv

Slipstick, slide rule, MIT!

GOOOOOO TECH!Lời cổ vũ của trường MIT [ 148 ]
Nhiều trường học ở nước Mỹ cử hành kỉ niệm Ngày số pi vào 14 tháng 3 ( trong ngôn từ Anh-Mỹ, ngày này viết là 3/14 ) [ 149 ]. Ngày 9 tháng 3 năm 2009, Hạ viện Hoa Kỳ đã chính thức chọn ngày 14 tháng 3 hàng năm là ngày số Pi nhằm mục đích khuyến khích học viên, giáo viên nghiên cứu và điều tra toán học. [ 150 ] π và chuỗi chữ số của nó thường được những người tự xem mình là ” lập dị ” sử dụng trong những trò đùa của nhóm những người ưa thích toán học và công nghệ tiên tiến. Một vài lời cổ vũ ( trong tranh tài thể thao, văn nghệ … ) của Học viện Công nghệ Massachusetts ( MIT ) cũng Open số ” 3,14159 ” [ 148 ]. Trong vụ bán đấu giá những tài liệu về bằng ý tưởng công nghệ tiên tiến có giá trị của tập đoàn lớn Nortel năm 2010, Google đã liên tục đặt giá một cách khác thường dựa trên những hằng số toán học và khoa học, gồm có π [ 151 ] .

Những người ủng hộ một hằng số toán học mới là tau (τ), bằng 2 lần π, lập luận rằng một hằng số dựa trên tỉ số giữa chu vi đường tròn với bán kính của nó thay vì với đường kính sẽ có tính tự nhiên hơn và sẽ đơn giản hóa nhiều công thức[152][153]. Trong khi những đề xuất của họ, như việc tổ chức kỉ niệm ngày 28 tháng 6 như “Ngày Tau” được tường thuật trên truyền thông, họ không được các sách vở khoa học phản ánh[154][155].

Trong tiểu thuyết “Contact”, Carl Sagan đề xuất rằng Đấng Sáng tạo ra vũ trụ đã chôn giấu một thông điệp ẩn sâu trong các chữ số của π[156]. Các chữ số của π cũng được đưa vào lời ca của bài hát “Pi” trong album Aerial của Kate Bush[157]. Pi cũng được dùng để đặt tên cho một bài hát trong album “Horses and Grasses” phát hành năm 2005 của ban nhạc Mỹ Hard ‘n Phirm.[158][159]

Năm 1897, nhà toán học nghiệp dư Edwin J. Goodwin đã nỗ lực thuyết phục cơ quan lập pháp bang Indiana (Hoa Kỳ) thông qua Dự luật Indiana Pi, trong đó mô tả một phương pháp cầu phương hình tròn, và chứa những nội dung giả thiết những giá trị sai của π như 3,2.[160] Dự luật này nổi danh như một nỗ lực thiết lập một chân lý khoa học bằng sắc lệnh lập pháp. Dự thảo đã được Hạ nghị viện Indiana thông qua, nhưng bị Thượng nghị viện bác bỏ[161].

Trong tập Midnight thuộc sêri Doctor Who, vị Tiến sĩ chạm trán với Thực thể Nửa đêm (Midnight Entity), kẻ nhập xác một số nhân vật. Nhân vật Sky Silvestry khi bị nhập xác đã bắt chước kiểu nói của Tiến sĩ bằng cách lặp lại khớp nhau số π tới 30 chữ số thập phân[162]. Điều này đòi hỏi các diễn viên David Tennant và Leslie Sharp học chuỗi số để có thể nhắc lại nó.

Tiểu thuyết của Yann Martel xuất bản năm 2001, [ 163 ] được dựng thành phim năm 2012 [ 164 ] ( Lý An đạo diễn ) nói về nhân vật chính tên Pi hoàn toàn có thể nhớ được rất nhiều chữ số thập phân của Pi .Trong Thuyền trưởng Đơn Vị, một tác phẩm của nhà văn Liên Xô Vladimir Lyovshin, Pi là một nhân vật cùng đi với Số Không, thuyền trưởng Đơn Vị và Hoa Tiêu trong cuộc hải trình .