Hình thoi là gì?

Hình thoi là tứ giác có bốn cạnh bằng nhau. Đây là hình bình hành có hai cạnh kề bằng nhau hay hình bình hành có hai đường chéo vuông góc với nhau .

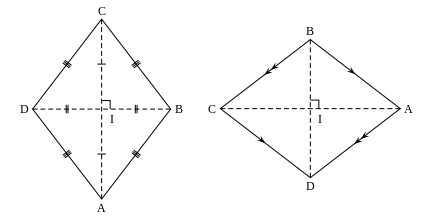
Tính chất của hình thoi

Trong một hình thoi có:

• Các góc đối nhau bằng nhau.
• Hai đường chéo vuông góc với nhau và cắt nhau tại trung điểm của mỗi đường.
• Hai đường chéo là các đường phân giác của các góc của hình thoi.
• Hình thoi có tất cả tính chất của hình bình hành.

Dấu hiệu nhận biết hình thoi

Hình tứ giác đặc biệt

• Tứ giác có bốn cạnh bằng nhau là hình thoi.
• Tứ giác có 2 đường chéo là đường trung trực của nhau là hình thoi.
• Tứ giác có 2 đường chéo là đường phân giác của cả bốn góc là hình thoi.

Hình bình hành đặc biệt

Hình thoi là một dạng đặc biệt quan trọng của một hình bình hành vì nó có không thiếu đặc thù của hình bình hành và còn có một số ít đặc thù khác :

• Hình bình hành có hai cạnh kề bằng nhau là hình thoi.
• Hình bình hành có hai đường chéo vuông góc với nhau là hình thoi.
• Hình bình hành có một đường chéo là đường phân giác của một góc là hình thoi.

Tham khảo thêm:

Cách chứng minh hình thoi

Để chứng tỏ một tứ giác hoặc một hình bình hành là hình thoi, tất cả chúng ta sẽ dựa vào những tín hiệu nhận ra hình thoi như đã nêu ở trên .

Cách 1: Tứ giác có bốn cạnh bằng nhau

Ví dụ : Chứng minh rằng những trung điểm của bốn cạnh của một hình chữ nhật là những đỉnh của hình thoi .

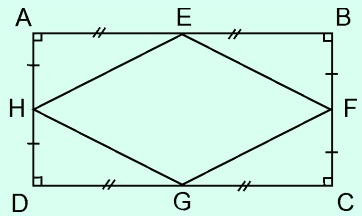
Xét tam giác ABD có E và H lần lượt là trung điểm của AB và AD
⇒ EH là đường trung bình của tam giác
⇒ EH = ½ BD ( 1 )
Chứng minh tương tự như ta có : EF = 1/2 AC ; FG = 1/2 BD ; HG = 1/2 AC ( 2 )
Vì ABCD là hình chữ nhật nên AC = BD ( 3 )
Từ ( 1 ), ( 2 ) và ( 3 ), ta suy ra EH = EF = HG = GF
⇒ Tứ giác EFGH là hình thoi do có bốn cạnh bằng nhau .

Cách 2: Tứ giác có 2 đường chéo là đường trung trực của nhau

Ví dụ : Cho hình bình hành ABCD có AB = AC. Kéo dài trung tuyến AM của ΔABC và lấy ME = MA. Chứng minh tư giác ABEC là hình thoi .

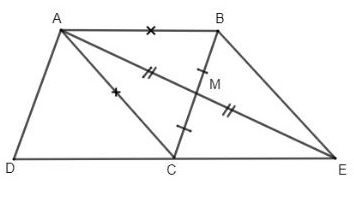
Lời giải :
Theo bài ra, ta có :
ΔABC cân tại A có trung tuyến AM
⇒ AM đồng thời là đường trung trực của BC
⇒ Tứ giác ABEC là hình thoi do có 2 đường chéo là đường trung trực của nhau .

Cách 3: Hình bình hành có hai cạnh kề bằng nhau

Ví dụ : Cho tam giác ABC, lấy những điểm D, E theo thứ tự trên những cạnh AB, AC sao cho BD = CE. Gọi M, N, I, K lần lượt là trung điểm của BE, CD, DE, BC. Chứng minh rằng : IMNK là hình thoi .

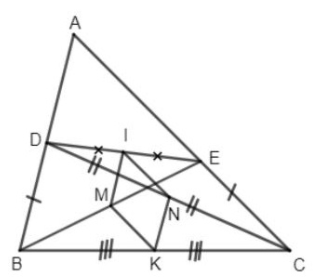
Lời giải
Theo giả thiết ta có : M là trung điểm của BE và I là trung điểm của DE
⇒ MI là đường trung bình của ΔBDE
⇒ MI / / BD và MI = ½ BD
Chứng minh tựa như, ta có :
NK / / BD và NK = ½ BD
Do có MI / / NK và MI = NK nên tứ giác MINK là hình bình hành ( 4 )
Chứng minh tựa như, ta có : IN là đường trung bình của ΔCDE
⇒ IN = ½ CE mà CE = BD ( gt ) => IN = IM ( 5 )
Từ ( 4 ) và ( 5 ) => Tứ giác MINK là hình thoi do là hình bình hành có hai cạnh kề bằng nhau .

Cách 4: Hình bình hành có hai đường chéo vuông góc

Ví dụ : Gọi O là giao điểm hai đường chéo của hình bình hành ABCD. Chứng minh rằng giao điểm những đường phân giác trong của những tam giác AOB ; BOC ; COD và DOA là đỉnh của một hình thoi .

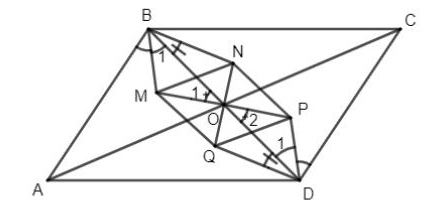
Lời giải
Gọi M, N, P., Q. lần lượt là giao điểm những phân giác trong của những tam giác AOB, BOC, COD và DOA .
Do O là giao điểm hai đường chéo AC và BD của hình bình hành ABCD nên OA = OC và OB = OD .
Xét ΔBMO và ΔDPO có :
Góc B1 = D1 và Góc O1 = O1 ( đối đỉnh ) và OB = OD ( gt )
⇒ ΔBMO = ΔDPO ( g. c. g )
⇒ OM = OP và những điểm M, O, P. thẳng hàng ( 6 )
Chứng minh tựa như : ON = OQ và N, O, P. thẳng hàng ( 7 )
Từ ( 6 ) và ( 7 ) Suy ra : Tứ giác MNPQ là hình bình hành do những đường chéo cắt nhau tại trung điểm mỗi đường. ( 8 )
Mặt khác OM, ON là hai đường phân giác của hai góc kề bù nên OM ⊥ ON. ( 9 )
Từ ( 8 ) và ( 9 ) suy ra : MNPQ là hình thoi do là hình bình hành có hai đường chéo vuông góc .

Bài tập về hình thoi

Ví dụ 1 : Trong những hình sau, hình nào là hình thoi ? Vì sao ?

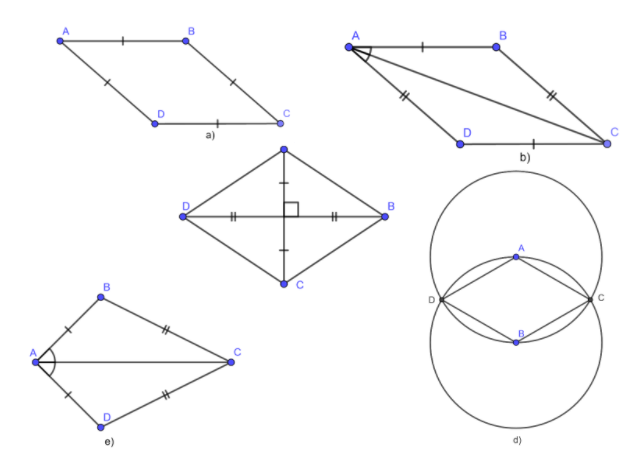
Lời giải

a) Tứ giác ABCD có AB = BC = CD = DA nên ABCD là hình thoi

b ) Tứ giác ABCD có AB = CD, AD = BC nên ABCD là hình bình hành .
Hình bình hành ABCD có đường chéo AC là đường phân giác góc A ∧ nên ABCD là hình thoi .
c ) Tứ giác ABCD có hai đường chéo AC và BD vuông góc với nhau tại trung điểm của mỗi đường nên ABCD là hình thoi
d ) Ta có : B, C, D đều thuộc đường tròn tâm A nên AB = AC = AD ( 1 )
A, C, D đều thuộc đường tròn tâm B nên AB = BC = BD ( 2 )
Từ ( 1 ) và ( 2 ) suy ra, AC = AD = BC = BD
Do đó, ABCD là hình thoi .
e ) Tứ giác ABCD có những cạnh đối lập không bằng nhau, do đó ABCD không là hình thoi .
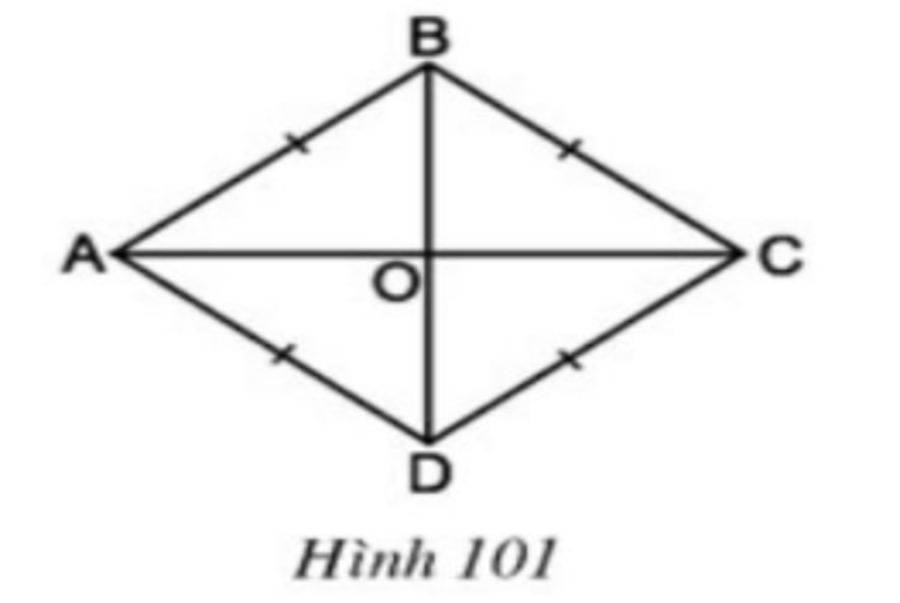
Ví dụ 2 : Cho hình thoi ABCD, hai đường chéo cắt nhau tại O ( h. 101 ) .
a ) Theo đặc thù của hình bình hành, hai đường chéo của hình thoi có đặc thù gì ?
b ) Hãy phát hiện thêm những đặc thù khác của hai đường chéo AC và BD .

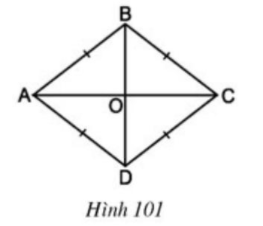
Lời giải
a ) Theo đặc thù của hình bình hành, hai đường chéo của hình thoi có đặc thù cắt nhau tại trung điểm mỗi đường
b ) Xét ΔAOB và ΔCOB
AB = CB
BO chung
OA = OC ( O là trung điểm AC )
⇒ ΔAOB = ΔCOB ( c. c. c )
⇒ ( AOB ) = ( COB ), ( ABO ) = ( CBO ) ( những cặp góc tương ứng )
( ABO ) = ( CBO ) ⇒ BO là phân giác góc ABC
( AOB ) + ( COB ) = 180 o ⇒ ( AOB ) = ( COB ) = 180 o : 2 = 90 o
Chứng minh tựa như, ta Tóm lại được :
AC, BD là những đường phân giác của những góc của hình thang
và AC ⊥ BD tại O
Ví dụ 3 : Chứng minh rằng những trung điểm của bốn cạnh của một hình thoi là những đỉnh của một hình chữ nhật .

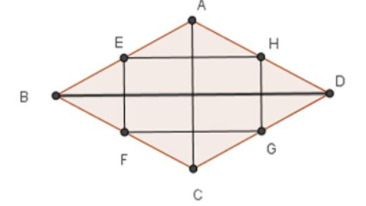
Lời giải
a có : EB = EA, FB = FA ( gt )
Nên EF là đường trung bình của ΔABC .
Do đó EF / / AC
HD = HA, GD = GC ( gt ) nên HG là đường trung bình của ΔADC .
Do đó HG / / AC
Suy ra EF / / HG ( 1 )
Chứng minh tựa như EH / / FG ( 2 )
Từ ( 1 ) và ( 2 ) ta được EFGH là hình bình hành
Lại có : EF / / AC và BD ⊥ AC nên BD ⊥ EF
EH / / BD và EF ⊥ BD nên EF ⊥ EH
Nên góc FEH = 900
Hình bình hành EFGH có E ∧ = 900 nên là hình chữ nhật
Hi vọng đọc xong bài viết của chúng tôi những bạn hoàn toàn có thể nắm được hình thoi là gì ? Tính chất hình thoi và tín hiệu nhận ra hình thoi để vận dụng vào làm bài tập nhé

Đánh giá bài viết

Source: http://139.180.218.5
Category: tản mạn