Bạn đang quan tâm đến Tung độ gốc là gì phải không? Nào hãy cùng SAIGONCANTHO theo dõi bài viết này ngay sau đây nhé, vì nó vô cùng thú vị và hay đấy!
Bài viết sẽ cho biết thông số góc của một đường thẳng là gì cũng như những ví dụ thực tiễn tương quan đến khái niệm tưởng chừng đơn thuần này. Bạn đang xem : Hệ số góc là gì
Đây cũng là phần giúp bạn biết thêm về thông số góc để hoàn toàn có thể hiểu rõ hơn những chủ đề sau tương quan đến nó. Ví dụ như chủ đề vềtiếp tuyến của đồ thị hàm số và đạo hàm bậc nhất của hàm số đó tại một điểm .
Bạn đang xem: Tung độ gốc là gì
Bạn đang đọc: Tung độ gốc là gì
Bạn đang xem: Tung độ gốc là gì
Nội dung chính
Định nghĩa
Tên và cách định nghĩa thông số góc của đường thẳng dựa trên góc tạo bởi đường thẳng đó với trục hoành USD Ox USD 1 .
Định nghĩa 1 ( Hệ số góc của đường thẳng )
Hệ số góc của đường thẳng USD y = ax + b USD với USD a ne 0 $ là thông số của góc tạo thành khi đường thẳng cắt trục hoành USD x’Ox USD tại một điểm và hợp với trục hoành $ x’Ox $ tạo thành một góc. Vì $ a $ trong phương trình hàm số có tương quan đến góc này nên USD a USD được gọi là thông số góc của đường thẳng USD y = ax + b USD .
Khi USD a > 0 $ thì góc tạo thành là góc nhọn và nằm bên trái trục tung USD Oy USD. Khi USD aKhi USD a = 0 $ ta không có thông số góc vì lúc này, đường thẳng song song với trục hoành .
Tuy nhiên, như tôi đã đề cập trong bài viết Hiểu về dấu trừ và phép trừ trong Toán học, đừng nên tin quá nhiều vào tên gọi! Hệ số góc của đường thẳng trong tiếng Anh làThe slope of the line, dịch sát nghĩa tiếng Việt thì nó có nghĩa là “độ dốc/nghiêng của đường thẳng” và được định nghĩa Toán học như sau2.
Định nghĩa 2 ( Hệ số góc của đường thẳng )
Đường thẳng không song song với trục tung có thông số góc ( slope ) miêu tả độ dốc của đường thẳng và được định nghĩa là tỷ suất sự đổi khác theo USD y $ so với sự đổi khác theo USD x USD của hai điểm bất kể nằm trên đường thẳng .
Xem thêm : Eus Là Gì, Bài Giảng Eus
Nếu đường thẳng qua hai điểm USD ( x_1, y_1 ) USD và USD ( x_2, y_2 ) USD thì thông số góc của đường thẳng được tính bằng công thức ( USD x_1 ne x_2 USD )
USD $ a = dfrac { Delta y } { Delta x } = dfrac { y_2-y_1 } { x_2-x_1 }. $ $
Tên gọi của hệ số góc ở mỗi thứ tiếng phụ thuộc nhiều vào định nghĩa tương ứng. Tiếng Việt dùng hệ số góc vì định nghĩa dựa vào góc của đường thẳng và trục hoành. Còn tiếng Anh dùng độ dốc vì định nghĩa dựa vào độ dốc của đường thẳng. Tuy nhiên cả hai định nghĩa này đều cùng nói về một thứ, đó chính là hệ số $a$ trong phương trình đường thẳng $y=ax+b$. Thật vậy, gọi đường thẳng này là (d). Trên (d), ta lấy hai điểm $(x_1,ax_1+b)$ và $(x_2,ax_2+b)$ thì khi đó tỷ số giữa sự chênh lệch theo $y$ so với sự chênh lệch theo $x$ theo như định nghĩa 2 sẽ là
USD USD dfrac { ( ax_2 + b ) – ( ax_1 + b ) } { x_2-x_1 } = dfrac { a ( x_2-x_1 ) } { x_2-x_1 } = a. $ $
Đây cũng chính là thông số USD a $ trong định nghĩa 1 .
Hiểu định nghĩa như thế nào?
Hệ số góc cho ta biết sự nhanh/chậm của sự thay đổi theo $y$ so với sự thay đổi theo $x$ giữa các điểm trên đường thẳng đó. Hay nói cách khác, từ một điểm xuất phát trên đường thẳng, giả sử điểm này có hoành độ là $x_1$, nếu ta thêm hoặc bớt vào $x_1$ một lượng $h$ thì dựa vào độ lớn của hệ số góc $a$, ta sẽ biết được rằng giá trị tương ứng của $y$ khi ấy sẽ thay đổi ít hay nhiều so với $y_1$ ban đầu. Xem hình minh họa bên dưới.
 Nếu USD a > 0 $, ta hiểu rằng USD x USD tăng thì USD y $ chắc như đinh cũng sẽ tăng theo. Còn tăng ít hay nhiều thì còn tùy thuộc vào độ lớn của USD a USD. Ngược lại nếu USD aCòn nếu USD a = 0 USD, rõ ràng khi ấy ( d ) là đường thẳng song song với trục hoành và sự biến hóa của USD x USD sẽ không ảnh hưởng tác động đến sự biến hóa của USD y $ .
Nếu USD a > 0 $, ta hiểu rằng USD x USD tăng thì USD y $ chắc như đinh cũng sẽ tăng theo. Còn tăng ít hay nhiều thì còn tùy thuộc vào độ lớn của USD a USD. Ngược lại nếu USD aCòn nếu USD a = 0 USD, rõ ràng khi ấy ( d ) là đường thẳng song song với trục hoành và sự biến hóa của USD x USD sẽ không ảnh hưởng tác động đến sự biến hóa của USD y $ .


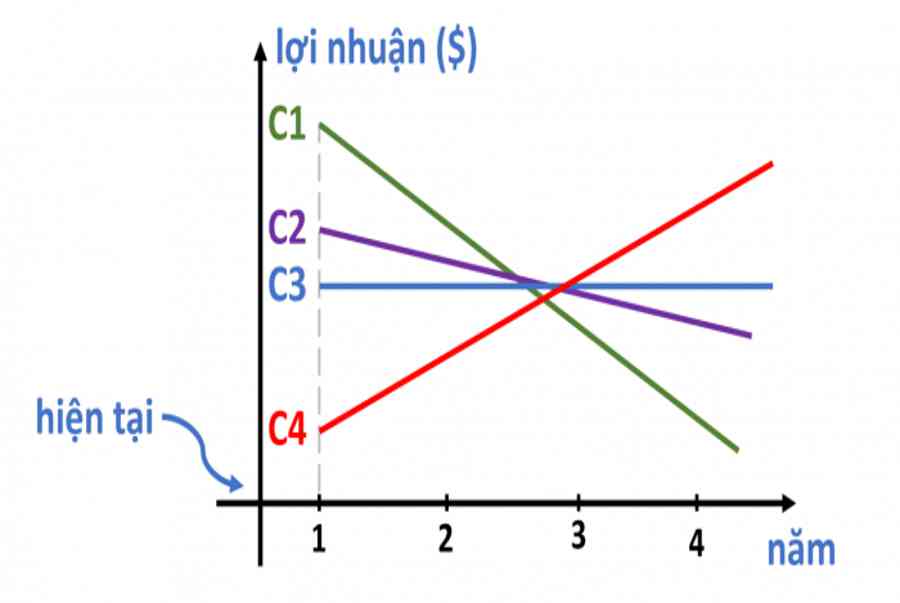
Đồ thị đường thẳng cho ta biết sự tương quan giữa doanh thu thu được và thời hạn tính theo năm .
Chiến lược 1 ( C1 ), đường thẳng có thông số góc USD a_1 = – 2 $ Chiến lược 2 ( C2 ), đường thẳng có thông số góc USD a_2 = – frac { 1 } { 2 } $ Chiến lược 3 ( C3 ), đường thẳng có thông số góc USD a_3 = 0 USD Chiến lược 4 ( C4 ), đường thẳng có thông số góc USD a_4 = 1 USD
Nếu là một vị CEO của công ty và phải quyết định hành động chọn kế hoạch nào để tăng trưởng thì theo bạn, bạn sẽ chọn kế hoạch nào ?
Chiến lược 1 cho ta doanh thu trong thời hạn gần ở mức cao nhất. Các kế hoạch tiếp theo nếu xét trong thời hạn ngắn thì sẽ không mang lại doanh thu cao. Chiến lược thứ 4 là tệ nhất nếu vận dụng ở quy trình tiến độ đầu .
Tuy nhiên, khi nhìn vào thông số góc .
C1 và C2 có $ a = – 2 $ và $ a = – frac { 1 } { 2 } $ là những số âm nên ta biết chắc như đinh doanh thu sẽ giảm dần theo từng năm. C1 có USD vert avert USD lớn hơn nên ta biết rằng nó sẽ giảm nhanh hơn là C2. C3 thì có USD a = 0 $ nên ta chắc như đinh là doanh thu sẽ không tăng cũng như không giảm. Riêng C4 có USD a = 1 > 0 USD nên chắc như đinh doanh thu sẽ tăng theo thời hạn .
Xem thêm : Giờ Pst Là Gì – Giờ Chuẩn Thái Bình Dương
Do đó, về mặt vĩnh viễn, kế hoạch C4 là có lợi nhất khi doanh thu không ngừng tăng mặc dầu xuất phát điểm mà nó mang lại là không cao .
Tốc độ hội tụ

1 Từ quy mô đời sống, ví dụ như sự tăng trưởng của những vi trùng dưới nhiều ảnh hưởng tác động thực tiễn ( thức ăn, môi trường tự nhiên sống, những chất diệt khuẩn, … ), những nhà toán học chuyển dời những mối quan hệ đó sang một phương trình toán học miêu tả nó. Ví dụ gọi sự tăng trưởng của vi trùng là USD x USD, thức ăn là USD a $, chất diệt khuẩn là USD r USD, … rồi họ tìm mối liên hệ giữa USD x, a, r, … $ để màn biểu diễn thành một phương trình theo USD x USD .
Từ đây, thay vì họ triển khai thí nghiệm trong thực tiễn ( với nhiều ngân sách và khó khăn vất vả ) thì họ chỉ việc kiểm soát và điều chỉnh giá trị của những biến và thông số tương ứng. Ví dụ như thay vì giảm lượng thức ăn và tăng liều diệt khuẩn thì họ chỉ việc giảm giá trị của USD a $ và tăng giá trị của USD r USD, …
3 Thường thì các nhà toán học chỉ có thể chứng minh rằng nghiệm chính xác tồn tại nhưng không thể tìm ra được cụ thể nó là gì. Do đó họ nghĩ tới việc tìm một nghiệm xấp xỉ nó, gọi là nghiệm số. Tất nhiên họ sẽ tìm cách làm sao cho nghiệm số này sẽ càng gần nghiệm chính xác càng tốt.
4 Để biết sự sai lệch giữa nghiệm chính xác và nghiệm số này, họ xét tới sai số (error) của chúng, ký hiệu là $e$. Sai số này có mối tương quan với một hằng số $h$ (tôi không giải thích chi tiết nó là gì)được biểu thị qua một đường thẳng có phương trình là
USD USD e = f ( h ) = ah + b $ $
5 Mối tương quan trên cho ta biết rằng khi $h$ càng nhỏ thì nghiệm số sẽ càng “tiến lại gần” nghiệm chính xác. Có rất nhiều phương pháp để tìm nghiệm số khác nhau. Mỗi phương pháp có một cái lợi riêng của nó nhưng điều người ta quan tâm hàng đầu là “tốc độ tiến lại gần” của nghiệm số so với nghiệm chính xác kia. Và hệ số góc $a$ sẽ cho ta biết tốc độ này.
Ta sẽ tìm tổng thể những thông số góc USD a $ của toàn bộ những giải pháp khả dĩ và so sánh chúng. Hệ số góc $ a $ nào có USD vert a vert USD càng lớn tức giải pháp tương ứng đó sẽ càng hiệu suất cao vì khi đó USD e $ sẽ giảm càng nhanh .
Kết
Vậy là bạn đã biết được đôi chút ứng dụng thực tiễn của thông số góc đường thẳng và hiểu rõ hơn khái niệm của nó. Trong bài viết tôi có nhắc tới nhiều định nghĩa và chiêu thức khá lạ. Tôi sẽ có những bài viết tiếp theo nói về chúng, mời bạn đón đọc .
Chuyên mục : Tin Tức
Source: http://139.180.218.5
Category: tản mạn