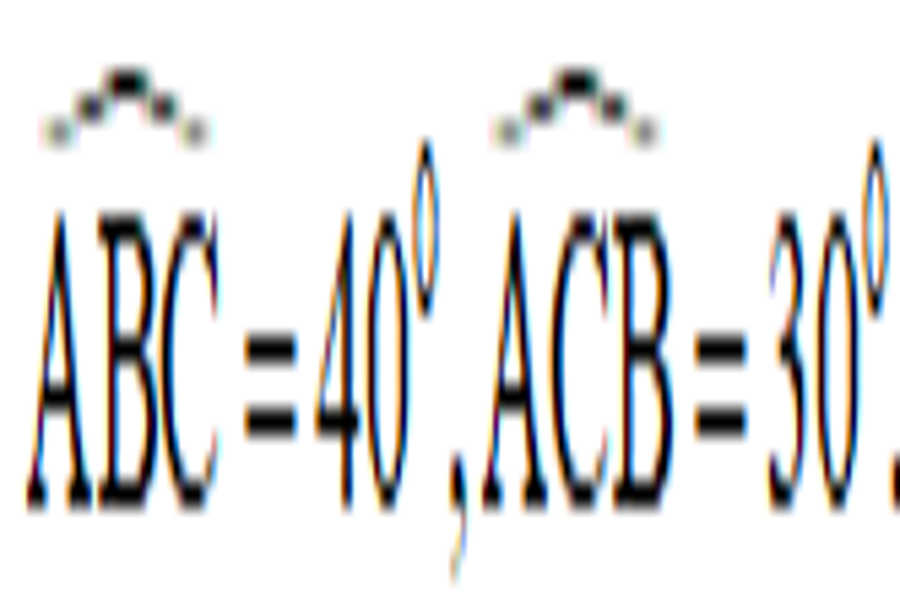Định nghĩa cạnh huyền trong tam giác vuông

Trong một tam giác vuông, cạnh đối lập với góc vuông được gọi là cạnh huyền. Đây cũng chính là cạnh có độ dài lớn nhất trong 3 cạnh của 1 tam giác vuông .

Công thức tính cạnh huyền tam giác vuông

Tính cạnh huyền trong tam giác vuông theo định lý Pytago

Trong định lý Pytago với một tam giác vuông bất kỳ có bình phương chiều dài cạnh huyền bằng tổng bình phương chiều dài hai cạnh góc vuông còn lại

c2 = a2 + b2

Trong đó :

• c là cạnh huyền tam giác vuông
• a, b lần lượt là 2 cạnh góc vuông còn lại

Từ định lý Pythagore, ta hoàn toàn có thể ra được công thức tính cạnh huyền tam giác vuông

Sử dụng định lý sin tìm cạnh huyền trong tam giác vuông

Sin được dùng để chỉ tỉ số giữa những góc hoặc những cạnh trong tam giác vuông. Trong một tam giác vuông, sin của một góc được xác lập bằng chiều dài của cạnh đối lập chia cho cạnh huyền. Với mọi tam giác có cạnh a, b, c và những góc A, B, C thì theo định lý Sin ta có

a/sinA = b/sinB = c/sinC

Lưu ý: Định lý Sin có thể dùng để giải mọi tam giác nhưng để tính cạnh huyền thì chỉ có tam giác vuông mới có.

Tính cạnh huyền trong tam giác vuông đặc biệt

Tam giác vuông đặc biệt quan trọng có chiều dài những cạnh là bộ ba số Pythagore. Bộ ba số Pythagore tiên phong là 3-4-5. Khi thấy một tam giác vuông có 2 cạnh góc vuông là 3 và 4, bạn hoàn toàn có thể xác lập được ngay cạnh huyền của tam giác vuông đó là 5 .
Tam giác vuông đặc biệt quan trọng có số đo 3 góc là 45-45-90 độ. Tam giác này gọi là tam giác vuông cân .
Cạnh của tam giác này có tỉ lệ 1 : 1 : 1 * căn2, nghĩa là 2 cạnh góc vuông bằng nhau và chiều dài cạnh huyền bằng chiều dài cạnh góc vuông nhân với căn bậc hai của 2 .
Tam giác vuông đặc biệt quan trọng có số đo 3 góc là 30-60-90. Các cạnh của tam giác này có tỉ lệ là x : xcăn 3 : 2 x. Nếu cho biết chiều dài 1 cạnh góc vuông thì hoàn toàn có thể tìm ra được chiều dài huyền .

Các dạng bài tập tính cạnh huyền trong tam giác vuông

Ví dụ 1 : Một tam giác vuông có chiều dài bằng 10 cm, cạnh bên bằng 6 cm. Hỏi cạnh còn lại bằng bao nhiêu ?
Lời giải :
Áp dụng công thức tính cạnh huyền trong tam giác vuông ở trên ta có :
a = 8 cm, c = 10 cm
=> c2 = a2 + b2
102 = 82 + b2
100 = 64 + b2
b2 = 100 – 64
b2 = 36
b = 6 cm

Ví dụ 2: Cho tam giác ABC, trong đó BC = 11cm, . Gọi N là chân đường vuông góc hạ từ A xuống cạnh BC. Hãy tính

a ) Độ dài đoạn thẳng AN .
b ) Độ dài cạnh AC .

Lời giải

a) Xét tam giác vuông ANB có: AN = BN.tan40o

Xét tam giác vuông ANC có : AN = CN.tan 30 o
⇒ AN = BN.tan 40 o = CN.tan 30 o
Mà BN = BC – CN = 11 – CN
⇒ ( 11 – CN ). tan40o = CN.tan 30 o
⇔ ( 11 – CN ). 0,84 = CN. 0,58
⇔ 9,24 – 0,84. CN = 0,58 CN
⇔ 1,42. CN = 9,24
⇔ CN ≈ 6,51 ( cm )
⇒ AN = CN.tan 30 o ≈ 6,51. 0,58 ≈ 3,78 ( cm )
b ) Xét tam giác vuông ANC có :

Ví dụ 3 : Cho tam giác ABC vuông tại A đường cao AH. Biết HB = 25 cm, HC = 64 cm. Tính Â, ^ C

Lời giải :
+ ) Xét ΔABC vuông tại A có đường cao AH nên :
AH2 = BH.CH ( hệ thức lượng trong tam giác vuông )
⇔ AH2 = 25.64 = 1600

Ví dụ 4 : Cho tam giác ABC có AB = AC = 50 cm, BC = 60 cm. Các đường cao AD và CE cắt nhau tại H .
a ) Tính độ dài CE .
b ) Tính độ dài CH .
Lời giải :

a ) Tam giác ABC có AB = AC = 50 cm ⇒ ΔABC cân tại A có AD là đường cao nên AD đồng thời là đường trung tuyến và phân giác tại đỉnh A

Ví dụ 5 : Tính cạnh huyền và diện tích quy hoạnh của một tam giác vuông cân nếu a là cạnh góc vuông .

+) Xét tam giác ABC vuông cân tại A có AB = AC = a.

Áp dụng định lý Py – ta – go ta có :

Hy vọng với những kỹ năng và kiến thức về định nghĩa và công thức tính cạnh huyền trong tam giác vuông mà chúng tôi đã trình diễn cụ thể phía trên hoàn toàn có thể giúp những bạn vận dụng giải những bài tập nhanh gọn nhé

Source: http://139.180.218.5
Category: tản mạn