Nội dung chính
I. Đồng quy là gì trong các dạng toán phổ thông?
Đây là một dạng toán thường gặp trong những bài toán hình học và đại số. Vậy ba đường thẳng đồng quy trong toán học là gì ? Cách giải của từng loại toán trong hình học và đại số như thế nào ? Trong môn toán hình học chương trình đại trà phổ thông, đơn cử là môn hình học .
Đó là đường cao trong một tam giác đồng quy là gặp nhau tại trực tâm của tam giác. Tính chất của đồng quy ba đường chéo trong tam giác. “Nếu hai đường cao trong tam giác cắt nhau tại một điểm thì từ đó suy ra đường cao thứ 3 cũng đi qua giao điểm đó”.
Trong môn toán hàm số đại số thì đồng quy là cách chứng tỏ ba đường thẳng bất kỳ đồng quy tại 1 điểm. Đầu tiên ta nên tìm giao điểm của hai trong số ba đường thẳng đó. Sau đó ta chứng tỏ đường thẳng còn lại cũng đi qua giao điểm nói trên .
II. Cách chứng tỏ 3 đường thẳng đồng quy lớp 9
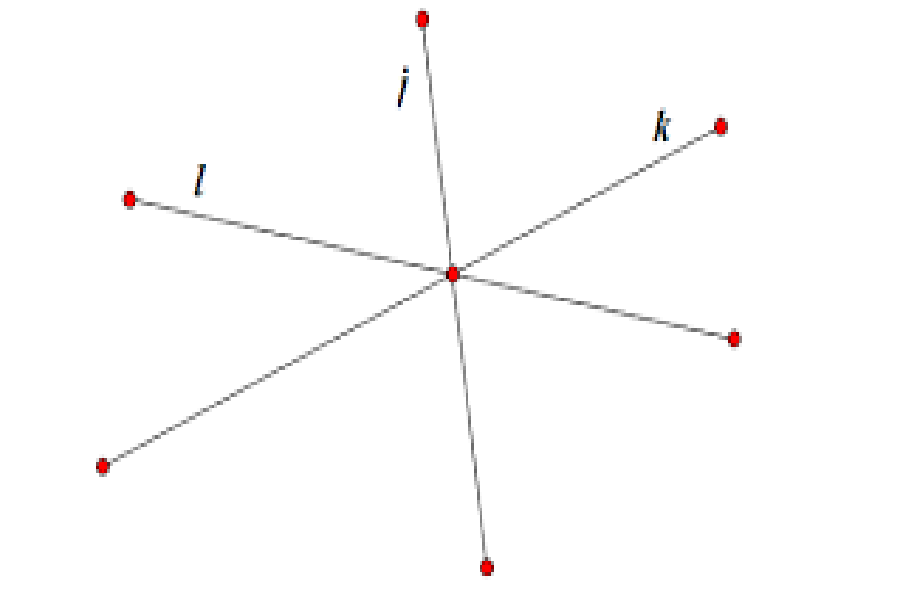
Định nghĩa ba đường thẳng đồng quy : Cho ba đường thẳng lần lượt là i, k, l và không trùng nhau. Ba đường thẳng i, k, l gọi là đồng quy khi ba đường thẳng đó cùng đi qua một điểm chung nào đó .
Có thể vận dụng giải pháp ba đường thẳng đồng quy khi giải những bài toán trong hình học mặt phẳng, hình học khoảng trống và hàm số đại số. Nguyên lý chung là để chứng tỏ ba đường thẳng bất kỳ đồng quy tại 1 điểm. Trước tiên ta tìm giao điểm của hai trong số ba đường thẳng đó. Sau đó chứng tỏ đường thẳng còn lại cũng đi qua giao điểm nói trên .
- Tìm điểm giao nhau của hai đường thẳng. Sau đó chứng tỏ đường thẳng thứ ba cũng đi qua giao điểm đó .
- Sử dụng đặc thù đồng quy trong tam giác .
- Sử dụng chứng tỏ phản chứng : Giả sử ba đường thẳng đã cho không đồng quy. Từ đó dẫn dắt để dẫn đến một điều vô lý. Để chứng tỏ ba đường thẳng đồng quy .
III. Ba đường thẳng đồng quy là gì trong không gian?
Trong khoảng trống cho ba đường thẳng ( I, K, L ). Để chứng tỏ ba đường thẳng này cắt nhau ta hoàn toàn có thể sử dụng hai cách sau đây :
- Cách 1 :
Tìm ( I = A cap B )
Tìm hai mặt phẳng ( ( P. ), ( Q ) ) chứa ( I ) thỏa mãn nhu cầu ( c = ( P. ) cap ( Q ) ). Khi đó hiển nhiên ( I in c ) .
- Cách 2 :
Ta vận dụng định lý : Nếu ( 3 ) mặt phẳng đôi một cắt nhau theo ( 3 ) giao tuyến thì ( 3 ) giao tuyến đó song song hoặc đồng quy .
Áp dụng vào bài toán, ta chỉ cần chứng tỏ ba đường thẳng ( i, k, l ) không đồng phẳng và cắt nhau đôi một .
Ví dụ : Tìm m để 3 đường thẳng đồng quy .
Tìm m để (d1): y = 2x + 1; (d2): y= -x-2 ; (d3): y=(m-1)x – 4
Xem thêm: Đầu số 028 là mạng gì, ở đâu? Cách nhận biết nhà mạng điện thoại bàn – http://139.180.218.5
Hãy tìm m để 3 đường thẳng đồng quy và vẽ hình để minh họa .
Cách giải :
Xét phương trình hoành độ giao điểm của ( d1 ) và ( d2 )
y = 2 x + 1 = – x-2
⇔ 3 x = – 3 ⇔ x = – 1
Suy ra ta có y = 2 ( – 1 ) + 1 = – 1
Như vậy giao điểm của ( d1 ) và ( d2 ) là I ( – 1 ; – 1 )
Để ba đường thẳng trên đồng quy ( cùng giao nhau tại một điểm ) thì điểm I phải thuộc đường thẳng ( d3 )
=> – 1 = ( m – 1 ) ( – 1 ) – 4
⇔ m = – 2
Khi đó thì phương trình đường thẳng ( d3 ) : y = – 3 x – 4

IV. Tính chất ba đường thẳng đồng quy là gì trong hình học?
Khi gặp bài toán chứng tỏ đồng quy thường thì ta đưa ba đường thẳng đó về 3 đường cao trong 1 tam giác hoặc 3 trung tuyến …
- Ba đường trung tuyến trong một tam giác đồng quy tại 1 điểm. Điểm này gọi là trọng tâm của tam giác. Nếu hai đường trung tuyến trong tam giác cắt nhau tại một điểm. Ta suy ra đường trung tuyến thứ 3 cũng đi qua giao điểm đó. Trọng tâm chia đoạn thẳng trung tuyến thành 3 phần chiếm 2/3 độ dài trung tuyến đó .
-
Ba đường phân giác trong một tam giác đồng quy tại 1 điểm. Điểm này gọi là tâm đường tròn nội tiếp tam giác. Nếu hai đường phân giác trong tam giác cắt nhau tại một điểm. Ta suy ra đường phân giác thứ 3 cũng đi qua giao điểm đó. Giao điểm 3 đường phân giác cách đều 3 cạnh của tam giác.
- Ba đường trung trực trong một tam giác đồng quy tại 1 điểm. Điểm này gọi là tâm đường tròn ngoại tiếp tam giác. Nếu hai đường trung trực trong tam giác cắt nhau tại một điểm. Ta suy ra đường trung trực thứ 3 cũng đi qua giao điểm đó. Giao điểm 3 đường trung trực cách đều 3 đỉnh của tam giác .
Đồng quy là gì?Đó là một trong những cách chứng tỏ trong những dạng toán hình học khoảng trống, hình học mặt phẳng và hàm số đại số. Đây là kim chỉ nan cũng như chiêu thức chứng tỏ 3 đường thẳng đồng quy. Một mẹo nhỏ trong khi đi tìm lời giải đáp cho những bài toán trong chương trình đại trà phổ thông .
>>>>> Xem thêm: >> >> > Xem thêm : Muối Axit Là Gì ? 5 Tính Chất Hóa Học Của Muối Của Axit Bạn Nên Biết
Source: http://139.180.218.5
Category: Thuật ngữ đời thường