84 / 100
This entry is part 23 of 69 in the series Học C Không Khó
Tìm bội chung nhỏ nhất của 2 số – Chương trình tìm BCNN của 2 số là một bài tập cơ bản giúp các bạn sinh viên rèn luyện tư duy lập trình. Trong bài viết này, Nguyễn Văn Hiếu sẽ cùng các bạn đi tìm các phương pháp khác nhau để giải bài tập tìm bội chung nhỏ nhất của 2 số nguyên dương. Mỗi cách làm đều sẽ có ý tưởng rõ ràng, cách triển khai và code tìm bcnn minh họa theo cách đó.

Nội dung chính [ẩn đi]
1. Bội chung nhỏ nhất là gì?
Theo Wikipedia ,
Trong số học, bội số chung nhỏ nhất ( hay còn gọi tắt là bội chung nhỏ nhất, viết tắt là BCNN, tiếng Anh : least common multiple hoặc lowest common multiple ( LCM ) hoặc smallest common multiple ) của hai số nguyên a và b là số nguyên dương nhỏ nhất chia hết cho cả a và b. [ 1 ] Tức là nó hoàn toàn có thể chia cho a và b mà không để lại số dư. Nếu a hoặc b là 0, thì không sống sót số nguyên dương chia hết cho a và b, khi đó quy ước rằng LCM ( a, b ) là 0 .
Định nghĩa trên đôi lúc được tổng quát hoá cho hơn hai số nguyên dương : Bội chung nhỏ nhất của a1, …, an là số nguyên dương nhỏ nhất là bội số của a1, …, an .
2. Các thuật toán tìm bội chung nhỏ nhất của 2 số
Ta có một số nhận xét như sau: Theo định nghĩa, BCNN của 2 số a và là số nhỏ nhất chia hết cho cả 2 số a và b. Như vậy, Nếu gọi lcm = BCNN(a, b); Khi đó, ta có thể biết chắc chắn rằng max(a, b) <= lcm <= a*b.
Nắm rõ đặc thù này, ta hoàn toàn có thể đi vào 1 số ít thuật toán tìm BCNN như sau :
C1. Lặp tăng dần cho tới khi tìm được BCNN
Cách này ý tưởng khá là đơn giản, ta chỉ cần tiến hành lặp từ nhỏ tới lớn các số trong đoạn từ [max(a, b),a*b](bao gồm cả 2 đầu mút). Số đầu tiên chia hết cho cả a và b sẽ là BCNN của a và b.
Đánh giá : Cách này trong trường hợp xấu nhất sẽ cần a * b – max ( a, b ) lần lặp. Vẫn với sáng tạo độc đáo này nhưng sẽ được tối ưu ở C2
| 01234567891011121314 |
#include
#include intmain(){ inta=5,b=7,lcm; intmaxV=a *b; for(inti=std::max(a,b);i<=maxV;i++){ if(i%a==0và và i % b = = 0 ) { lcm = i ; break; } } printf(" BCNN ( % d, % d ) = % d ",a,b,lcm); } |
Chạy thử xem sao :
| 012 | BCNN ( 5, 7 ) = 35 |
C2. Tối ưu lặp của cách 1
BCNN của 2 số a và b phải chia hết cho cả 2 số này. Do đó, ta hoàn toàn có thể chỉ cần duyệt qua những số chia hết cho một số ít ( hoặc a, hoặc b ). Nhưng để tối ưu, bạn hãy duyệt qua những số chia hết cho max ( a, b ) .
Ví dụ : a = 5, b = 7. Vậy những số tất cả chúng ta nên duyệt qua những số chia hết cho 7 là 7, 14, 21, 28, 35. Như vậy, tất cả chúng ta giảm được rất nhiều số lần lặp rồi .
Đánh giá: Cách này số lần lặp trong trường hợp xấu nhất là a*b / max(a, b).
| 0123456789101112131415 |
#include
#include intmain(){ inta=5,b=7,lcm; intmaxV=a *b; intstep=std::max(a,b); for(inti=step;i<=maxV;i+=step){ if(i%a==0và và i % b = = 0 ) { lcm = i ; break; } } printf(" BCNN ( % d, % d ) = % d ",a,b,lcm); } |
Chạy thử chương trình :
| 012 | BCNN ( 5, 7 ) = 35 |
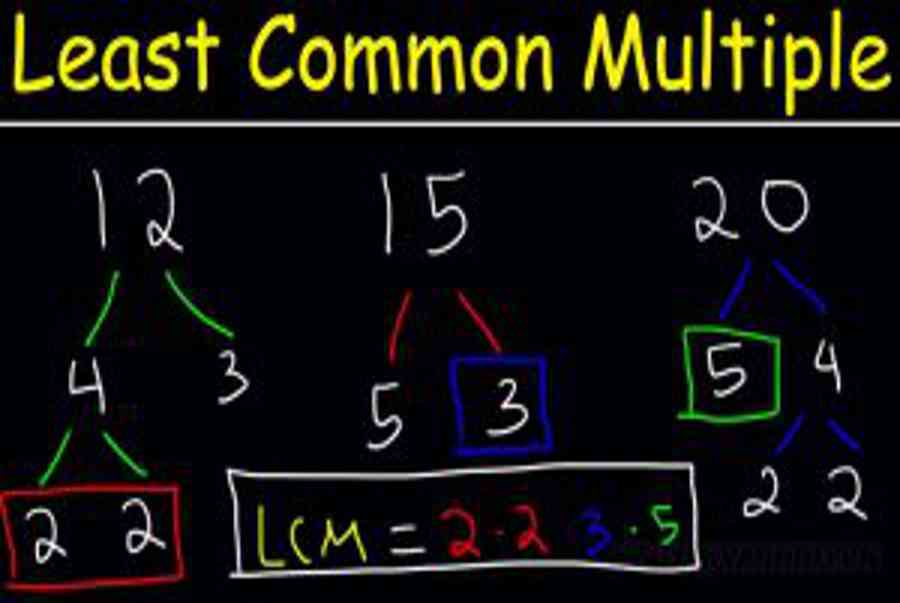
C3. Phân tích thừa số nguyên tố
Sử dụng cách tìm bcnn đã học trong toán cấp 2 :
- Bước 1: Phân tích mỗi số ra thừa số nguyên tố.
- Bước 2: Chọn ra các thừa số nguyên tố chung và riêng.
- Bước 3: Lập tích các thừa số đã chọn, mỗi thừa số lấy với số mũ lớn nhất của nó. Tích đó là BCNN cần tìm.
Cách này mình nhìn nhận chỉ thuận tiện cho thống kê giám sát trên giấy, việc triển khai code phức tạp hơn và vận tốc cũng không quá tốt .
Lưu ý : Để code ngắn gọn nhất, mình sẽ sử dụng những cấu trúc STL của C + + và tính năng for auto của C + + 11
| 012345678910111213141516171819202122232425262728293031323334353637383940414243 |
#include
#include
#include
#include usingnamespacestd; intmain(){ inta=5,b=7,lcm; map set
for(inti=2;a while(a%i==0){ ma[i]++; a/=i; s.insert(i); } } if(a>1){ ma[a]++; s.insert(a); }
for(inti=2;b while(b%i==0){ mb[i]++; b/=i; s.insert(i); } } if(b>1){ mb[b]++; s.insert(b); }
lcm=1; for(autoit:s){ lcm *=pow(it,max(ma[it],mb[it])); } printf(" BCNN ( % d, % d ) = % d ",a,b,lcm); } |
Cách này những bạn hoàn toàn có thể tìm hiểu thêm và bạn hoàn toàn có thể tối ưu thêm. Mình sẽ không lý giải sâu vì trong thực tiễn, thuật toán tìm bcnn này tiến hành khá rườm rà và không tối ưu .
C4. Tìm BCNN của 2 số dựa vào UCLN
Dưới đây là sơ đồ khối tìm bội chung nhỏ nhất của 2 số :
Khi đó, ta có công thức: BCNN(a, b) = a*b / UCLN(a,b)
Các bạn hoàn toàn có thể xem những thuật toán tìm UCLN của 2 số, dưới đây là code tìm hiểu thêm tìm bội chung nhỏ nhất theo UCLN giống sơ đồ khối phía trên :
| 01234567891011121314151617181920212223242526272829 |
#include
#include
#include
#include usingnamespacestd; intgcd(inta,intb){ / / N ? u a = 0 => ucln ( a, b ) = b / / N ? u b = 0 => ucln ( a, b ) = a if(a==0||b==0){ returna+b; } while(a!=b){ if(a>b){ a-=b;/ / a = a - b }else{ b-=a; } } returna;/ / return a or b, b ? i vì lúc này a và b b ? ng nhau } intmain(){ inta=5,b=7; intlcm=a *b/gcd(a,b);
printf(" BCNN ( % d, % d ) = % d ",a,b,lcm); } |
C5. Sử dụng hàm lcm có sẵn ở C++17
Hàm này chỉ có ở C + + 17, và cách sử dụng rất đơn thuần :
| 01234567891011121314 |
#include
#include
#include usingnamespacestd; intmain(){ inta=5,b=7; intans=lcm(a,b);
printf(" BCNN ( % d, % d ) = % d ",a,b,ans); } |
Source: http://139.180.218.5
Category: tản mạn