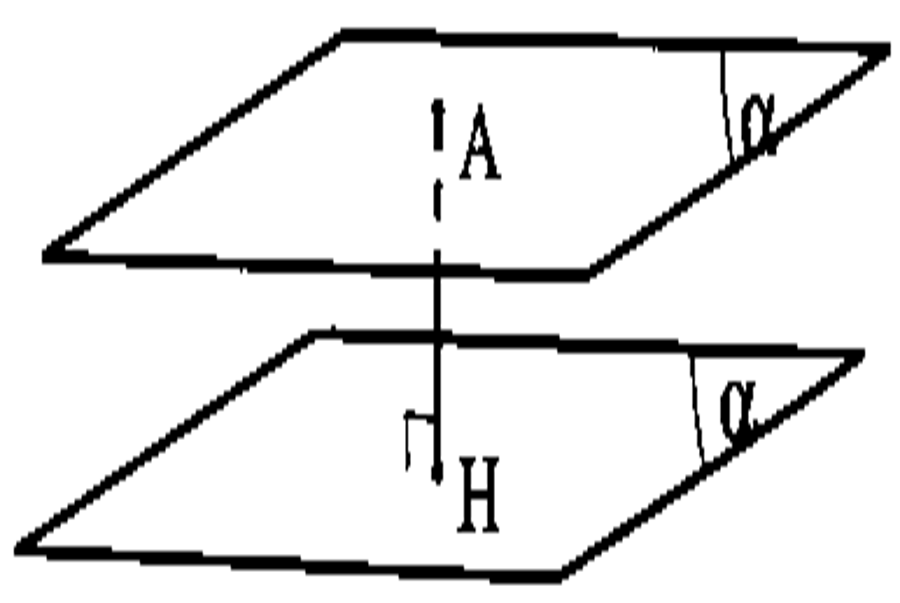
Để tính khoảng cách giữa hai mặt phẳng song song $(\alpha ):ax + by + cz + d = 0$ và $(\beta ):ax + by + cz + D = 0$ $(d \ne D).$ ta dùng công thức tính dưới đây.

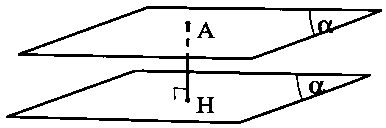
Công thức: $d((\alpha );(\beta ))$ $ = d(A;(\beta ))$ $ = \frac{{|d – D|}}{{\sqrt {{a^2} + {b^2} + {c^2}} }}$ với $A \in (\alpha ).$

Bài tập áp dụng:

Câu 1: Trong không gian với hệ tọa độ $Oxyz$, cho hai mặt phẳng song song $(P):x + y + 3z + 1 = 0$ và $(Q):x + y + 3z + 5 = 0.$ Tính khoảng cách $d$ giữa hai mặt phẳng $(P)$ và $(Q).$

A. $d = \frac{{2\sqrt {11} }}{{11}}.$

B. USD d = \ frac { { 4 \ sqrt { 11 } } } { { 11 } }. $C. USD d = 2 \ sqrt { 11 }. $D. USD d = 11. $

Lời giải:
Chọn $M( – 1;0;0) \in (P)$ $ \Rightarrow d = d((P);(Q))$ $ = \frac{{| – 1 + 5|}}{{\sqrt {{1^2} + {1^2} + {3^2}} }}$ $ = \frac{{4\sqrt {11} }}{{11}}.$
Chọn đáp án B.
Nhận xét: Có thể sử dụng kết quả ở mục A – dạng 2 để chọn nhanh đáp án.

Câu 2: Trong không gian với hệ tọa độ $Oxyz$, gọi $(S)$ là mặt cầu bất kì tiếp xúc với hai mặt phẳng $(P):x + 2y + 2z + 1 = 0$ và $(Q):x + 2y + 2z + 7 = 0.$ Tính bán kính $R$ của mặt cầu $(S).$

A. USD R = 6. $B. USD R = 2. $C. USD R = 1. $D. USD R = 3. $Lời giải :Do USD ( P ) / / ( Q. ) $ $ \ Rightarrow R = \ frac { 1 } { 2 } d ( ( P ) ; ( Q. ) ) $ $ = \ frac { 1 } { 2 }. \ frac { { | 1 – 7 | } } { { \ sqrt { { 1 ^ 2 } + { 2 ^ 2 } + { 2 ^ 2 } } } } = 1. $Chọn đáp án C .Nhận xét : Mọi mặt cầu USD ( S ) USD tiếp xúc đồng thời với mặt phẳng song song USD ( P ) USD, USD ( Q. ) USD đều có nửa đường kính $ R $ bằng nhau và $ R = \ frac { 1 } { 2 } d ( ( P ) ; ( Q. ) ). $

Câu 3: Trong không gian với hệ tọa độ $Oxyz$, cho hai mặt phẳng song song $(\alpha ):2x + y + 2z + 1 = 0$ và $(\beta ):2x + y + 2z + 3 = 0.$ Tính tổng khoảng cách $d$ từ gốc tọa độ $O$ đến hai mặt phẳng $(\alpha )$ và $(\beta ).$

A. $ d = \ frac { 2 } { 3 }. $B. USD d = \ frac { 4 } { 3 }. $C. USD d = 2. $D. USD d = \ frac { 1 } { 3 }. $Lời giải :Ta có : USD d ( O ; ( \ alpha ) ) = \ frac { { | 1 | } } { { \ sqrt { { 2 ^ 2 } + { 1 ^ 2 } + { 2 ^ 2 } } } } = \ frac { 1 } { 3 } $ và USD d ( O ; ( \ beta ) ) = \ frac { { | 3 | } } { { \ sqrt { { 2 ^ 2 } + { 1 ^ 2 } + { 2 ^ 2 } } } } = 1 USD suy ra :USD d = { d_1 } + { d_2 } = \ frac { 4 } { 3 }. $Chọn đáp án B .

Câu 4: Trong không gian với hệ tọa độ $Oxyz$, tìm tập hợp tất cả các giá trị thực của tham số $m$ sao cho khoảng cách giữa hai mặt phẳng $(P):x + 2y + 2z + 2 = 0$ và $(Q):x + 2y + 2z + 2m – 1 = 0$ bằng $1.$

A. $ \ { 3 \ }. $B. $ \ { 3, – 3 \ }. $C. $ \ { 0,3 \ }. $D. USD \ { 0, – 3 \ }. $Lời giải :Chọn USD M ( – 2 ; 0 ; 0 ) \ in ( P ) $ $ \ Rightarrow d ( ( P ) ; ( Q. ) ) $ $ = d ( M ; ( Q. ) ) $ $ = \ frac { { | 2 m – 3 | } } { 3 }. $Theo giả thiết : $ \ frac { | 2 m-3 | } { 3 } = 1 \ Leftrightarrow | 2 m-3 | = 3 \ Leftrightarrow \ left [ \ begin { array } { l } 2 m-3 = 3 \ \ 2 m-3 = – 3 \ end { array } \ Leftrightarrow \ left [ \ begin { array } { l } m = 3 \ \ m = 0 \ end { array } \ right. \ right. $Chọn đáp án C .

Câu 5: Trong không gian với hệ tọa độ $Oxyz$, cho hai điểm $A(1;1;1)$ và $B(2;1;-1).$ Gọi $\vec n = (1;a;b)$, $(a;b \in R)$ là một vectơ pháp tuyến của mặt phẳng $(P)$ qua $A$ và cách $B$ một khoảng lớn nhất. Tính $a + b.$

A. USD 2. $B. USD 3. $C. USD – 2. $D. USD – 3. $Lời giải :

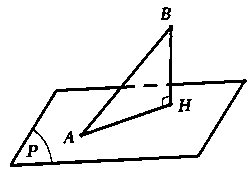
Gọi $ H $ là hình chiếu vuông góc của $ B $ trên mặt phẳng USD ( P ) USD, ta có :USD d ( B ; ( P ) ) = BH \ le AB $ $ \ Rightarrow d { ( B ; ( P ) ) _ { \ max } } = AB. $Vậy USD ( P ) USD là mặt phẳng qua $ A $ và có một vectơ pháp tuyến là $ \ overrightarrow { AB } = ( 1 ; 0 ; – 2 ). $Suy ra USD a = 0 $ và $ b = – 2 $ $ \ Rightarrow a + b = – 2. $

Chọn đáp án C.

Câu 6: Trong không gian với hệ tọa độ $Oxyz$, cho bốn điểm $A(1;1;0)$, $B(3;1; – 2)$, $C(0;2;0)$ và $D( – 1;3;2).$ Có bao nhiêu mặt phẳng chứa $B$, $C$ và cách đều hai điểm $A$, $D$?

A. USD 0. $B. USD 1. $C. USD 2. $D. Vô số .Lời giải :Kiểm tra được : $ [ \ overrightarrow { AB }, \ overrightarrow { AC } ]. \ overrightarrow { AD } = – 4 \ ne 0 $ $ \ Rightarrow A $, USD B USD, USD C USD, USD D $ không đồng phẳng .Vậy sống sót hai mặt phẳng chứa USD B USD, $ C $ và cách đều hai điểm $ A $, USD D $ là :+ Trường hợp 1 : Mặt phẳng chứa USD B USD, $ C $ và song song với đường thẳng $ AD. $

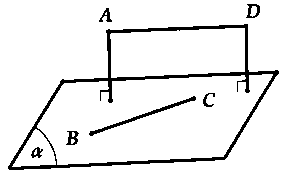
+ Trường hợp 2 : Mặt phẳng chứa USD B USD, $ C $ và đi qua trung điểm USD I $ của đoạn thẳng $ AD. $

Chọn đáp án C .

Câu 7: Trong không gian với hệ tọa độ $Oxyz$, cho bốn điểm $A(1;1;0)$, $B(3;1; – 2)$, $C(0;2;0)$ và $D( – 1;3;2).$ Biết rằng qua $B$, $C$ có hai mặt phẳng cách đều $A$, $D.$ Tính tổng khoảng cách từ $O$ đến hai mặt phẳng đó.

A. $ \ frac { { 9 \ sqrt { 10 } + 5 \ sqrt 6 } } { 5 }. $B. $ \ frac { { 3 \ sqrt { 10 } + 5 \ sqrt 6 } } { { 15 } }. $C. $ \ frac { { 9 \ sqrt { 10 } + 5 \ sqrt 6 } } { { 15 } }. $D. $ \ frac { { 9 \ sqrt { 10 } + 7 \ sqrt 6 } } { { 15 } }. $Lời giải :Kiểm tra được : $ [ \ overrightarrow { AB }, \ overrightarrow { AC } ]. \ overrightarrow { AD } \ ne 0 $ $ \ Rightarrow A $, USD B USD, USD C USD, USD D $ không đồng phẳng. Vậy sống sót hai mặt phẳng chứa USD B USD, $ C $ và cách đều hai điểm $ A $, USD D $ là :+ Trường hợp 1 : Mặt phẳng chứa USD B USD, $ C $ và song song với đường thẳng $ AD. $

Mặt phẳng USD ( P ) USD qua USD C ( 0 ; 2 ; 0 ) USD và có một vectơ pháp tuyến là $ { \ vec n_p } = [ \ overrightarrow { BC }, \ overrightarrow { AD } ] = ( – 2 ; 2 ; – 4 ) USD, có phương trình :USD ( P ) : – 2 ( x – 0 ) + 2 ( y – 2 ) – 4 ( z – 0 ) = 0 $ $ \ Leftrightarrow x – y + 2 z + 2 = 0. $+ Trường hợp 2 : Mặt phẳng chứa USD B USD, $ C $ và đi qua trung điểm USD I $ của đoạn thẳng $ AD. $

Trung điểm USD I $ của $ AD $ là USD I ( 0 ; 2 ; 1 ). $ Mặt phẳng USD ( Q. ) USD qua USD C ( 0 ; 2 ; 0 ) USD và có một vectơ pháp tuyến là $ { \ vec n_Q } = [ \ overrightarrow { BC }, \ overrightarrow { IB } ] = ( – 1 ; – 3 ; 0 ) USD, có phương trình :USD ( Q. ) : – 1 ( x – 0 ) – 3 ( y – 2 ) – 0 ( z – 0 ) = 0 $ $ \ Leftrightarrow – x – 3 y + 6 = 0. $Vậy USD d ( O ; ( P ) ) + d ( O ; ( Q. ) ) $ $ = \ frac { { 9 \ sqrt { 10 } + 5 \ sqrt 6 } } { { 15 } }. $Chọn đáp án B .

Câu 8: Trong không gian với hệ tọa độ $Oxyz$, cho bốn điểm $A(1;1;0)$, $B(3;1; – 2)$, $C(0;2;0)$ và $D( – 1;3;2).$ Gọi $\vec n(1;b;0)$, $(b \in R)$ là một vectơ pháp tuyến của mặt phẳng qua $B$, $C$ và cách đều $A$, $D.$ Tính ${b^2}.$

A. USD 16. $B. USD 1. $C. USD 4. USDD. USD 9. $Lời giải :Kiểm tra được : $ | \ overrightarrow { A B }, \ overrightarrow { A C } ]. \ overrightarrow { A D } = – 4 \ neq 0 \ Rightarrow A, B, C, D $ không đồng phẳng. Vậy sống sót hai mặt phẳng chứa USD B USD, $ C $ và cách đều hai điểm $ A $, USD D $ là :+ Trường hợp 1 : Mặt phẳng chứa USD B USD, $ C $ và song song với đường thẳng $ AD. $Mặt phẳng USD ( P ) USD qua USD C ( 0 ; 2 ; 0 ) USD và có một vectơ pháp tuyến là $ { \ vec n_P } = [ \ overrightarrow { BC }, \ overrightarrow { AD } ] = ( – 2 ; 2 ; – 4 ). $+ Trường hợp 2 : Mặt phẳng chứa USD B USD, $ C $ và đi qua trung điểm USD I $ của đoạn thẳng $ AD. $Trung điểm USD I $ của $ AD $ là USD I ( 0 ; 2 ; 1 ). $Mặt phẳng USD ( Q. ) USD qua USD C ( 0 ; 2 ; 0 ) USD và có một vectơ pháp tuyến là $ { \ vec n_Q } = [ \ overrightarrow { BC }, \ overrightarrow { IB } ] = ( – 1 ; – 3 ; 0 ). $

Theo giả thiết $\vec n(1;b;0)$ $ = {\vec n_Q} = ( – 1; – 3;0)$ $ \Rightarrow b = 3.$

Vậy $ { b ^ 2 } = 9. $Chọn đáp án D .Tin tức – Tags: hình học không gian, khoảng cách, mặt phẳng, song song

Source: http://139.180.218.5
Category: tản mạn