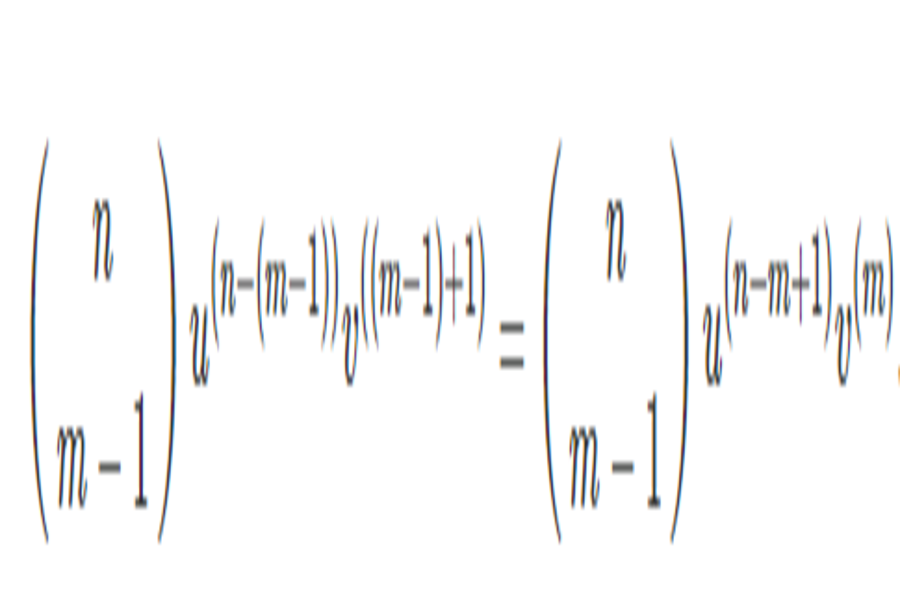Định lý Leibnitzvề cơ bản là quy tắc Leibnitz được xác lập cho đạo hàm của phản đạo hàm .Theo quy tắc, đạo hàm bậc n của tích hai hàm có thể được biểu diễn với sự trợ giúp của công thức. Các hàm có thể có chức năng đã cho dưới dạng một đạo hàm được gọi là các đạo hàm ngược (hoặc nguyên hàm) của hàm. Công thức cung cấp tất cả các đạo hàm này được gọi là tích phân không xác định của hàm, và quá trình tìm kiếm các đạo hàm như vậy được gọi là tích phân. Bây giờ chúng ta hãy thảo luận ở đây về công thức và chứng minh của quy tắc Leibnitz.

Công thức Định lý Leibnitz

Giả sử có hai hàm u ( t ) và v ( t ) có đạo hàm đến bậc n. Bây giờ tất cả chúng ta hãy xem xét đạo hàm của tích của hai hàm này .

Đạo hàm đầu tiên có thể được viết là;

( uv ) ‘ = u’v + uv ’
Bây giờ nếu tất cả chúng ta phân biệt biểu thức trên một lần nữa, tất cả chúng ta nhận được đạo hàm cấp hai ;
( uv ) ”
= [ ( uv ) ‘ ] ’
= ( u’v + uv ‘ ) ’
= ( u’v ) ‘ + ( uv ’ ) ‘
= u ′ ′ v + u ′ v ′ + u ′ v ′ + uv ′ ′
= u ′ ′ v + 2 u ′ v ′ + uv ′ ′
Tương tự, tất cả chúng ta hoàn toàn có thể tìm thấy đạo hàm cấp ba ;
( uv ) ′ ′ ′
= [ ( uv ) ′ ′ ] ′
= ( u ′ ′ v + 2 u ′ v ′ + uv ′ ′ ) ′
= ( u ′ ′ v ) ′ + ( 2 u ′ v ′ ) ′ + ( uv ′ ′ ) ′
= u ′ ′ ′ v + u ′ ′ v ′ + 2 u ′ ′ v ′ + 2 u ′ v ′ ′ + u ′ v ′ ′ + uv ′ ′ ′
= u ′ ′ ′ v + 3 u ′ ′ v ′ + 3 u ′ v ′ ′ + uv ′ ′ ′
Bây giờ nếu tất cả chúng ta so sánh những biểu thức này, nó được thấy rất giống với khai triển nhị thức được nâng lên thành số mũ. Nếu tất cả chúng ta xem xét những số hạng có số mũ 0, u 0 và v 0 tương ứng với chính những hàm u và v, tất cả chúng ta hoàn toàn có thể tạo ra công thức cho tích đạo hàm bậc n của hai hàm, theo cách đó ;

Công thức này được gọi là công thức Quy tắc Leibniz và có thể được chứng minh bằng quy nạp.

Chứng minh định lý Leibnitz

Giả sử rằng những hàm u ( t ) và v ( t ) có đạo hàm bậc ( n + 1 ). Bằng quan hệ tái diễn, tất cả chúng ta hoàn toàn có thể trình diễn đạo hàm của ( n + 1 ) bậc theo cách sau :

Sau khi phân biệt, chúng tôi nhận được ;

Tổng ở phía bên phải hoàn toàn có thể được tích hợp với nhau để tạo thành một tổng duy nhất, vì những số lượng giới hạn cho cả hai tổng là như nhau. Bây giờ, tất cả chúng ta hãy lấy một chỉ số trung gian sao cho 1 ≤ m ≤ n. Vì vậy, khi i = m, thì số hạng tiên phong hoàn toàn có thể được viết là ;

Số hạng thứ hai khi i = m-1 sẽ là ;

Khi thêm hai thuật ngữ này, chúng tôi nhận được ;

Chúng tôi biết từ khái niệm tổng hợp rằng ;

Dựa trên khái niệm trên, tất cả chúng ta hoàn toàn có thể viết tổng của hai số hạng này, khi i = m và khi i = m-1, as ;

Từ biểu thức trên, tất cả chúng ta hoàn toàn có thể thấy khi giá trị của m đổi khác từ 1 đến n, tổng hợp được tạo ra này sẽ gồm có toàn bộ những số hạng từ i = 1 đến i = n, nhưng không có i = 0 trong số hạng tiên phong và i = 1 trong số hạng thứ hai bằng ;

Do đó, đạo hàm tác dụng của ( n + 1 ) bậc của tích hai hàm được cho bởi ;

Xem thêm: 

Source: http://139.180.218.5
Category: tản mạn