Rate this post

Trong toán học nói chung và môn hình học nói riêng thì chúng ta thường xuyên gặp phải hình chóp tứ giác đều trong mỗi bài toán .Nhưng cũng không phải là ai cũng biết cách xác định hay tính được các thể tích và diện tích của hình chóp tứ giác đều. Chính vì thế hôm nay Legoland xin tổng hợp lại cho mọi người các kiến thức về hình chóp tứ giác nhé .

Hình chóp tứ giác đều là gì?

Hình chóp tứ giác đều là hình chóp có đáy là hình vuông vắn và đường cao của chóp đi qua tâm đáy ( giao của 2 đường chéo hình vuông vắn ) .

Tính chất :

• Là hình chóp tứ giác có đáy là hình vuông
• Tất cả các cạnh bên của hình chóp tứ giác có kích thước bằng nhau
• Tất cả các góc tạo bởi các mặt bên và mặt đáy đều bằng nhau
• Tất cả các mặt bên của hình chóp từ giác là các tam giác cân bằng nhau
• Điểm kéo từ đỉnh chóp xuống tâm của mặt đáy chính là chiều cao của hình chóp tứ giác đều
• Tất cả các góc tạo bởi cạnh bên và mặt đáy bằng nhau

Công thức tính diện tích hình chóp tứ giác đều

Tính diện tích xung quanh hình chóp tứ giác :

Để tính được diện tích xung quanh của hình chóp tứ giác thì tất cả chúng ta sẽ được tính bằng tích của nửa chu vi đáy với trung đoạn. Cụ thể công thức ký hiệu như sau :

Sxq = p.d

Trong đó :

• p là nửa chu vi đáy
• d là trung đoạn

Tham khảo thêm :

Công thức tính diện tích toàn phần hình chóp tứ giác: 

Diện tích toàn phần của hình chóp tứ giác sẽ bằng tổng của diện tích xung quanh và diện tích dưới mặt đáy. Ta có công thức sau đây :

Stp = Sxq + S

Trong đó :

• S là diện tích đáy
• Sxp : là diện tích xung quanh chúng ta áp dụng công thức ở trên để tính

Ví dụ : 

Cho hình chóp tứ giác đều có cạnh đáy dài 8 cm, độ dài các cạnh bên là 7cm. Tính diện tích xung quanh và diện tích toàn phần.

Lời giải :

Bài toán cho hình chóp tam giác đều, như vậy đáy hình chóp sẽ là tam giác đều cạnh 6 cm, chiều dài các cạnh bên là 5cm.

Để tính được diện tích xung quanh và diện tích toàn phần của hình chóp ta cần tính thêm độ dài trung đoạn hình chóp .
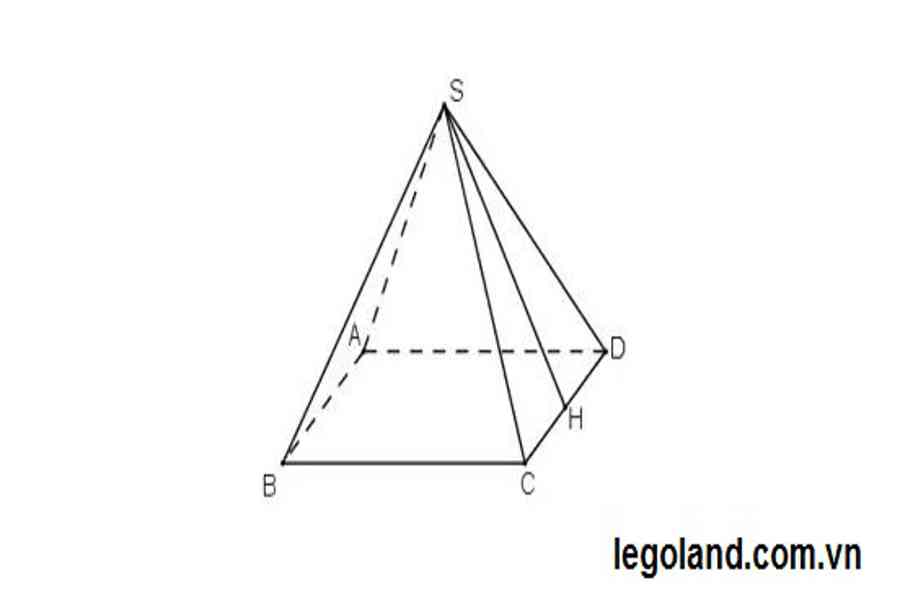
Các bạn vẽ hình chóp tam giác đều SABCD như hình ảnh. Từ đỉnh S, vẽ đường thẳng nối với trung điểm của đoạn AC, ta đặt là điểm M. SM chính là trung đoạn của hình chóp .
Xét tam giác SBM, vì SBC là tam giác cân nên ta có SBM là tam giác vuông, vận dụng định lý Pitago cho tam giác này ta tính được cạnh SM. SM ^ 2 = SB ^ 2 – BM ^ 2 = 8 ^ 2 – 4 ^ 2 => SM = ~ 7 cm .

Diện tích xung quanh hình chóp là: Sxq = p.d = 1⁄2 x 7 x 7 x 7 = 10,5 cm2

Diện tích toàn phần hình chóp là: Stp = Sxq + Sđáy = 10,5 + 64 = 74,5 cm2

Công thức tính thể tích hình chóp tứ giác 

Trong đó :

• SABCD là diện tích hình vuông ABCD
• SO là đường cao kẻ từ O xuống tâm đáy ABCD

Ví dụ :

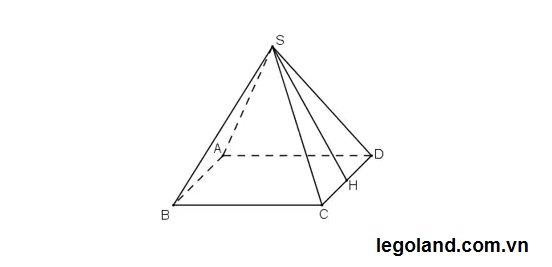
Cho hình chóp tứ giác S.ABCD, đáy ABCD là hình vuông cạnh bằng a, cạnh bên SA vuông góc với mặt phẳng đáy và SC tạo với mặt đáy một góc bằng 60 độ. Tính thể tích khối chóp S.ABCD.. Như hình vẽ sau :

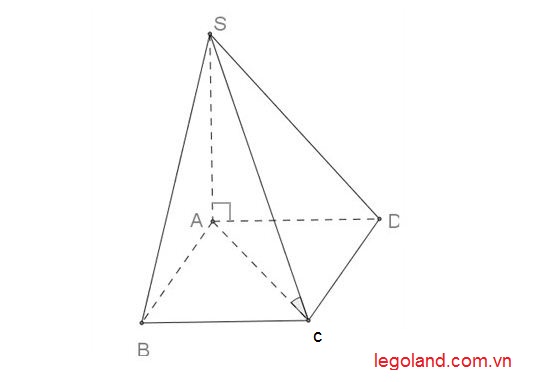
Lời giải :

Theo công thức tính thể tích hình chóp 

thì những bạn cần tính được độ cao và diện tích mặt dưới hình chóp tứ giác .

• Diện tích hình vuông ABCD:

• Tính chiều cao hình chóp:

AC là hình chiếu của SC trên mặt phẳng ( ABCD ) nên ta có :

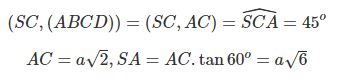
Sau khi tính được diện tích hình vuông ABCD và chiều cao hình chóp cuối cùng các bạn sẽ tính

Vậy thể tích hình chóp tứ giác đều là :

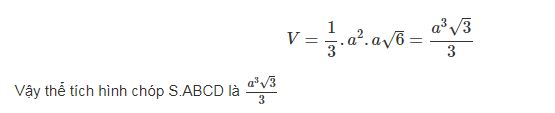
Tổng kết : 

Như thế là tất cả chúng ta đã hiểu hơn về hình chóp tứ giác đều và những công thức tính diện tích và thể tích của hình chóp tứ giác đều rồi chứ. Chúc những bạn thành công xuất sắc .

Source: http://139.180.218.5
Category: tản mạn