Khái niệm về đa giác.

Đa giác ABCDE (hình 114, hình 117) là hình gồm năm đoạn thẳng AB, BC, CD, DE, EA, trong đó bất kì hai đoạn thẳng nào có một điểm chung cũng không cùng nằm trên một đoạn thẳng. Các điểm A, B, C, D, E được gọi là các đỉnh, các đoạn thẳng AB, BC, CD, DE, EA được gọi là các cạnh của đa giác đó.

Định nghĩa đa giác lồi

Đa giác lồi là đa giác luôn nằm trong một nửa mặt phẳng có bờ là đường thẳng chứa bất kì cạnh nào của đa giác đó.

Chú ý: Từ nay nếu nói đa giác mà không nói gì thêm, ta hiểu đó là đa giác lồi.
Quan sát đa giác ở hình 119, ta có thể điền như sau:

Hinh 119.

Các đỉnh là các điểm A, B, C, D, E, G
Các đỉnh kề nhau là A và B, hoặc B và C, hoặc C và D, hoặc D và E, hoặc E và G, hoặc G và A.
Các cạnh là các đoạn thẳng AB, BC, CD, DE, EG, GA.
Các đường chéo là các đoạn nối hai đỉnh không kề nhau AC, CG, AD, AE, BG, BE, BD
Các góc là $\widehat{A}$, $\widehat{B}$, $\widehat{C}$, $\widehat{D}$, $\widehat{E}$, $\widehat{G}$
Các điểm nằm trong đa giác (các điểm trong của đa giác) là M, N, P
Các điểm nằm ngoài đa giác (các điểm ngoài của đa giác) là Q, R
Đa giác có n đỉnh (n $\geq$ 3) gọi là hình n-giác hay hình n cạnh. Với n = 3, 4, 5, 6, 8 ta thường gọi là tam giác, tứ giác, ngũ giác, lục giác, bát giác. Với n = 7, 9, 10, … ta gọi là hình 7 cạnh, hình 9 cạnh, hình 10 cạnh, …

Đa giác đều

Hình 120a, b, c, d là những ví dụ về đa giác đều.

Định nghĩa đa giác đều

Đa giác đều là đa giác có tất cả các cạnh bằng nhau và tất cả các góc bằng nhau.

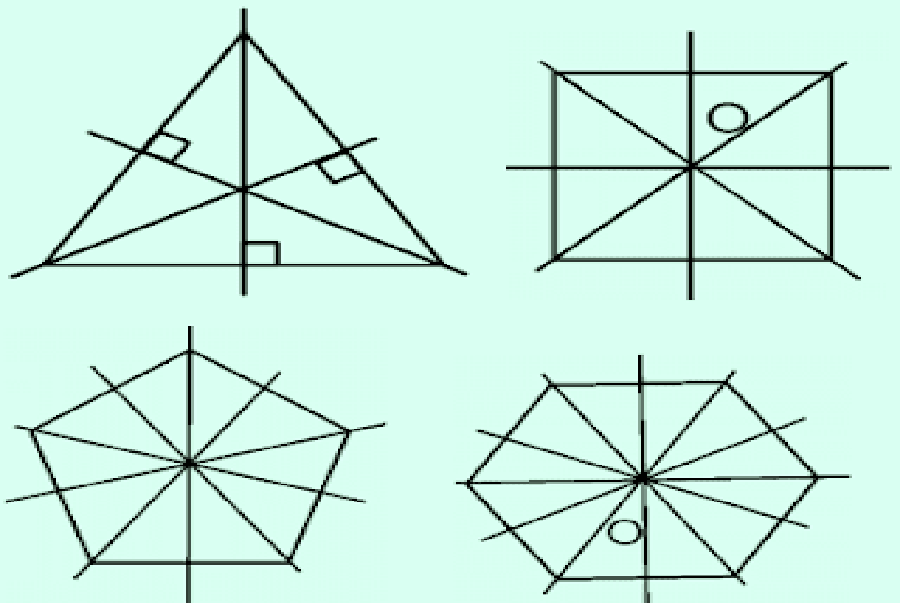
Hình 120.

Sau khi vẽ các trục đối xứng và tâm đối xứng hình 120, ta có nhận xét như sau:
– Tam giác đều có ba trục đối xứng.
– Hình vuông có bốn trục đối xứng và điểm O là tâm đối xứng.
– Ngũ giác đều có năm trục đối xứng.
– Lục giác đều có 6 trục đối xứng và một tâm đối xứng.

Mỗi bài toán có nhiều cách giải, đừng quên chia sẻ cách giải hoặc ý kiến đóng góp của bạn ở khung nhận xét bên dưới. Xin cảm ơn!

CÙNG CHIA SẺ ĐỂ KIẾN THỨC ĐƯỢC LAN TỎA !

Bài học liên quan.

Ta biết tam giác là hình gồm ba đoạn thẳng, tứ giác là hình gồm 4 đoạn thẳng và cứ thêm một đoạn thẳng, ta có một hình mới. Các hình đó có một tên gọi chung là đa giác Đa giác ABCDE ( hình 114, hình 117 ) là hình gồm năm đoạn thẳng AB, BC, CD, DE, EA, trong đó bất kể hai đoạn thẳng nào có một điểm chung cũng không cùng nằm trên một đoạn thẳng. Các điểm A, B, C, D, E được gọi là những đỉnh, những đoạn thẳng AB, BC, CD, DE, EA được gọi là những cạnh của đa giác đó. Các đa giác ở hình 115, 116, 117 được gọi là những đa giác lồi. Từ nay nếu nói đa giác mà không nói gì thêm, ta hiểu đó là đa giác lồi. Quan sát đa giác ở hình 119, ta hoàn toàn có thể điền như sau : Các đỉnh là những điểm A, B, Các đỉnh kề nhau là A và B, hoặc B và C, Các cạnh là những đoạn thẳng AB, BC, Các đường chéo là những đoạn nối hai đỉnh không kề nhau AC, CG, AD, AE, BG, BE, BDCác góc là $ \ widehat { A } $, $ \ widehat { B } $, Các điểm nằm trong đa giác ( những điểm trong của đa giác ) là M, N, PCác điểm nằm ngoài đa giác ( những điểm ngoài của đa giác ) là Q., RĐa giác có n đỉnh ( n $ \ geq USD 3 ) gọi là hình n-giác hay hình n cạnh. Với n = 3, 4, 5, 6, 8 ta thường gọi là tam giác, tứ giác, ngũ giác, lục giác, bát giác. Với n = 7, 9, 10, … ta gọi là hình 7 cạnh, hình 9 cạnh, hình 10 cạnh, … Hình 120 a, b, c, d là những ví dụ về đa giác đều. Sau khi vẽ những trục đối xứng và tâm đối xứng hình 120, ta có nhận xét như sau : – Tam giác đều có ba trục đối xứng. – Hình vuông có bốn trục đối xứng và điểm O là tâm đối xứng. – Ngũ giác đều có năm trục đối xứng. – Lục giác đều có 6 trục đối xứng và một tâm đối xứng .

Source: http://139.180.218.5
Category: tản mạn