- Chuyên đề: Các trường hợp bằng nhau của tam giác vuông
- A. Lý thuyết
- B. Trắc nghiệm & Tự luận
- Video liên quan
Nội dung chính
Chuyên đề: Các trường hợp bằng nhau của tam giác vuông
- A. Lý thuyết
- B. Trắc nghiệm & Tự luận
A. Lý thuyết
1. Các trường hợp bằng nhau đã biết của tam giác vuông
Nếu hai cạnh góc vuông của tam giác vuông này lần lượt bằng hai cạnh góc vuông của tam giác vuông kia thì hai tam giác đó bằng nhau (cạnh góc cạnh).
Bạn đang đọc: Bài tập trường hợp bằng nhau của tam giác vuông
Nếu một cạnh góc vuông và một góc nhọn kề cạnh ấy của tam giác vuông này bằng một cạnh góc vuông và một góc nhọn kề cạnh ấy của tam giác vuông kia thì hai tam giác vuông đó bằng nhau .
Nếu cạnh huyền và một góc nhọn của tam giác vuông này bằng cạnh huyền và một góc nhọn của tam giác vuông kia thì hai tam giác đó bằng nhau .
2. Trường hợp bằng nhau về cạnh huyền, cạnh góc vuông
Nếu cạnh huyền và một cạnh góc vuông của tam giác vuông này bằng cạnh huyền và một cạnh góc vuông của tam giác vuông kia thì hai tam giác vuông đó bằng nhau .
B. Trắc nghiệm & Tự luận
I. Câu hỏi trắc nghiệm
Bài 1: Cho tam giác ABC và tam giác NPM có BC = PM, B = P = 90°. Cần điều kiện gì để tam giác ABC bằng tam giác NPM theo trường hợp cạnh huyền cạnh góc vuông?
A. BA = PM B. BA = PN C. CA = MN D. A = NTa có hai tam giác ABC và tam giác NPM có BC = PM, B = P = 90 ° mà BC, PM là hai cạnh góc vuông của tam giác ABC và NPM nên để hai tam giác bằng nhau theo trường hợp cạnh huyền cạnh góc vuông thì ta cần thêm điều kiện kèm theo CA = MNChọn đáp án C .
Bài 2: Cho tam giác ABC và tam giác MNP có A = M = 90°, C = P. Cần điều kiện gì để hai tam giác ABC và tam giác MNP bằng nhau theo trường hợp cạnh góc vuông góc nhọn kề?
A. AC = MP B. AB = MN C. BC = NP D. AC = MNTa có : C = P mà góc C và góc P. là hai góc nhọn kề của tam giác ABC và tam giác MNPDo đó để tam giác ABC và tam giác MNP bằng nhau theo trường hợp cạnh hóc vuông góc nhọn kề thì cần thêm điều kiện kèm theo AC = MPChọn đáp án A .
Bài 3: Cho tam giác ABC và tam giác DEF có: B = E = 90°, AC = DF, A = F. Phát biểu nào sau đây đúng?
A. ΔABC = ΔFEDB. ΔABC = ΔFDEC. ΔBAC = ΔFEDD. ΔABC = ΔDEFXét tam giác ABC và tam giác FED có :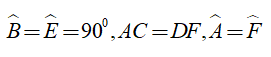 Suy ra ΔABC = ΔFEDChọn đáp án A .
Suy ra ΔABC = ΔFEDChọn đáp án A .
Bài 4: Cho tam giác ABC và tam giác KHI có: A = K = 90°, AB = KH, BC = HI. Phát biểu nào sau đây đúng?
A. ΔABC = ΔKHIB. ΔABC = ΔHKIC. ΔABC = ΔKIHD. ΔACB = ΔKHIXét tam giác ABC và tam giác KHI có :A = K = 90 °, AB = KH, BC = HI
ΔABC = ΔKHIChọn đáp án A
Bài 5: Cho tam giác ABC và tam giác DEF có AB = DE, B = E, A = D = 90°. Biết AC = 9cm. Tính độ dài DF?
A. 10 cm B. 5 cm C. 9 cm D. 7 cmXét tam giác ABC và tam giác DEF có :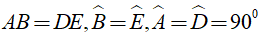
ΔABC = ΔDEF. Khi đó AC = DF = 9 cmChọn đáp án C
II. Bài tập tự luận
Bài 1: Cho tam giác ABC cân tại A, kẻ AD vuông góc với BC. Chứng minh rằng AD là tia phân giác của góc A?Đáp án
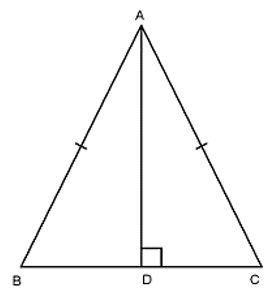
Xét hai tam giác vuông ADB và ADC cóAD chungAB = AC ( gt )Nên ΔADB = ΔADC ( cạnh huyền cạnh góc vuông )Suy ra BAD = CAD ( góc tương ứng bằng nhau )Do đó AD là tia phân giác của góc A .Vậy AD là tia phân giác của góc A .
Bài 2: Cho tam giác ABC cân tại A, kẻ BH AC, CK AB. Gọi I là giao điểm của BH và CK. Chứng minh AI là tia phân giác của góc A.Đáp án
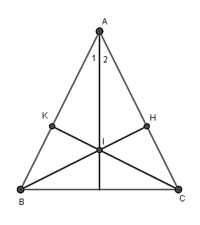
Xét hai tam giác AHB và AKC có :AB = AC ( gt )
Nên ΔAHB = ΔAKC ( cạnh huyền – cạnh góc nhọn )Suy ra AH = AK ( cạnh tương ứng )Xét hai tam giác vuông AHI và AKI ta có :AI là cạnh chungAH = AK
Nên ΔAHI = ΔAKI (cạnh huyền – cạnh góc vuông)
Xem thêm: Cách chứng minh đường trung trực lớp 7
A1 = A2 ( góc tương ứng bằng nhau )Do đó AI là tia phân giác góc ATrên đây VnDoc đã trình làng tới những bạn kim chỉ nan môn Toán học 7 : Các trường hợp bằng nhau của tam giác vuông. Để có hiệu quả cao hơn trong học tập, VnDoc xin ra mắt tới những bạn học viên tài liệu Chuyên đề Toán học 7, Giải bài tập Toán lớp 7, Giải VBT Toán lớp 7 mà VnDoc tổng hợp và ra mắt tới những bạn đọc
Video liên quan
Source: http://139.180.218.5
Category: tản mạn
