Có lẽ mục tiêu ở đây là giúp trẻ phân biệt được đâu là khối hộp CN, đâu là khối lập phương. Trẻ sẽ được học trải qua nhận ra trực quan, chưa sử dụng tới những khái niệm hay định nghĩa toán học .
Như vậy ta cần nắm được rõ mục tiêu của bài học kinh nghiệm là trẻ phân biệt được đâu là khối lập phương, đâu là khối hộp CN là thành công xuất sắc. Đáng tiếc là những bài tập cho học viên nó lại vô cùng “ phản toán học ” .
Bạn biết đấy, khối lập phương chỉ là một trường hợp đặc biệt của khối hộp chữ nhật, và đã là khối lập phương sẽ là khối hộp chữ nhật. Hãy quan sát ảnh dưới đây:
Bạn đang đọc: Khối hộp chữ nhật & khối lập phương -Toán lớp 1

Giả sử ở hình trên đầu, góc phải thì đáp án sẽ là 5 khối LP và 2 khối hộp CN. Rõ ràng câu vấn đáp này sai về mặt toán hoặc, đáp án đúng mực phải là 7 khối hộp CN, trong đó có 5 khối LP .
QC – Cộng + là một trong những cuốn sách phải đọc, càng sớm càng tốt. Ít nhất 850 người đã gửi phản hồi lại như vậy sau hơn 3.000 cuốn sách được bán ra. Xem trình làng và đặt mua tại đây. Bớt một bữa ăn để đổi lấy 1 thời cơ, đáng để thử lắm chứ ^ ^Người ta lý giải rằng học viên lớp 1 chưa hiểu được khối LP là 1 trường hợp của khối hộp CN nên phải rạch ròi để cách bé phân biệt. Theo HP đó chỉ là bao biện cho cách viết sách đi ngược lại triết lý toán học .
Chúng ta không cần dạy trẻ rằng khối LP vẫn là khối hộp CN quá sớm, nhưng chỉ cần tinh xảo một chút ít trong cách ra đề bài sẽ không gặp phải trường hợp trên :
Bài phía trên góc phải con HP đã ghi 7 Hộp CN, 5 LP lại bị gạch đi vì sai.
Chúng ta có những giải pháp đơn thuần hơn rất nhiều, để giúp trẻ phân biệt hình HCN vs LP, chỉ cần tuân thủ quy tắc sau :
Trong 1 hình có cả khối HCN và LP, chỉ hỏi có bao nhiêu khối LP. Trẻ đếm đúng mực số khối LP thực chất đã thỏa mãn nhu cầu nhu yếu phân biệt của tiềm năng bài học kinh nghiệm. Hỏi số hộp CN sẽ xảy ra thực trạng : Trẻ phải vấn đáp sai toán học để đúng với đáp án theo những gì được dạy .
Trong những hình lộn xộn, không chưa khối LP hoàn toàn có thể hỏi về số lượng khối hộp CN .
Đáng tiếc là những nhà biên soạn không nhìn ra điều cơ bản này, để trẻ phải vấn đáp sai cả toán học. Hãy nhìn một ví dụ đơn thuần hơn :

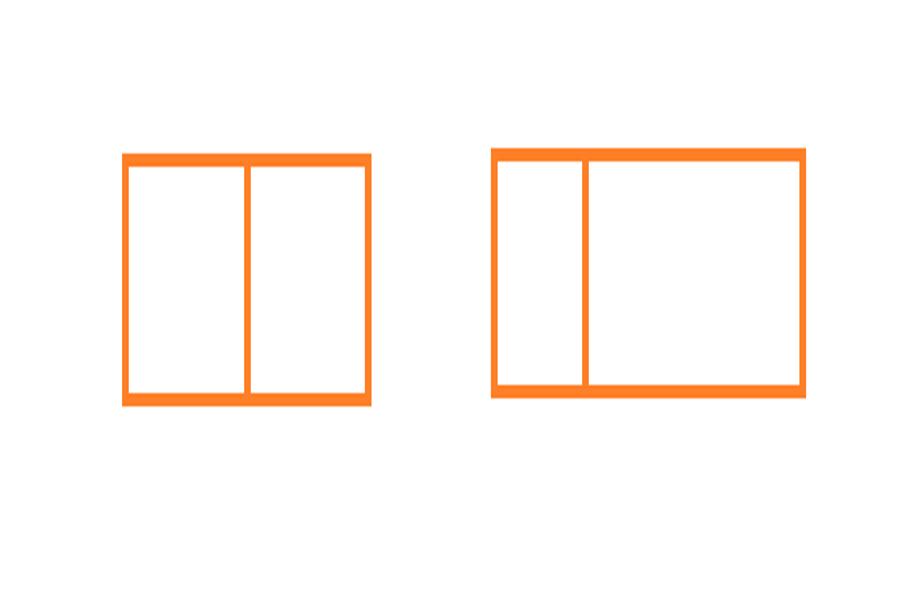
Nếu đề bài bên trái: Có bao nhiêu hình chữ nhật ở hình trên?
Xem thêm: Cuộc sống vốn luôn chứa đựng những muộn phiền, cũng may còn có bầu trời luôn cho ta niềm tin!
Tương tự như câu truyện khối LP phía trên, đây sẽ là một đề tài “ phản toán học ” cho trẻ lớp 1. Với kỹ năng và kiến thức được dạy, trẻ buộc phải vấn đáp đó là chỉ có 1 HCN ( 2 hình vuông vắn không được tính là HCN ). Trong khi đáp án thực tiễn phải là 3, cách ra đề “ thiếu tinh xảo ” đã khiến trẻ rơi vào trường hợp vấn đáp đúng thực chất sẽ sai theo ý của “ sách ”. Đối với hình này, câu hỏi chỉ nên là : Có bao nhiêu hình vuông vắn ?
Đối với hình bên phải, khi không sống sót hình vuông vắn trong HCN, thì hoàn toàn có thể hỏi gì cũng được. Có thể là số hình CN, số hình vuông vắn .
Rõ ràng tất cả chúng ta trọn vẹn có những cách để kiểm tra sự phân biệt của trẻ, nhưng lại không sai toán học. Sự tinh xảo là dẫn dắt trẻ đúng với kiến thức và kỹ năng trong tầm hiểu biết, nhưng không nên sai thực chất của yếu tố đi .
Source: http://139.180.218.5
Category: tản mạn