Giải chi tiết:

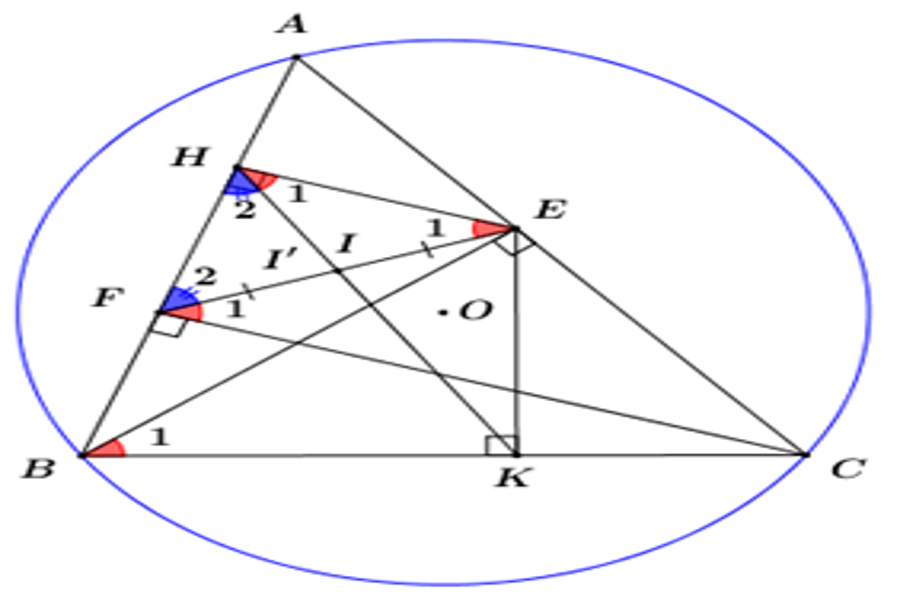
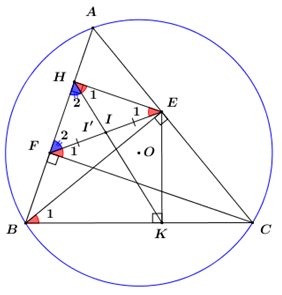
1) Chứng minh tứ giác BHEK là tứ giác nội tiếp.

Ta có:

\ ( \ angle BHE = { 90 ^ 0 } \ ) ( do \ ( EH \ bot AB \ ) )
\ ( \ angle BKE = { 90 ^ 0 } \ ) ( do \ ( EK \ bot BC \ ) )
Tứ giác \ ( BHEK \ ) có \ ( \ angle BHE + \ angle BKE = { 90 ^ 0 } + { 90 ^ 0 } = { 180 ^ 0 } \ ) nên là tứ giác nội tiếp ( tứ giác có tổng hai góc đối bằng \ ( { 180 ^ 0 } \ ) ) ( đpcm )

2) Chứng minh \(BH.BA = BK.BC\).

Theo câu a ) tứ giác \ ( BHEK \ ) nội tiếp nên \ ( \ angle BKH = \ angle BEH \ ) ( cùng chắn cung \ ( BH \ ) )
Ta có :
\ ( \ angle BEH + \ angle EBH = { 90 ^ 0 } \ ) ( do tam giác \ ( BHE \ ) vuông tại \ ( H \ ) ) .
\ ( \ angle BAE + \ angle EBH = { 90 ^ 0 } \ ) ( do tam giác \ ( ABE \ ) vuông tại \ ( E \ ) ) .
Nên \ ( \ angle BEH = \ angle BAE \ ) ( cùng phụ với \ ( \ angle EBH \ ) ) .
Mà \ ( \ angle BKH = \ angle BEH \ ) ( cmt ) nên \ ( \ angle BKH = \ angle BAE \, \, \, \ left ( { = \ angle BEH } \ right ) \ ) .
Xét \ ( \ Delta BHK \ ) và \ ( \ Delta BCA \ ) có :
\ ( \ angle ABC \ ) chung
\ ( \ angle BKH = \ angle BAE = \ angle BAC \ ) ( cmt )
\ ( \ Rightarrow \ Delta BHK \ sim \ Delta BCA \, \, \ left ( { g. g } \ right ) \ )
\ ( \ Rightarrow \ dfrac { { BH } } { { BC } } = \ dfrac { { BK } } { { BA } } \ ) ( hai cạnh tương ứng )

\( \Rightarrow BH.BA = BK.BC\) (đpcm).

3) Gọi F là chân đường vuông góc kẻ từ điểm C đến đường thẳng AB và I là trung điểm của đoạn thẳng EF. Chứng minh ba điểm H, I, K là ba điểm thẳng hàng.

Gọi \ ( I ‘ \ ) là giao điểm của HK và EF .
Xét tứ giác \ ( BFEC \ ) có : \ ( \ angle BFC = \ angle BEC = { 90 ^ 0 } \, \, \ left ( { gt } \ right ) \ ) nên là tứ giác nội tiếp ( tứ giác có hai đỉnh kề nhau cùng nhìn 1 cạnh những góc bằng nhau ) .
\ ( \ Rightarrow \ angle { B_1 } = \ angle { F_1 } \ ) ( hai góc nội tiếp cùng chắn cung \ ( EC \ ) ) .
Ta có : \ ( EH / / CF \ ) ( cùng vuông góc \ ( AB \ ) )
\ ( \ Rightarrow \ angle { F_1 } = \ angle { E_1 } \ ) ( so le trong )
Do đó \ ( \ angle { B_1 } = \ angle { E_1 } \ ) ( 1 ) .
Theo câu a, tứ giác \ ( BHEK \ ) nội tiếp nên \ ( \ angle { B_1 } = \ angle { H_1 } \ ) ( hai góc nội tiếp cùng chắn cung \ ( EK \ ) ) ( 2 ) .
Từ ( 1 ) và ( 2 ) suy ra \ ( \ angle { H_1 } = \ angle { E_1 } \ )
Tam giác \ ( I’HE \ ) có \ ( \ angle { H_1 } = \ angle { E_1 } \ ) nên là tam giác cân ( định nghĩa ) .
\ ( \ Rightarrow I’H = I’E \ ) ( đặc thù tam giác cân ) ( 3 )
Lại có :
\ ( \ angle { H_1 } + \ angle { H_2 } = \ angle BHE = { 90 ^ 0 } \ )
\ ( \ angle { F_2 } + \ angle { E_1 } = { 90 ^ 0 } \ ) ( do tam giác \ ( HEF \ ) vuông tại \ ( H \ ) ) .

Nên \(\angle {H_2} = \angle {F_2}\) hay tam giác \(I’HF\)  cân tại \(I’\) (định nghĩa).

\ ( \ Rightarrow I’H = I’F \ ) ( đặc thù tam giác cân ) ( 4 )
Từ ( 3 ) và ( 4 ) suy ra \ ( I’E = I’F \ ) hay \ ( I ‘ \ ) là trung điểm của \ ( EF \ ) .
Do đó \ ( I ‘ \ equiv I \ ) nên ba điểm \ ( H, I, K \ ) thẳng hàng ( đpcm ).

Source: http://139.180.218.5
Category: tản mạn