Hình trụ là gì? Công thức tính diện tích, diện tích xung quanh và thể tích hình trụ là gì? Hình trụ thuộc dạng hình khối nào? Cùng tìm hiểu các kiến thức về hình trụ qua bài viết sau.

Nội dung chính [ẩn đi]
Hình trụ là gì?
Định nghĩa hình trụ:
- Hình trụ là hình có hai mặt đáy là hình bằng nhau và song song với nhau.
- Hình trụ được gọi bằng cái tên đầy đủ hơn là hình trụ tròn
- Hình trụ tiếng Anh là Cylinder

Lưu ý:
- Chỉ có lăng trụ tam giác chứ không có khái niệm hình trụ tam giác
- Chỉ có hình lập phương chứ không có hình trụ vuông
Hình trụ có phải là một khối tròn xoay?
Hình trụ là một khối tròn xoay
Khối tròn xoay là một khối hình được tạo ra bằng cách quay một mặt phẳng quanh một trục cố định.
Bạn đang đọc: Công thức tính diện tích, thể tích hình trụ như thế nào?
Một số khối tròn xoay được học trong chương trình đại trà phổ thông là : Hình trụ, hình nón, hình cầu hay còn gọi là hình trụ tròn xoay, hình nón tròn xoay, hình cầu tròn xoay
Các công thức tính diện tích hình trụ
Diện tích xung quanh hình trụ
Diện tích xung quanh của hình trụ bằng tích 2 lần nửa đường kính hình trụ với chiều cao và số pi .
Công thức tính diện tích quy hoạnh xung quanh của hình trụ :
Sxq= 2.π.r.h (m2)
Trong đó
- Sxq là diện tích xung quanh của hình trụ
- r: Bán kính đường tròn đáy
- h: Chiều cao
Diện tích toàn phần hình trụ
Diện tích toàn phần hình trụ bằng tổng diện tích quy hoạnh xung quanh và diện tích quy hoạnh hai mặt dưới .
Stp= Sxq+S2đáy = 2.π.r.h + 2π.r2= 2π.r.(r+h) (m2)
Trong đó :
- Sxq, Stp : Lần lượt là diện tích xung quanh và diện tích toàn phần của hình trụ
- S2đáy: Diện tích hai đáy của hình trụ
- r: Bán kính đường tròn đáy
- h: Chiều cao
Công thức tính thể tích hình trụ
Thể tích hình trụ
Thể tích hình trụ bằng tích độ cao với bình phương nửa đường kính hình tròn trụ mặt dưới và số pi. Hoặc thể tích hình trụ bằng diện tích quy hoạnh dưới mặt đáy nhân với chiều cao .
Công thức tính thể tính hình trụ :
V = Sđáy.h = π.r2.h (m3)
Trong đó :
- V là thể tích hình trụ
- Sđáy là diện tích mặt đáy
- r là bán kính hình tròn đáy
- h là chiều cao hình trụ
- π là số pi, có giá trị bằng 3,14
Tìm bán kính đáy hình trụ
Tìm nửa đường kính đáy hình trụ bằng cách xác lập nửa đường kính của một hình tròn trụ bất kể cắt ngang hình trụ và vuông góc với chiều cao. Mọi hình tròn trụ được như vậy đều có nửa đường kính bằng với mặt dưới. Có thể tìm được nửa đường kính đáy hình trụ bằng những chiêu thức sau :
Đo đường kính mặt dưới rồi chia cho 2, bởi R = 2 r
Nếu biết chu vi hình tròn trụ đáy thì bạn chia cho 2 π, bởi C = 2 πr
Công thức tính bán kính đáy: r = ½ R
Tính diện tích đáy hình trụ
Khi biết được giá trị của nửa đường kính đáy hình trụ, ta tính được diện tích quy hoạnh đáy hình trụ theo công thức sau :
Diện tích đáy hình trụ: Sđáy = π.r.2 (m2)
Tính chiều cao hình trụ
Chiều cao hình trụ được chính là đoạn thẳng nối hai đáy và vuông góc với đáy hình trụ. Như vậy có vô số đoạn thẳng là chiều cao của hình trụ, trong đó có 2 vị trí quan mà ta hoàn toàn có thể xác lập chiều cao thuận tiện :
- Đoạn thẳng nối tâm hai hình tròn đáy của hình trụ
- Đoạn thẳng nối một điểm trên đường tròn đáy và hình chiếu của nó trên hình tròn đáy còn lại của hình trụ
Bằng cách đặt thước vuông góc với dưới mặt đáy hình trụ và đọc số đo của thước ở dưới mặt đáy còn lại là biết được giá trị của chiều cao của hình trụ .
Các dạng bài tập liên quan tới tính thể tích hình trụ
Bài 1: Cho bán kính đáy và chiều cao, tính thể tích khối trụ
Cho hình trụ có đáy là hình tròn trụ ngoại tiếp tam giác đều cạnh a. Chiều cao khối trụ bằng 3 a. Tính thể tích khối trụ đã cho .
Giải:
Bán kính đáy của khối trụ là :
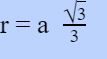
Thể tích của khối trụ đã cho là :
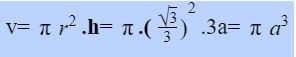
Bài 2: Cho thể tích khối trụ và chiều cao, tính bán kính đáy
Cho hình trụ có chiều cao 2 a, thể tích bằng πa³. Tính nửa đường kính đáy của hình trụ .
Giải :
Áp dụng công thức ta có :
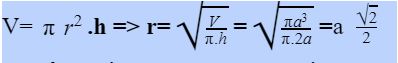
Bài 3: Cho thể tích khối trụ, tính bán kính đáy và chiều cao
Cho hình trụ có chu vi một đáy là C = 2 π và thể tích V = 12 π. Chiều cao của hình trụ là bao nhiêu ?
Giải :
Bán kính đáy của hình trụ là r =C / 2π = 1
Chiều cao của hình trụ bằng h= V / (π. r2 ) = 12π / (π. 12) = 12
Bài 4: Tính thể tích hình trụ tròn khi biết độ dài dây cung, góc và khoảng cách giữa dây cung với trục
Cho hình trụ ( H ) có 2 đáy là những đường tròn tâm O và O ’. Điểm A, B lần lượt nằm trên đường tròn ( O ), ( O ’ ). Biết AB = a, AB tạo với trục OO ’ góc α. Khoảng cách giữa OO ’ và AB bằng d. Tính theo a và α thể tích hình trụ ( H ) .
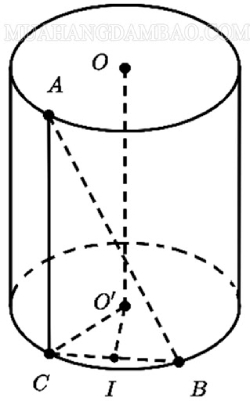
Gọi C là hình chiếu của A lên đường tròn (O’). Gọi I là trung điểm của BC. Dễ thấy góc BAC là góc giữa dây AB và trục OO’. Tức là góc BAC = α.
Chiều cao khối trụ đã cho là h = OO ’ = AB cosα = a cosα
IC = ½ BC = a. sinα
O’I = d là khoảng cách giữa AB và OO ’
Nên nửa đường kính đáy khối trụ là :
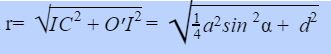
Vậy thể tích khối trụ là :
![]()
Một số bài toán áp dụng tính thể tích hình trụ
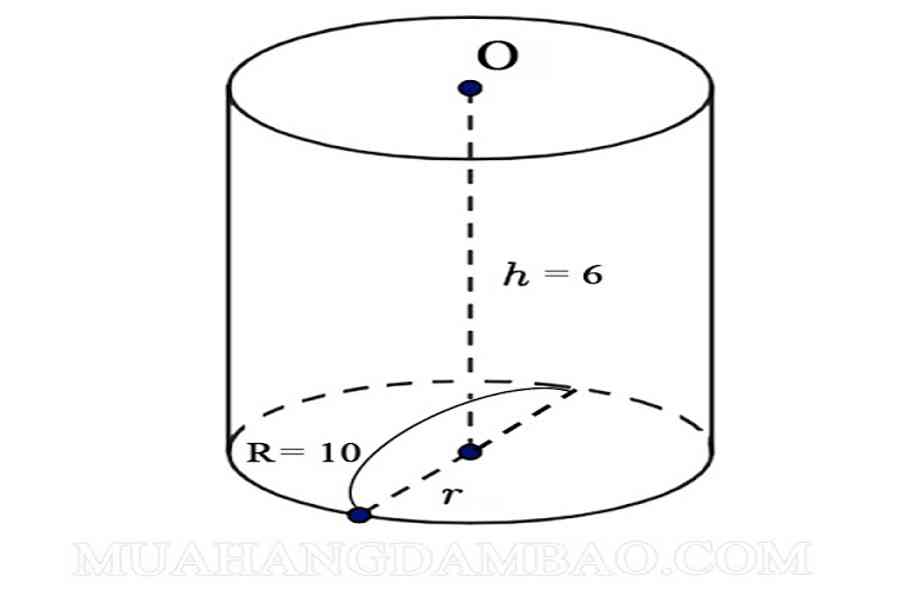
Bài 1: Tính diện tích toàn phần của hình trụ, có độ dài đường tròn đáy là 10cm, khoảng cách giữa 2 đáy là 6cm.
Bài giải :
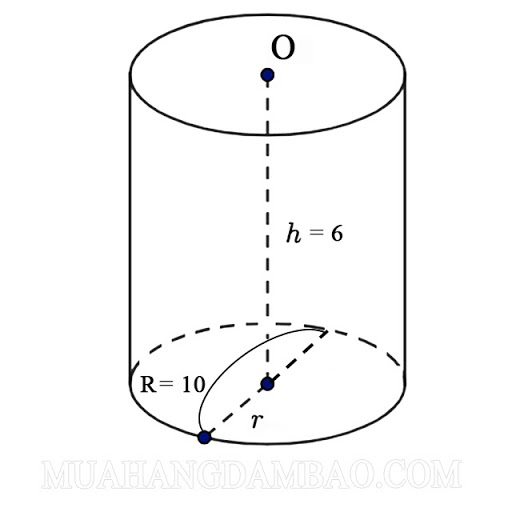
Ta có : h = 6 cm, R = 10 cm => r = 5 cm
Áp dụng công thức tính diện tích quy hoạnh toàn phần hình trụ :
Stp = 2 πr. ( r + h ) = 2.5 ( 5 + 6 ) = 110 ( cm2 )
Vậy diện tích quy hoạnh hình trụ là 110 ( cm2 )
Bài 2: Tính diện tích toàn phần của hình trụ có chiều cao là 7cm và diện tích xung quanh bằng 310 cm2
Bài giải

Theo đề bài ta có h = 7, Sxq = 310 cm2
Áp dụng công thức tính diện tích quy hoạnh xung quanh Sxq = 2 πr. h
=> r = Sxq / 2 πr. h = 310 / 2 πr. 7 = 7 cm
Vậy Sđáy = π. r2 = π. 72 = 49 π = 154 ( cm2 )
=> Diện tích toàn phần của khối trụ là
Stp = 2. Sđáy + Sxq = 2.154 + 310 = 618 cm2
Bài 3: Một hình trụ có chu vi đáy 30 cm và chiều cao là 10cm. Tính thể tích hình trụ?
Bài giải :
Bán kính đáy hình trụ là : r = C / 2 π = 30 / ( 2.3,14 ) = 4,78 cm
V hình trụ = Sđáy. h = π. r2. h = 717,44 ( cm3 )
Đáp số : 717,44 ( cm3 )
Bài 4: Tính thể tích hình trụ bên dưới, biết: r = 3 cm, AC = 5 cm.
Bài giải
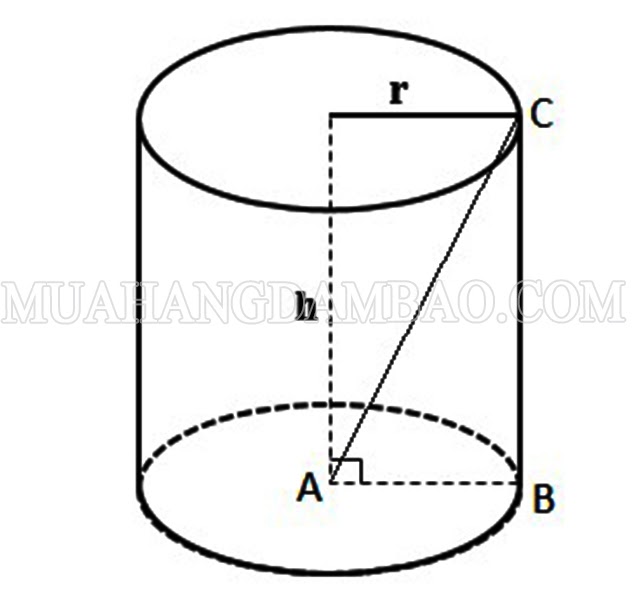
– Tính chiều cao hình trụ :
Xét tam giác vuông ABC, ta có :
AB = r = 3 cm
BC = h
BC2 = AC2 – AB2 = 52 – 32 = 16
=> BC = 4 cm
=> h = 4 cm
– Tính diện tích quy hoạnh đáy hình trụ :
Sđáy = π. r2 = 28,26 ( cm2 )
=> V hình trụ ở trên là: V = Sđáy.h = 28,26.4 = 113,04 (cm3)
Hãy linh động tư duy để vận dụng tổng thể những công thức đã có sẵn trên đây để xử lý những bài toán tương quan để thể tích và diện tích quy hoạnh hình trụ nhé
Source: http://139.180.218.5
Category: tản mạn