Nội dung chính
Tính chất của trọng tâm và cách xác định trọng tâm tam giác trong Hình học
Tính chất của trọng tâm và cách xác định trọng tâm trong Hình học
Như các bạn đã biết giao điểm của ba đường trung tuyến trong một tam giác chính là trọng tâm của tam giác đó, vậy chúng là điểm như thế nào và có những tính chất đặc biệt gì. Hãy cùng chúng tôi tìm hiểu nhé!
I. Lý thuyết về trọng tâm
1. Trọng tâm là gì?
Trọng tâm trong tam giác là giao điểm của ba đường trung tuyến xuất phát từ ba đỉnh.
Cho tam giác ABC, trong đó AM, BN, CP lần lượt là trung tuyến của tam giác xuất phát từ đỉnh A, B, C. AM, BN, CP cắt nhau tại G nên G chính là trọng tâm của tam giác
Công thức liên quan:
2. Tính chất trọng tâm của tam giác
Để xác định trọng tâm của một tam giác ta triển khai : Cách 1 :
- Tìm trung điểm M của BC sao cho MC = MB
- Nối A với M ta được đường trung tuyến AM.
- Tương tự với các đường trung tuyến còn lại.
- Giao 3 đường trung tuyến là điểm G. Suy ra G chính là trọng tâm tam giác ABC.
Cách 2 :
- Tìm trung điểm M của BC sao cho MC = MB
- Nối A với M ta được đường trung tuyến AM.
- Trên đoạn thẳng AM lấy điểm G sao cho: \ ( AG = \ dfrac { 2 } { 3 } AM \ )
- Vậy theo tính chất trọng tâm ta có G chính là trọng tâm tam giác ABC.
Cho tam giác ABC có AM, BN, CP lần lượt là ba đường trung tuyến tại đỉnh A, B, C. Ta có giao của ba đường trung tuyến là điểm G. Vậy G là trọng tâm của tam giác ABC.
Ta có tính chất:
\ ( \ overrightarrow { AG } = \ dfrac { 2 } { 3 } \ overrightarrow { AM } \ Rightarrow AG = \ dfrac { 2 } { 3 } AM \ ) \ ( \ overrightarrow { GA } + \ overrightarrow { GB } + \ overrightarrow { GC } = \ overrightarrow { 0 } \ )
II. Trọng tâm của các hình học đặc biệt
- Trọng tâm tam giác vuông
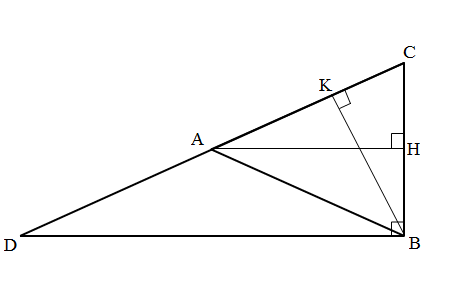
Tam giác ABC vuông tại B, từ B vẽ đường trung tuyến BA, vì BA là đường trung tuyến của góc vuông nên : BA = 50% CD = AD = AC. Vậy tam giác ADB và tam giaisc ABC lần lượt cân tại A,
- Trọng tâm tam giác cân
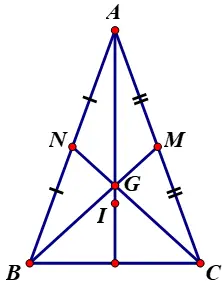
Cho tam giác ABc cân tại A, G là trọng tâm tam giác ABC. Vì tam giác cân tại A, nên AG vừa là đường trung tuyến, vừa là đường cao và là đường phân giác cùa tam giác ABC. Hệ quả :
– \(\widehat{BAG}=\widehat {CAG}\)
– AG vuông góc với BC.
- Trọng tâm tam giác đều là gì
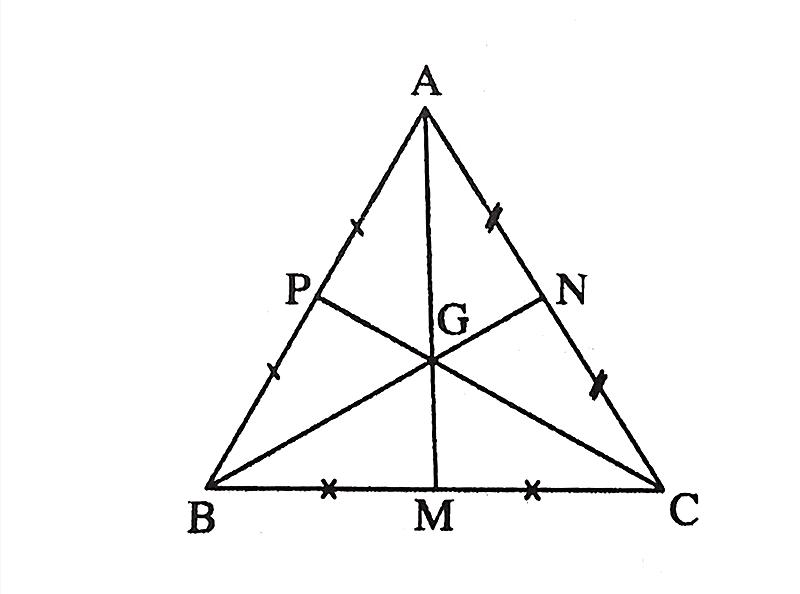
Cho tam giác ABC đều, G là giao điểm ba đường trung tuyến. Theo đặc thù của tam giác đều ta có G vừa là trọng tâm, trựa tâm, tâm đường tròn ngoại tiếp và nội tiếp của tam giác ABC.
- Trọng tâm tứ diện
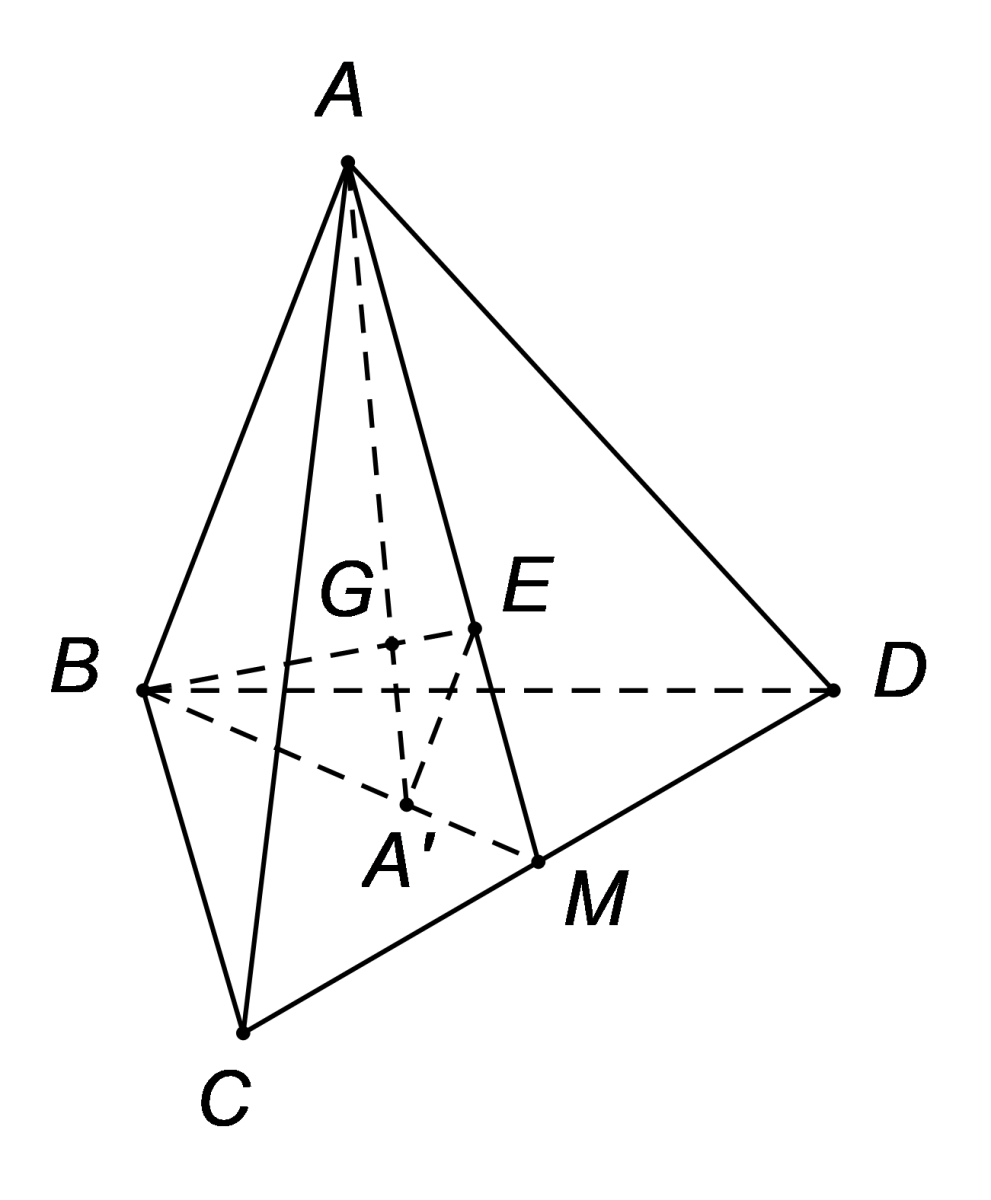
Ta có G là trọng tâm tứ diện ABCD. Trọng tâm tứ diện là giao điểm của bốn đường thẳng nối đỉnh và trọng tâm của tam giác đối lập.
III. Luyện tập
Bài tập: Cho tam giác ABC, trung tuyến BM = CN. BM cắt CN tại G. CHứng minh tam giác ABC cân tại A
Lời giải : Vì BM và CN là hai đường TT của tam giác mà BM giao CN tại G, nên ta có : \ ( \ dfrac { BG } { BM } = \ dfrac { CG } { CN } = \ dfrac { 2 } { 3 } \ ) Mà BM = CN nên BG = CN và GN = GM Xét \ ( \ Delta BNG \ và \ \ Delta CGM \ ) ta có : BG = CN GN = GM \ ( \ widehat { BGN } = \ widehat { CGM } \ ) ( 2 goc đối đỉnh ) Suy ra : \ ( \ Delta BNG \ đồng \ dạng \ \ Delta CMG \ ) Suy ra : BN = CM ( 1 ) mà M và N lần lượt là trung điểm của AB và AC ( 2 ) Từ ( 1 ) và ( 2 ) ta cí AB = AC => Tam giác ABC cân tại A ( đpcm ).
Tham khảo bộ công thức cực chất >>>>Toàn bộ công thức siêu nhanh Toán 12 đầy đủ nhất từ A – Z ôn thi THPTQG
Xem thêm: Cuộc sống vốn luôn chứa đựng những muộn phiền, cũng may còn có bầu trời luôn cho ta niềm tin!
Vậy là chúng ta đã tìm hiểu xong về khái niệm trọng tâm. Nếu có thắc mắc và ý kiến thú vị xin vui lòng để lại dưới mục bình luận nhé, chúng tôi rất mong nhận được sự đóng góp từ các bạn!
Source: http://139.180.218.5
Category: tản mạn
