Chân trời (hoặc đường chân trời) là một đường có thể nhìn thấy rõ ràng phân cách mặt đất với bầu trời.. Khi đứng từ bờ và nhìn ra biển thì vùng biển gần đường chân trời được gọi là khơi.[1][2] Trong tiếng Anh, từ horizon có nguồn gốc từ tiếng Hy Lạp “ὁρίζων κύκλος” (horizōn kyklos), “vòng tròn chia cắt”,[3] từ động từ “ὁρίζω” (horizō), “chia, tách”,[4] và từ “ὅρος” (Oros), ” ranh giới, mốc”.[5]
Hình thức và ứng dụng.
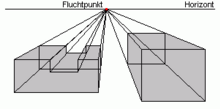 Chân trời trong phép chiếu phối cảnh .
Chân trời trong phép chiếu phối cảnh .
Trước khi loài người phát minh ra đài phát thanh và điện báo thì khoảng cách tới chân trời có thể nhìn thấy ở trên biển là cực kỳ quan trọng vì nó thể hiện phạm vi tối đa có thể truyền tin và tầm nhìn. Thậm chí ngày nay, khi điều khiển một chiếc máy bay theo quy tắc VFR (Vision flight rules), là tập hợp những quy tắc hướng dẫn phi công điều khiển máy bay trong điều kiện thời tiết cho phép có thể dùng mắt thường định vị vị trí, đường đi, né tránh chướng ngại vật của máy bay, thì phi công cũng sử dụng các mối quan hệ trực quan giữa mũi của máy bay và đường chân trời để điều khiển máy bay. Một phi công cũng có thể dựa vào đường chân trời để định hướng không gian.
Bạn đang đọc: Chân trời.
Trong nhiều nghành nghề dịch vụ, đặc biệt quan trọng là phép chiếu phối cảnh trong những bản vẽ, thì độ cong của Trái Đất được bỏ lỡ và chân trời được xem là một đường thẳng triết lý mà toàn bộ những điểm trên bất kể mặt phẳng nằm ngang nào cũng đều quy tụ về đó ( khi chiếu lên mặt phẳng hình ảnh ) làm tăng khoảng cách từ người quan sát ( làm cho người quan sát cảm thấy được độ xa gần của hình ảnh chiếu 3D ) .Trong thiên văn học, chân trời là mặt phẳng nằm ngang qua mắt của người quan sát. Nó là mặt phẳng cơ bản của hệ tọa độ chân trời và là quỹ tích những điểm có độ cao 0 độ .
Khoảng cách đến chân trời.
Bỏ qua ảnh hưởng tác động của sự khúc xạ trong khí quyển, thì khoảng cách từ 1 người quan sát trên mặt đất đến chân trời, là khoảng chừng : [ 6 ]
- d ≈ 3.57 h, { \ displaystyle d \ approx 3.57 { \ sqrt { h } } \, , }
trong đó, d tính bằng km, h là độ cao so với mực nước biển tính bằng m.
Ví dụ :
- Đối với một người quan sát đứng trên mặt đất với h=1.70m (5 ft 7in), đường chân trời ở khoảng cách 4.7 km (2.9 dặm).
- Đối với một người quan sát đứng trên mặt đất với h = 2 m (6 ft 7 in), đường chân trời ở khoảng cách 5 km (3.1 dặm).
- Đối với một người quan sát đứng trên một ngọn đồi hoặc tháp cao 100 mét (330 ft), đường chân trời ở khoảng cách 39 km (24 dặm).
- Đối với một người quan sát đứng ở đỉnh của tòa nhà Burj Khalifa cao 828 mét (2.717 ft), đường chân trời ở khoảng cách 111 km (69 dặm).
Với d tính bằng dặm,[7] h tính bằng feet, thì
- d ≈ 1.22 h. { \ displaystyle d \ approx 1.22 { \ sqrt { h } } \ ,. }
Công thức hình học.
 Công thức cát tuyến và tiếp tuyến của đường tròn .
Công thức cát tuyến và tiếp tuyến của đường tròn . Ba loại chân trời .Nếu giả định Trái Đất là một hình cầu không có khí quyển thì ta hoàn toàn có thể thuận tiện tính ra khoảng cách từ người quan sát tới chân trời. ( Bán kính cong của Trái Đất thực sự đổi khác 1 %, do đó công thức này là không đúng mực thậm chí còn đã giả sử là không có sự khúc xạ. ) Theo công thức liên hệ giữa tiếp tuyến và cát tuyến trong đường tròn, ta có :
Ba loại chân trời .Nếu giả định Trái Đất là một hình cầu không có khí quyển thì ta hoàn toàn có thể thuận tiện tính ra khoảng cách từ người quan sát tới chân trời. ( Bán kính cong của Trái Đất thực sự đổi khác 1 %, do đó công thức này là không đúng mực thậm chí còn đã giả sử là không có sự khúc xạ. ) Theo công thức liên hệ giữa tiếp tuyến và cát tuyến trong đường tròn, ta có :
- O C 2 = O A × O B. { \ displaystyle \ mathrm { OC } ^ { 2 } = \ mathrm { OA } \ times \ mathrm { OB } \ ,. }
Trong đó :
- d = OC = khoảng cách đến chân trời
- D = AB = đường kính của Trái Đất
- h = OB = độ cao của người quan sát so với mực nước biển.
- D+h = OA = đường kính + độ cao người quan sát.
Phương trình trở thành :
- d 2 = h ( D + h ) { \ displaystyle d ^ { 2 } = h ( D + h ) \, \ ! }
hoặc
- d = h ( D + h ) = h ( 2 R + h ), { \ displaystyle d = { \ sqrt { h ( D + h ) } } = { \ sqrt { h ( 2R + h ) } } \, , }
R là bán kính Trái Đất.
Ta cũng hoàn toàn có thể sử dụng định lý Pythagore trong trường hợp này để tính khoảng cách đến chân trời. Do tia nhìn của người quan sát tiếp tuyến với đường tròn Trái Đất vì vậy nó vuông góc với nửa đường kính tại điểm tiếp xúc, tạo nên 1 tam giác vuông với cạnh huyền là tổng nửa đường kính với độ cao của người quan sát so với mực nước biển. Với :
- d = khoảng cách đến đường chân trời
- h = chiều cao của người quan sát so với mực nước biển
- R = bán kính của Trái Đất
Theo định lý Pythagore, ta có :
- ( R + h ) 2 = R 2 + d 2 { \ displaystyle ( R + h ) ^ { 2 } = R ^ { 2 } + d ^ { 2 } \, \ ! }
- R 2 + 2 R h + h 2 = R 2 + d 2 { \ displaystyle R ^ { 2 } + 2R h + h ^ { 2 } = R ^ { 2 } + d ^ { 2 } \, \ ! }
- d = h ( 2 R + h ). { \ displaystyle d = { \ sqrt { h ( 2R + h ) } } \ ,. }
Một phương trình thể hiện sự tương quan giữa độ dài cung tròn s với góc mở γ tính bằng radian:
- s = R γ ; { \ displaystyle s = R \ gamma \, ; }
mà :
- cos γ = cos s R = R R + h. { \ displaystyle \ cos \ gamma = \ cos { \ frac { s } { R } } = { \ frac { R } { R + h } } \ ,. }
Thế vào, ta có :
- s = R cos − 1 R R + h. { \ displaystyle s = R \ cos ^ { – 1 } { \ frac { R } { R + h } } \ ,. }
Lại có :
- tan γ = d R ; { \ displaystyle \ tan \ gamma = { \ frac { d } { R } } \, ; }
Thế vào phương trình trên:
Xem thêm: Khuông nhạc.
- s = R tan − 1 d R. { \ displaystyle s = R \ tan ^ { – 1 } { \ frac { d } { R } } \ ,. }
Khoảng cách d và độ dài cung tròn s là gần bằng nhau vì độ cao h rất bé so với bán kính R (h ≪ R)
Những công thức hình học gần đúng.
Nếu người quan sát đứng ở vị trí gần với mặt đất, thì độ cao h trong tham số (2R + h) có thể bỏ qua, khi đó công thức trở thành:
- d = 2 R h. { \ displaystyle d = { \ sqrt { 2R h } } \ ,. }
Với giá trị của nửa đường kính Trái Đất là 6371 km thì khoảng cách đến đường chân trời là :
- d ≈ 12.74 h ≈ 3.57 h, { \ displaystyle d \ approx { \ sqrt { 12.74 h } } \ approx 3.57 { \ sqrt { h } } \, , }
với d được tính bằng km, h là độ cao tính từ mực nước biển đến mắt của người quan sát với đơn vị đo lường là mét.
Nếu sử dụng hệ thống đơn vị của Anh, thì khoảng cách đến đường chân trời là:
- d ≈ 1.50 h ≈ 1.22 h, { \ displaystyle d \ approx { \ sqrt { 1.50 h } } \ approx 1.22 { \ sqrt { h } } \, , }
với d tính bằng dặm, h tính bằng feet.
Những công thức trên được sử dụng khi độ cao h rất bé nếu so với bán kính Trái Đất (6.371 km), kể cả khi người quan sát đứng ở trên 1 đỉnh núi, trên máy bay hoặc khinh khí cầu. Với các hằng số đã xác lập thì những công thức này có sai số trong phạm vi khoảng 1%.
Công thức tính đúng mực với giả định Trái Đất là hình cầu.
Nếu độ cao h là đáng kể so với bán kính R, như khi quan sát từ các vệ tinh, thì cần phải có công thức tính chính xác:
- d = 2 R h + h 2, { \ displaystyle d = { \ sqrt { 2R h + h ^ { 2 } } } \, , }
Với R là bán kính Trái Đất (R và h phải tính cùng 1 đơn vị đo lường. Ví dụ, nếu vị tinh ở độ cao 2000 km, thì khoảng cách đến đường chân trời là 5.430 kilômét (3.370 mi); nếu ta bỏ qua tham số h thì sẽ cho 1 kết quả là 5.048 kilômét (3.137 mi) với sai số lên đến 7%.
Những đối tượng người dùng quan sát được ở trên đường chân trời.
 Khoảng cách hình học đến đường chân trờiĐể giám sát chiều cao của một đối tượng người dùng hoàn toàn có thể nhìn thấy trên đường chân trời, với giả thuyết đối tượng người dùng quan sát được là đỉnh của một vật thể thì ta tính được khoảng cách từ đỉnh đó đến đường chân trời, sau đó thêm hiệu quả này vào khoảng cách từ người quan sát đến đường chân trời. Ví dụ, một người quan sát với chiều cao 1,70 m đứng trên mặt đất, khoảng cách từ người đó đến đường chân trời là 4,65 km. Đối với một tháp với chiều cao 100 m, khoảng cách từ đỉnh tháp đến đường chân trời là 35,7 km. Vì vậy, một người quan sát trên một bãi biển hoàn toàn có thể nhìn thấy tháp miễn là nó cách người quan sát không xa hơn 40,35 km. Ngược lại, nếu một người quan sát trên một chiếc thuyền ( h = 1,7 m ) chỉ hoàn toàn có thể nhìn thấy ngọn cây cao 10 m trên một bờ biển gần đó nếu cây này cách người quan sát trong khoảng chừng 16 km. Theo hình bên phải, người trên thuyền chỉ hoàn toàn có thể nhìn thấy được ngọn hải đăng nếu như :
Khoảng cách hình học đến đường chân trờiĐể giám sát chiều cao của một đối tượng người dùng hoàn toàn có thể nhìn thấy trên đường chân trời, với giả thuyết đối tượng người dùng quan sát được là đỉnh của một vật thể thì ta tính được khoảng cách từ đỉnh đó đến đường chân trời, sau đó thêm hiệu quả này vào khoảng cách từ người quan sát đến đường chân trời. Ví dụ, một người quan sát với chiều cao 1,70 m đứng trên mặt đất, khoảng cách từ người đó đến đường chân trời là 4,65 km. Đối với một tháp với chiều cao 100 m, khoảng cách từ đỉnh tháp đến đường chân trời là 35,7 km. Vì vậy, một người quan sát trên một bãi biển hoàn toàn có thể nhìn thấy tháp miễn là nó cách người quan sát không xa hơn 40,35 km. Ngược lại, nếu một người quan sát trên một chiếc thuyền ( h = 1,7 m ) chỉ hoàn toàn có thể nhìn thấy ngọn cây cao 10 m trên một bờ biển gần đó nếu cây này cách người quan sát trong khoảng chừng 16 km. Theo hình bên phải, người trên thuyền chỉ hoàn toàn có thể nhìn thấy được ngọn hải đăng nếu như :
- D B L < 3.57 ( h B + h L ), { \ displaystyle D_ { \ mathrm { BL } } <3. 57 \, ( { \ sqrt { h_ { \ mathrm { B } } } } + { \ sqrt { h_ { \ mathrm { L } } } } ) \, , }
với DBL tính bằng km, hB và hL tính bằng m. Nếu không bỏ qua khúc xạ khí quyển, thì điều kiện về tầm nhìn trở thành:
- D B L < 3.86 ( h B + h L ). { \ displaystyle D_ { \ mathrm { BL } } <3. 86 \, ( { \ sqrt { h_ { \ mathrm { B } } } } + { \ sqrt { h_ { \ mathrm { L } } } } ) \ ,. }
Ảnh hưởng của sự khúc xạ khí quyển.
Do những tia sáng bị khúc xạ khí quyển, nên khoảng cách thực tiễn của đường chân trời thấy được ( tầm nhìn ) sẽ lớn hơn khoảng cách đo lường và thống kê với công thức hình học. Với những điều kiện kèm theo tiêu chuẩn của khí quyển, sự xô lệch là khoảng chừng 8 %, tuy nhiên, sự khúc xạ bị ảnh hưởng tác động bởi gradient nhiệt độ, biến hóa đáng kể hàng ngày, đặc biệt quan trọng là trên mặt nước, do đó, giá trị đo lường và thống kê cho sự khúc xạ chỉ xê dịch. [ 6 ]
Phương pháp chính xác – Sweer
Khoảng cách d đến đường chân trời được tính bằng công thức:[8]
- d = R E ( ψ + δ ), { \ displaystyle d = { { R } _ { \ text { E } } } \ left ( \ psi + \ delta \ right ) \, , }
với RE là bán kính Trái Đất, ψ là độ nghiêng (võng) của đường chân trời và δ là độ khúc xạ của đường chân trời.
Độ nghiêng được tính thuận tiện bằng công thức :
- cos ψ = R E μ 0 ( R E + h ) μ, { \ displaystyle \ cos \ psi = { \ frac { { { R } _ { \ text { E } } } { { \ mu } _ { 0 } } } { \ left ( { { R } _ { \ text { E } } } + h \ right ) \ mu } } \, , }
với h là độ cao của người quan sát so với mặt đất, μ là chỉ số khúc xạ của không khí ở độ cao của người quan sát, và μ0 là chỉ số khúc xạ của không khí ở bề mặt Trái Đất.
Độ khúc xạ δ của đường chân trời tính bằng công thức:
- δ = − ∫ 0 h tan ϕ d μ μ, { \ displaystyle \ delta = – \ int _ { 0 } ^ { h } { \ tan \ phi { \ frac { { \ text { d } } \ mu } { \ mu } } } \, , }
với
ϕ
{\displaystyle \phi \,\!}

ϕ
{\displaystyle \phi \,\!}
tương quan với nhau theo công thức:
- ϕ = 90 ∘ − ψ. { \ displaystyle \ phi = 90 { } ^ { \ circ } – \ psi \ ,. }
Phương pháp gần đúng—Young
Có thể tính gần đúng bằng công thức đơn giản hơn sử dụng R′ = 7/6 RE. Khoảng cách đến đường chân trời là:[6]
- d = 2 R ′ h. { \ displaystyle d = { \ sqrt { 2R ^ { \ prime } h } } \ ,. }
Lấy bán kính Trái Đất là 6371 km, với d tính bằng km và h tính bằng m,
-
d
≈
3.86h
;
{\displaystyle d\approx 3.86{\sqrt {h}}\,;}
với d tính bằng dặm và h tính bằng feet,
- d ≈ 1.32 h. { \ displaystyle d \ approx 1.32 { \ sqrt { h } } \ ,. }
Kết quả tính bằng giải pháp Young gần đúng với tác dụng từ giải pháp Sweer, với sai số hoàn toàn có thể đồng ý được .
Liên kết ngoài.
Source: http://139.180.218.5
Category: Kiến thức âm nhạc


























