Xem thêm các sách tham khảo liên quan:

Xác suất của biến cố –
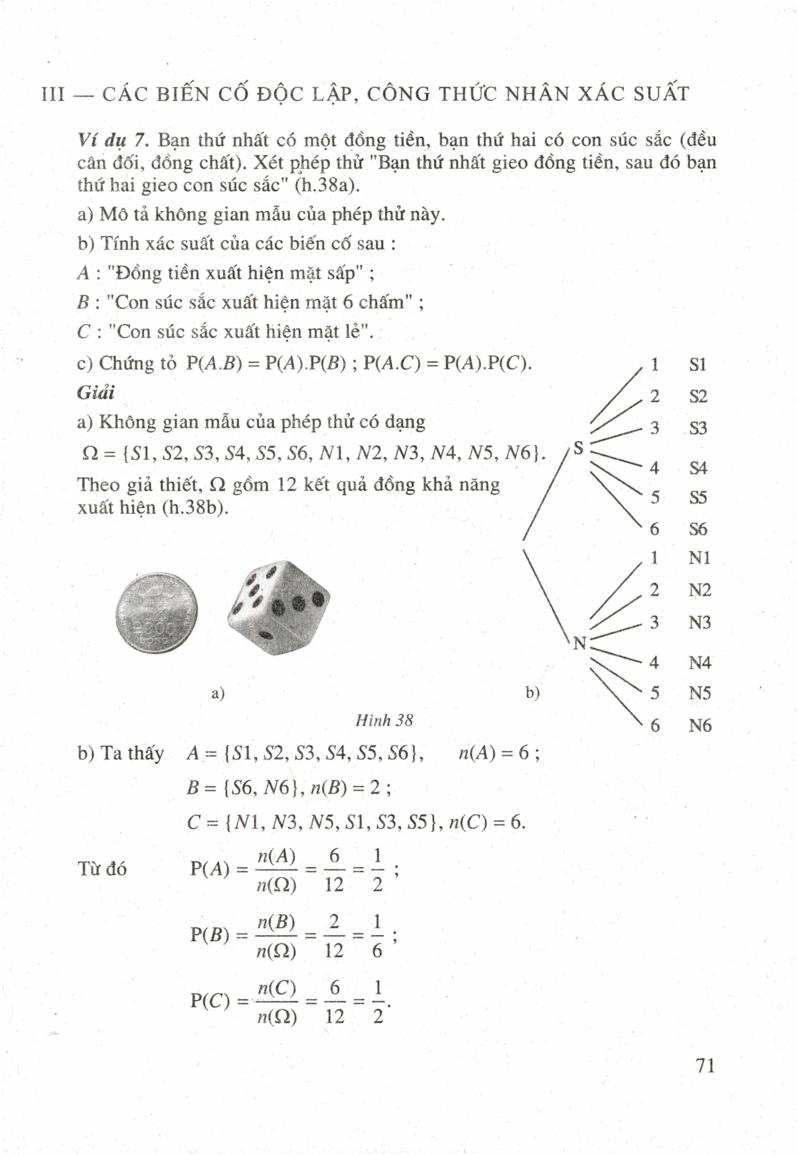
Một đặc trưng định tính quan trọng của biến cố tương quan đến một phép thử là nó hoàn toàn có thể xảy ra hoặc không xảy ra khi phép thử đó được triển khai. Một câu hỏi được đặt ra là nó có xảy ra không ? Khả năng xảy ra của nó là bao nhiêu ? Như vậy, phát sinh một yếu tố là cần phải gắn cho biến cố đó một số lượng phải chăng để nhìn nhận năng lực xảy ra của nó. Ta gọi số đó là xác suất của biến cố. Ví dụ I. Gieo ngẫu nhiên một con súc sắc cân đối và đồng chất. Các tác dụng hoàn toàn có thể là ( h. 33 ) o “. … : : : :: Hình 33 Không gian mẫu của phép thử này có sáu thành phần, được diễn đạt như sau ( ) = { 1,2,3,4,5,6 }. Do con súc sắc là cân đối, đồng chất và được gieo ngẫu nhiên nên năng lực Open từng mặt của con súc sắc là như nhau. Ta nói chúng đồngkhả năng Open. Vậy năng lực Open của mỗi mặt làDo đó, nếu A là biến cố : “ Con súc sắc Open mặt lẻ ” ( A = { 1,3,5 } ) thì năng lực xảy ra của A là1 1 1 3 1 ー + ー + ー = ー = ー 。 6 6 6 6 2 số này được gọi là xác suất của biến cốA. 5 – ĐAI SỐ và GLẢI TÍCH 11 – A 651 汽, một hộp chứa bốn quả cầu ghi chữa, hai quả cầu ghi chữ b và hai quả cầu ghi2. chữ C ( h. 34 ), lấy ngẫu nhiên một quả. Kí hiệu : A : “ Lấy được quả ghi chữa ” ; B : “ Lấy được quả ghi chữ b ” : C : “ Lấy được quả ghi chữ c ”. Có nhận xét gì về năng lực xảy ra của những biến cố A, B và C ? Hãy so sánh chúng Với nhau.lo O CO O G ) GED oolHình 34 Một cách tổng quát, ta có định nghĩa sau đây. ĐINH NGHIAGiả sử A là biến cố tương quan đến một phép thử chỉ có một sốhữu hạn tác dụng đồng năng lực Open. Ta gọi tỉ số 器 là xác suất của biến cố4, kí hiệu là P ( A ). P ( A ) = n ( A ). η ( Ω ) CHÚ Ýn ( A ) là số thành phần của A hay cũng là số những hiệu quả thuận tiện chobiến cố A, còn n ( O ) là số những tác dụng hoàn toàn có thể xảy ra của phép thử. Ví dụVí dụ 2. Gieo ngẫu nhiên một đồng xu tiền cân đối và đồng chất hai lần. Tính xác suất của những biến cố sau : a ). A. : “ Mặt sấp Open hai lần ” ; b ) B : “ Mặt sấp Open đúng một lần ” ; c ) C : “ Mặt sấp Open tối thiểu một lần ”. 5 – ĐAI SỐ và G | ẢI TÍCH 11 – BGiải ( h. 35 ). Không gian mẫu Q = { SS, SN, NS, NN } gồm bốn hiệu quả. Vì đồng xu tiền cân đối, đồng chất và 5.55 W việc gieo là ngẫu nhiên nên những hiệu quả đồng năng lực Open. Ta có * NS * NN. a ). A = { SS }, n ( A ) = 1, n { 6 } ) = 4, theo định nghĩa ta có P ( A ) = PA =. Hình 35 n ( C2 ) 4 b ) B = { SW, NS }, m ( B ) = 2 nên PB ) = IP = 2 = 1 n ( 2 ) 4 2 c ) C = { SS, SN, NS }, n ( C ) = 3 nên P ( C ) = n ( C ) 3. n ( Q. ) 4V í dụ 3. Gieo ngẫu nhiên một con súc sắc cân đối và đồng chất. Tính xác suất của những biến cố sau : A : “ Mặt chẵn Open ” ; B ’ : “ Xuất hiện mặt có số chấm chia hết cho 3 ” : C ’ : “ Xuất hiện mặt có số chấm không bé hơn 3 ” … . : : :: / / ình 36 Giải. Không gian mẫu có dạng : { } = { 1, 2, 3, 4, 5, 6 }, gồm sáu tác dụng đồng năng lực Open ( h. 36 ). Rõ ràng A = { 2, 4,6 }, n ( A ) = 3, B = { 3,6 }, n ( B ) = 2, C = { 3,4,5,6 }, n ( C ) = 4. Từ đó, theo định nghĩa ta cóPB ) = IP = 2 =, ( Ω ) 6 3PC ) = 2 = – 2. n ( ( ) ) 6 3V í dụ 4. Gieo ngẫu nhiên một con súc sắc cân đối và đồng chất hai lần. Tính Xác suất của những biến cố sau : 4 : “ Số chấm trong hai lần gieo bằng nhau ” ; B : “ Tổng số chấm bằng 8 ”. Giải. Như đã biết ( xem Ví dụ 3, S4 ), C2 = { ( i, j ) | 1 < i, j < 6 }, gồm 36 tác dụng đồng năng lực Open. Ta có bảng ( xem thêm Hình 29 ) : A = { ( 1,1 ), ( 2, 2 ), ( 3, 3 ), ( 4, 4 ), ( 5,5 ), ( 6, 6 ) }, n ( A ) = 6, n ( ( ) ) = 36. Từ đó, theo định nghĩa ta cóP ( A ) = " A = 0 = n ( ( ) ) 36 6. Tương tự, B = { { 2, 6 ), ( 6, 2 ), ( 3,5 ), ( 5,3 ), ( 4,4 ) }, n ( B ) = 5, n ( O ) = 36 nên P ( B ) = n ( B ) 5 π ( Ω ) 36II - TÍNH CHẤT CỦA XÁC SUẤT 1. Định líGiả sử A và B là những biến cố tương quan đến một phép thử có 1 số ít hữu hạn tác dụng đồng năng lực Open. Khi đó, ta có định lí sau đây. 2. ĐINH Lía ) P ( 2 ) = 0, P ( O ) = 1. b ) 0 < P ( A ) < 1, với mọi biến cố A.c ). Nếu A và B xung khắc, thì P ( A \ _J B ) = P ( A ) + P ( B ) ( công thức cộng xác suất ). 2 Chứng minh những tính chấta ), b ) và C ). HÊ QUẢVới mọi biến cố A, ta có P ( A ) = 1 - P ( A ). Chứng minh. Vì A \ _J A = Q và Air A = 2 nên theo công thức cộng xác suất ta có1 = P ( a ) = P ( A ) + P ( A ). Từ đó ta có điều phải chứng tỏ. = Ví dụVí dụ 5. Từ một hộp chứa ba quả cầu trắng, hai quả cầu đen ( h. 37 ), lấy ngẫu nhiên đồng thời hai quả. Hãy tính xác O O O O O suất sao cho hai quả đó : a ) Khác màu : b ) Cùng màu. Hình 37 Giải. Mỗi lần lấy đồng thời hai quả cầu cho ta một tổng hợp chập hai của năm thành phần. Do đó, khoảng trống mẫu gồm những tổng hợp chập hai của năm thành phần và n ( O ) = C = 10. Vi việc lấy quả cầu là ngẫu nhiên nên những hiệu quả đó đồng năng lực. Kí hiệu A. : " Hai quả khác màu ", B : " Hai quả cùng màu ". Vì chỉ có hai màu đen hoặc trắng nên ta thấy ngay B = A '. a ) Theo quy tắc nhân, n ( A ) = 3. 2 = 6.70 Do đób ) ViB = A nên theo hệ quả ta cóP ( B ) = P ( A ) = 1 - P ( A ) = i. Ví dụ 6. Một hộp chứa 20 quả cầu đánh số từ 1 đến 20. Lấy ngẫu nhiên một quả. Tính xác suất của những biến cố sau : a ). A. : " Nhận được quả cầu ghi số chẵn " ; b ) B : " Nhận được quả cầu ghi số chia hết cho 3 ; c ) Ary B ; d ) C : " Nhận được quả cầu ghi số không chia hết cho 6 ". Giải Không gian mẫu được miêu tả là { } = { 1, 2, ..., 20 } gồm 20 tác dụng đồng năng lực, m ( G ) = 20. a ). A = { 2,4, 6, 8, 10, 12, 14, 16, 18, 20 }, n ( A ) = 10 nênn ( A ) 10 1 A ) = - ܒ -- ܒ --. " = 話-新一主 b ) B = 3, 6, 9, 12, 15, 18, n ( B ) = 6. Từ đó Pb = ° 一皇一孚 η ( Ω ) 20, 10 c ). Vì Air, B = { 6, 12, 18 } ... n { A r \ B } = 3 nên P ( A C B ) = TA CP ) = 3. n ( ( ) ) 20 d ). Vì Air B = { 6, 12, 18 }, nên Air B là biến cố : " Nhận được quả cầu ghi số chia hết cho 6 ". Do đó, C là biến cố đối của biến cố A ^ B, ta có C = A r \ B và3 17 P ( C ) = 1 - P ( An B ) = 1 - - - - - -. ( C ) ( 4 nB ) 20 20III - CÁC BIÊN CỐ Độ. C LÂP, CÔNG THỨC NHÂN XÁC SUẤTVí dụ 7. Bạn thứ nhất có một đồng xu tiền, bạn thứ hai có con súc sắc ( đều cân đối, đồng chất ). Xét phép thử " Bạn thứ nhất gieo đồng xu tiền, sau đó bạnthứ hai gieo con súc sắc " ( h. 38 a ). a ). Mô tả khoảng trống mẫu của phép thử này. b ) Tính xác suất của những biến cố sau : A : " Đồng tiền Open mặt sấp " ; B : " Con súc sắc Open mặt 6 chấm " ; C : " Con súc sắc Open mặt lẻ ". c ) Chứng tỏ P ( A, B ) = P ( A ) P ( B ) ; P ( A.C ) = P ( A ) P ( C ). Giaiia ) Không gian mẫu của phép thử có dạngഗ ് ഗ ീ ( ) = ( S1, S2, S3, S4, S5, S6, N1, N2, N3, N4, N5, N6 }. / S ། ། 4. Theo giả thiết, ( ) gồm 12 tác dụng đồng năng lực N 5 Open ( h. 38 b ). 6 1 Z 2 ഗ ് ഗ ീ 3. NN 4. a ) b ) N 5 Hinih 38 6 b ) Ta thấy A = { USD 1, USD 2, S3, S4, USD 5, USD 6 }, n ( A ) = 6 ; B = S6, N6 ), n ( B ) = 2 ; C = N1, N3, N5, S1, S3, S5 ), n ( C ) = 6. Từ đó P ( A ) = = - n ( ( ) ) 12 2 P ( b ) = IP = i = ) ; n ( ( ) ) 12 6 Pic ) = - - η ( Ω ) 12 2S1 S2N1 N2 N3 N4 N5 N6 A.B ) 1 Rõ ràng A, B = IS6 ) và P ( A, B ) = ( * * ) = +. c ) Rõ ràng { USD 6 } và P ( A, B ) n ( ( ) ) 12 Ta có P ( AB ) = 1 = 1 = P ( A ) P ( b ) ' ' 12 26 - Tương tự, A.C = { S1, S3, S5 } : PAC ) = “ ) = = = = PA ) PC ) = η ( Ω ) 12 4 22T rong Ví dụ 7, ta nhận thấy xác suất Xuất hiện mỗi mặt của con súc sắc là không phụ thuộc vào vào việc đồng xu tiền Open mặt " sấp " hoặc " ngửa ". Nếu sự xảy ra của một biến cố không tác động ảnh hưởng đến xác suất xảy ra của một biến cố khác thì ta nói hai biến cố đó độc lập. Như vậy, trong Ví dụ 7, những biến cố A và B độc lập và cũng vậy, A và C độc lập. Tổng quát, so với hai biến cố bất kể ta có mối quan hệ sau : A và B là hai biến cố độc lập khi và chỉ khi P ( AB ) = P ( A ). P ( B ). B Ả I ĐQ C TH Ê MMỞ RÔNG QUY TÁC CÔNG VA CÔNG THỨC CÔNG XÁC SUẤTQuy tắc cộng còn được lan rộng ra so với những tập hợp hữu hạn, có giao khác rỗng. Có thể chứng tỏ được rằng, với hai tập hợp hữu hạn A và B bất kể, ta có n ( A \ _ B ) = n ( A ) + n ( B ) – n ( Air B ) ( quy tắc bao hàm và loại trừ ). Ví dụ 1. Một tổ mười người sẽ được chơi hai môn thể thao là cầu lông và bóng bàn. Có năm bạn đăng kí chơi cầu lông, bốn bạn đăng kí chơi bóng bàn, trong đó Có hai bạn đăng kí chơi cả hai môn. Hỏi có bao nhiêu bạn đăng kí chơi thể thao ? Bao nhiêu bạn không đăng kí chơi thể thao ? Giải. Kí hiệu X là tập hợp những học viên trong tổ ; A là tập hợp những học viên đăng kí chơi cầu lông, B là tập hợp những học viên đăng kíchơi bóng bàn ( h. 39 ), thế thì n ( x ) = 10, n ( A ) = 5, n ( B ) = 4, n ( Air B ) = 2. Như vậy : A J. B là tập hợp những bạn đăng kí chơi thể thao. Vì n ( Air B ) = 2 nên số bạn đăng kí chơi thể thao là n ( A \ J B ) = n ( A ) + n ( B ) – n ( Air B ) = 5 + 4 – 2 = 7 ( bạn ). Từ đó, số bạn không đăng kí chơi môn thể thao nào là / / ình 39 n ( X ) – n ( A \ _ B ) = 10 – 7 = 3 ( bạn ), m Nhờ quy tắc cộng lan rộng ra, ta có công thức cộng xác suất lan rộng ra sau đây. Với hai biến cố A và B bất kì cùng tương quan đến một phép thử, P ( Au B ) = P ( A ) + P ( B ) - P ( A, B ). Ví dụ 2. Gieo ngẫu nhiên một con súc sắc cân đối đồng chất hai lần. Tính xác suất của những biến cố sau : : " Lần thứ nhất Open mặt 6 chấm " : : " Lần thứ hai Open mặt 6 chấm " : : " Ít nhất một lần Open mặt 6 chấm " ; D : " Không lần nào Open mặt 6 chấm ", Giải. Ta có Q = { { i, j ) | | < i, j < 6 ), trong đó f là số chấm Open trong lần gieo thứ nhất, j là số chấm Open trong lần gieo thứ hai, n ( O ) = 36. Như vậy A = { ( 6, j ) 1 < j < 6 }, n ( A ) = 6 ; B = { ( i., 6 ) 1 < t < 6 ), n ( B ) = 6 ; C = Au B, D = C, Air B = { ( 6, 6 ), n ( An B ) = 1. Từ đó, theo định nghĩa ta cóP ( A ) = " A = 0 = P ( b ) = IP = 0 = l, η ( Ω ) 36 6 η ( Ω ) 36 6 P ( AB ) = " 4 CP ) — l. n ( C2 ) 36T heo nhận xét ta có | 1 | 11 P ( C ) = P ( AUB ) = P ( A ) + P ( B ) - P ( A, B ) = + --- - - - -. ( C ) = P ( Au B ) = P ( A ) + PB ) - PA, B ) = = Theo hệ quả ta có 1 25 P ( D ) = P ( C ) = 1 - P ( C ) = 1 - - - - T. ( D ) = P ( C ) P ( C ) 36 36 1.2.3. 4.5.6. Bởi tập Gieo ngẫu nhiên một con súc sắc cân đối và đồng chất hai lần. a ). Hãy miêu tả khoảng trống mẫu. b ). Xác định những biến cố sau : A : " Tổng số chấm Open trong hai lần gieo không bé hơn 10 " ; B : " Mặt 5 chấm Open tối thiểu một lần ". c ) Tính P ( A ), P ( B ). Có bốn tấm bìa được đánh số từ 1 đến 4. Rút ngẫu nhiên ba tấm. a ). Hãy miêu tả khoảng trống mẫu. b ). Xác định những biến cố sau : A : " Tổng những số trên ba tấm bìa bằng 8 " : B : " Các số trên ba tấm bìa là ba số tự nhiên liên tục ". c ) Tính P ( A ), P ( B ). Một người chọn ngẫu nhiên hai chiếc giày từ bốn đôi giày cỡ khác nhau. Tính xác suất để hai chiếc chọn được tạo thành một đôi. Gieo một con súc sắc cân đối và đồng chất. Giả sử con súc sắc Open mặt b chấm. Xét phương trình x ° + bx + 2 = 0. Tính xác suất sao cho : a ) Phương trình có nghiệm : b ) Phương trình vô nghiệm : c ) Phương trình có nghiệm nguyên, Từ cỗ bài tú lơ khơ52 con, rút ngẫu nhiên cùng một lúc bốn con. Tính xác suất sao cho : a ) Cả bốn con đều là át ; b ) Được tối thiểu một con át : c ) Được hai con át và hai con K. Hai bạn nam và hai bạn nữ được xếp ngồi ngẫu nhiên vào bốn ghế xếp thành hai dãy đối lập nhau. Tính xác suất sao cho : a ) Nam, nữ ngồi đối lập nhau : b ). Nữ ngồi đối lập nhau. 7. Có hai hộp chứa những quả cầu. Hộp thứ nhất chứa 6 quả trắng, 4 quả đen. Hộp thứ hai chứa 4 quả trắng, 6 quả đen. Từ mỗi hộp lấy ngẫu nhiên một quả. Kí hiệu : A là biến cố : " Quả lấy từ hộp thứ nhất trắng " : B là biến cố : " Quả lấy từ hộp thứ hai trắng ". a ). Xét xem A và B có độc lập không. b ) Tính xác suất sao cho hai quả cầu lấy ra cùng màu. c ) Tính xác suất sao cho hai quả cầu lấy ra khác màu. B Ả I ĐQ C TH Ê MĐịNH NGHÎA THỐNG KÊ CỦA XÁC SUẤTMột đồng tiên cân đối và đồng chất được gieo n lần. Kí hiệu n là số lần Open mặt sấp S trong n lần gieo đó, Ta gọi tỉ số f ( S ) = 竺郎 tần suất Open mặt sấp trong n lần gieo. Bằng thực nghiệm ta thấy, tần suất biến hóa khi ta thực thi loạt n lần gieo khác cũng như khi tăng số lần gieo. Tuy nhiên với n khá lớn, tần suất này có tính không thay đổi, nghĩa là nó xê dịch xung quanh số và khi n tăng, tần suất ngày càng gần sốTa hoàn toàn có thể tưởng tượng điều đó qua bảng những hiệu quả gieo đồng tiền của những nhà toán học Buýp-phông ( Buffont ) và Piếc-sơn ( Pearson ) sau đây. Người gieo Số lần gieo Số lần Open mặt S Tần suất Buyp-phong 4040 2048 0.5069 Piéc-son 2000 6019 0.5016 Piec-son 24000 2012 0,500. 5S ő mà tần suất f ( S ) xê dịch quanh nó được gọi là xác suất của biến cố USD theo quan điểm thống kê, 75T rong trường hợp phép thử chỉ có một số ít hữu hạn hiệu quả đồng năng lực Open thì số P ( A ) trong định nghĩa này trùng với số P ( A ) trong định nghĩa cổ xưa của xác suất. Do đó, định nghĩa thống kê của xác suất là một sự lan rộng ra thực sự xác suất. của định nghĩa cổ xưa của xác s Nhà toán học Thuỵ Sĩ J. Béc-nu-li ( Jacob Bernoulli ) là người tiên phong phát hiện ratính không thay đổi thống kê của dãy tần suất 74. Poát-xóng ( Poi ) là ng ... a. .. . gọi quy l ậtổ định Củ ܥ ܶ ܩ ܘ ất là luật số lớnÔn tộp chương IIPhát biểu quy tắc cộng, cho ví dụ vận dụng. Phát biểu quy tắc nhân, cho ví dụ vận dụng. Phân biệt sự khác nhau giữa một chỉnh hợp chập k của n thành phần và một tổng hợp chập k của n thành phần. Có bao nhiêu số chẵn có bốn chữ số được tạo thành từ những chữ số 0, 1, 2, 3, 4, 5, 6 sao cho : a ) Các chữ số hoàn toàn có thể giống nhau ? b ) Các chữ số khác nhau ? Xếp ngẫu nhiên ba bạn nam và ba bạn nữ ngồi vào sáu ghế kê theo hàng ngang. Tìm xác suất sao cho : a ) Nam, nữ ngồi xen kẽ nhau : b ) Ba bạn nam ngồi cạnh nhau. Từ một hộp chứa sáu quả cầu trắng và bốn quả cầu đen, lấy ngẫu nhiên đồng thời bốn quả. Tính xác suấ " sao cho : a ). Bốn quả lấy ra cùng màu : b ) Có tối thiểu một quả màu trắng .

Source: http://139.180.218.5
Category: tản mạn